Author |
Topic: Liquid Lunch (Read 1052 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Liquid Lunch
« on: Jan 30th, 2009, 5:52pm » |
 Quote  Modify
|
Tom, Dick, and Harry were having a drink at lunchtime. But they must get back to the office 9 miles away by 3.00 pm. Tom has a bike, Dick has a moped, and Harry has no transport at all. So they decided to share. Each of them can walk at 5mph, cycle at 9mph, and ride the moped at 15mph. Although neither vehicle can take more than one person, they can be left safely by the road for somebody else. The three friends left the bar together at the last minute and arrived back just in time for work.
At what time did they leave the bar?
|
|
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
teekyman
Full Member
Gender:
Posts: 199
|
|
Re: Liquid Lunch
« Reply #1 on: Jan 30th, 2009, 11:29pm » |
Quote Modify
|
I can have them leaving at 1:52 and thats probably the optimum.
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Liquid Lunch
« Reply #2 on: Jan 31st, 2009, 2:33am » |
Quote Modify
|
I find the same.
How?
#1: ride 5 miles @ 15 mph = 20 min.
walk 4 miles @ 5 mph = 48 min.
total: 68 min.
#2: cycle 1.5 miles @ 9 mph = 10 min.
walk 3.5 miles @ 5 mph = 42 min.
ride 4 miles @ 15 mph = 16 min.
total: 68 min.
#3: walk 1.5 miles @ 5 mph = 18 min.
cycle 7.5 miles @ 9 mph = 50 min.
total: 68 min.
|
| « Last Edit: Feb 1st, 2009, 8:37am by Grimbal » |
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Liquid Lunch
« Reply #3 on: Jan 31st, 2009, 6:32am » |
Quote Modify
|
At a later date Tom, Dick, and Harry decide to go for lunch at a local bistro 10 miles from their office. Dick's moped can still do 15mph, they still walk at 5mph, and Harry still has no transport of his own. But Tom's bike has been damaged and, as it can now do no more than 6mph, he doesn't care what happens to it. As before, they leave the bistro together at the last minute and arrive back just in time for work.
At what time did they leave the bistro?
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
teekyman
Full Member
Gender:
Posts: 199
|
|
Re: Liquid Lunch
« Reply #4 on: Jan 31st, 2009, 10:47pm » |
Quote Modify
|
As before, the theoretical limit is found by considering that every vehicle must make the journey at least once, which will need, in this case, 9/5 + 9/6 + 9/15 = 3.9 man-hours, thus at best we can have each person take 1.3 hours. However, I'm having much more difficulty gerrymandering them all in, probably for some important reason.
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Liquid Lunch
« Reply #5 on: Feb 1st, 2009, 1:06am » |
Quote Modify
|
on Jan 31st, 2009, 10:47pm, 1337b4k4 wrote:| However, I'm having much more difficulty gerrymandering them all in, probably for some important reason. |
|
Indeed, as they must now travel 10 miles. 
So try shoehorning them into 260/3 mins.
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Immanuel_Bonfils
Junior Member
Posts: 114
|
|
Re: Liquid Lunch
« Reply #6 on: Mar 1st, 2009, 8:41pm » |
Quote Modify
|
Assume n persons traveling the total distance n*d with n-1 vehicles and by foot, on n different speeds, without stopping.
For which values of n can they do it with each vehicle traveling distance d?
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Liquid Lunch
« Reply #7 on: Mar 23rd, 2009, 7:51am » |
Quote Modify
|
on Mar 1st, 2009, 8:41pm, Immanuel_Bonfils wrote:Assume n persons traveling the total distance n*d with n-1 vehicles and by foot, on n different speeds, without stopping.
For which values of n can they do it with each vehicle traveling distance d? |
|
Let L = the length of the journey
Let M = the number of travellers
Let N = the number of vehicles
Let T = the time time taken by the last traveller to arrive at the destination
Let v0 = the speed with which they travel on foot
Let vr = the speed of the rth vehicle (r = 1 to N - 1)
Then
t0 = L/v0
t1 = L/v1
t2 = L/v2
t1 = L/v3
If there were no vehicles available, the total of the times taken by the M travellers would be Mt0.
Making one vehicle available with speed vr can reduce this total by at most t0 - tr.
Making N vehicles available reduces this total by at most (t0 - t1) + (t0 - t2) + (t0 - t3) + ........ + (t0 - tN)
That is, the total time for M travellers using N vehicles is at least (M - N)t0 + t1 + t2 + t3 + ........ + tN
Let T* = [(M - N)t0 + t1 + t2 + t3 + ........ + tN]/M
Then we have T 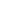 T* where T is the time taken by the last traveller to arrive at the destination.
Also, if T = T* then every traveller takes T* to arrive at the destination, as T* is the average time they take and T is the time taken by the last arrival. That is, T = T* when t1,t2,t3,........,tN 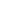 T* because, when no vehicles are abandoned, if any vehicle takes more than T* to complete the journey then its last user must also take more than T*.
In the first problem
L = 9
v0 = 5
v1 = 15
v2 = 9
t0 = 108
t1 = 36
t2 = 60
Hence T* = [108*(3 - 2) + 36 + 60]/3 = 68mins.
As t1 and t2 are both less than T*we have T = T*
In the second problem
L = 10
v0 = 5
v1 = 15
v2 = 6
t0 = 120
t1 = 40
t2 = 100
Hence T* = [120*(3 - 2) + 40 + 100]/3 = 86.666... mins.
But as t2 > T* we have T > T* and there is no 'easy' solution.
But they are allowed to abandon a vehicle, the bike. Suppose they abandon the bike after D miles from the start, taking 10D minutes, and ride the rest of the way using the moped left by the others, taking 4(10 - D) minutes. So total time = 10D + 4(10 - D) = 6D + 40 minutes. The other two will have cooperated to get the moped to the dropping-off point, each riding D/2 miles and walking D/2 miles, and then walking together to the destination, taking a further 12(10 - D) = 120 - 4D miles.
So the last of these three to arrive will have taken max{6D + 40, 120 - 4D}
This is minimised when the two amounts are equal. That is, when D = 8
Putting D = 8 gives T = 88 minutes as the common time for all travellers to arrive.
|
| « Last Edit: Mar 23rd, 2009, 11:31am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print