Author |
Topic: Committees (Read 1988 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
The population of Evenville form committees according to the following rules:
1) There must be an EVEN number of members in each committee.
2) Any two committees must share an EVEN number of members.
3) No pair of committees can have identical membership.
The population of Oddville have the following rules:
1) There must be an ODD number of members in each committee.
2) Any two committees must share an EVEN number of members.
Evenville has a population of just 20 while Oddville's population is 1000. How is it possible that, although Oddville tries to form as many committees as possible according to its own rules, it still has less committees than Evenville?
|
|
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
 |
Re: Committees
« Reply #1 on: Jan 24th, 2009, 7:59am » |
 Quote  Modify
|
Does Evenville have the empty committee?
Immediate thoughts show that Evenville can have at least 1023 committees (or 1024 with the empty committee) pair up the citizens, so that each is on precisely those committees his partner is, and form the power set of that set of pairs
Intuitively, it looks like any Oddville with population n can have at most n committees, but I've got nothing like a proof.
An interesting, if trivial and possibly unhelpful, observation is that Oddville can't have any subcommittees.
Attempting to prove the n committees result by induction, it's trivial in the case where the committees can be partitioned into non-overlapping sub-towns, but I've got nowhere with the remaining case.
It's easy to show that, when Oddville has the maximum number of committees, each citizen, A, must be on at least one committee (otherwise, you can add the new committee {a}), and that, for each pair of citizens, A,B, there must be at least one committee with one but not the other - if they always appear together or not at all, you can pull them from all committees (those where they both appeared still have an odd number of members and have lost 2 from their pairwise intersections with each other, while the committees that had neither as members have no change in membership nor in intersection with any other committee) and add {A} and {B}
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Committees
« Reply #2 on: Jan 27th, 2009, 11:41pm » |
Quote Modify
|
on Jan 24th, 2009, 7:59am, rmsgrey wrote:Does Evenville have the empty committee?
|
|
Yes, being no less effective, empty committees are admissible.
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Committees
« Reply #3 on: Apr 16th, 2009, 6:08pm » |
Quote Modify
|
Hint: Linear algebra
|
|
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Committees
« Reply #4 on: Apr 22nd, 2009, 1:04pm » |
Quote Modify
|
Another hint, following up on Eigenray's hint: Linear Independence
|
|
IP Logged |
|
|
|
Peterman
Newbie
Posts: 7
|
|
Re: Committees
« Reply #5 on: May 6th, 2009, 7:25am » |
Quote Modify
|
Useful hint! Represent a committee drawn from a population of size N as an N-dimensional vector of 0s and 1s, 1 indicating membership.
Then:
the key point is that in Z2, an inner product of two such vectors is always just the parity of the intersection of the two. The inner product of an OddTown committee with itself is 1 because it has an odd number of members, whereas the inner product of two different committees is zero, since the intersection is even. Thus all OddTown committees are orthogonal and independent, so there can be at most N of them.
Great puzzle -- really kept me awake some nights!
Followup thought: There are lots of possible ways to construct N committees in OddTown. If N is even, one way is N singletons, another is N committess each leaving just one person out. And of course you can partition the N into even subsets and make either choice for each subset. If N is odd you can extract one person to be a singleton committee and then split the N-1 into committees in lots of ways as just described. Does this process generate all the possibilities?
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Committees
« Reply #6 on: May 7th, 2009, 3:04am » |
Quote Modify
|
on May 6th, 2009, 7:25am, Peterman wrote:| Followup thought: There are lots of possible ways to construct N committees in OddTown. If N is even, one way is N singletons, another is N committess each leaving just one person out. And of course you can partition the N into even subsets and make either choice for each subset. If N is odd you can extract one person to be a singleton committee and then split the N-1 into committees in lots of ways as just described. Does this process generate all the possibilities? |
|
If I understand you correctly, this would give 17 possibilities for the case n=6:
1 way in which each committee has 1 member
1 way in which each committee has 5 members
15 = C(6,4) ways in which 4 committees have 3 members, and 2 committees have 1.
But there are actually 32 ways: see A088437 and A003053. For the proof, MacWilliams notes that A 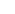 AAt gives a bijection from right cosets of the orthogonal group O(n,2) in GL(n,2), to invertible matrices which can be written in the form AAt. He shows that an invertible symmetric matrix can be written in this form iff its diagonal contains at least one non-zero entry, and then he counts the number of such matrices.
|
|
IP Logged |
|
|
|
Peterman
Newbie
Posts: 7
|
|
Re: Committees
« Reply #7 on: May 8th, 2009, 5:17am » |
Quote Modify
|
on May 7th, 2009, 3:04am, Eigenray wrote:
If I understand you correctly, this would give 17 possibilities for the case n=6:
1 way in which each committee has 1 member
1 way in which each committee has 5 members
15 = C(6,4) ways in which 4 committees have 3 members, and 2 committees have 1.
But there are actually 32 ways: see A088437 and A003053. For the proof, MacWilliams notes that A 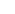AAt gives a bijection from right cosets of the orthogonal group O(n,2) in GL(n,2), to invertible matrices which can be written in the form AAt. He shows that an invertible symmetric matrix can be written in this form iff its diagonal contains at least one non-zero entry, and then he counts the number of such matrices. |
|
Hmm, then what are the missing 15 ways? So far we
are talking about these 17 possible sets of 6 committees:
| 01: | a, | b, | c, | d, | e, | f | | 02: | abc, | abd, | acd, | bcd, | e, | f | | 03: | abc, | abe, | ace, | bce, | d, | f | | 04: | abc, | abf, | acf, | bcf, | d, | e | | 05: | abd, | abe, | ade, | bde, | c, | f | | 06: | abd, | abf, | adf, | bdf, | c, | e | | 07: | abe, | abf, | aef, | bef, | c, | d | | 08: | acd, | ace, | ade, | cde, | b, | f | | 09: | acd, | acf, | adf, | cdf, | b, | e | | 10: | ace, | acf, | aef, | cef, | b, | d | | 11: | ade, | adf, | aef, | def, | b, | c | | 12: | bcd, | bce, | bde, | cde, | a, | f | | 13: | bcd, | bcf, | bdf, | cdf, | a, | e | | 14: | bce, | bcf, | bef, | cef, | a, | d | | 15: | bde, | bdf, | bef, | def, | a, | c | | 16: | cde, | cdf, | cef, | def, | a, | b | | 17: | abcde, | abcdf, | abcef, | abdef, | acdef, | bcdef |
What am I missing?
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Committees
« Reply #8 on: May 8th, 2009, 5:58am » |
Quote Modify
|
By brute force:
Code:
U = Select[IntegerDigits[Range[0,2^6-1],2,6], Mod[#.#,2]==1&];
p[S_, v_] := Select[S, Order[v, #]>0 && Mod[#.v,2]==0 &];
f[B_, S_] := If[Length@B==6, Sow@B, f[Append[B,#],p[S,#]]&/@S];
Reap[f[{},U]][[2,1]];
|
|
{000001,000010,000100,001000,010000,100000}
{000001,000010,011100,101100,110100,111000}
{000001,000100,011010,101010,110010,111000}
{000001,001000,010110,100110,110010,110100}
{000001,001110,010000,100110,101010,101100}
{000001,001110,010110,011010,011100,100000}
{000010,000100,011001,101001,110001,111000}
{000010,001000,010101,100101,110001,110100}
{000010,001101,010000,100101,101001,101100}
{000010,001101,010101,011001,011100,100000}
{000100,001000,010011,100011,110001,110010}
{000100,001011,010000,100011,101001,101010}
{000100,001011,010011,011001,011010,100000}
{000111,001000,010000,100011,100101,100110}
{000111,001000,010011,010101,010110,100000}
{000111,001011,001101,001110,010000,100000}
{000111,001011,010011,100011,111101,111110}
{000111,001101,010101,100101,111011,111110}
{000111,001110,010110,100110,111011,111101}
{001011,001101,011001,101001,110111,111110}
{001011,001110,011010,101010,110111,111101}
{001101,001110,011100,101100,110111,111011}
{010011,010101,011001,101111,110001,111110}
{010011,010110,011010,101111,110010,111101}
{010101,010110,011100,101111,110100,111011}
{011001,011010,011100,101111,110111,111000}
{011111,100011,100101,101001,110001,111110}
{011111,100011,100110,101010,110010,111101}
{011111,100101,100110,101100,110100,111011}
{011111,101001,101010,101100,110111,111000}
{011111,101111,110001,110010,110100,111000}
{011111,101111,110111,111011,111101,111110}
[ Corrected -- thanks rmsgrey ]
|
| « Last Edit: May 10th, 2009, 9:16am by Eigenray » |
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: Committees
« Reply #9 on: May 9th, 2009, 2:28pm » |
Quote Modify
|
on May 8th, 2009, 5:17am, Peterman wrote:
Hmm, then what are the missing 15 ways? So far we
are talking about these 17 possible sets of 6 committees:
| 01: | a, | b, | c, | d, | e, | f | | 02: | abc, | abd, | acd, | bcd, | e, | f | | 03: | abc, | abe, | ace, | bce, | d, | f | | 04: | abc, | abf, | acf, | bcf, | d, | e | | 05: | abd, | abe, | ade, | bde, | c, | f | | 06: | abd, | abf, | adf, | bdf, | c, | e | | 07: | abe, | abf, | aef, | bef, | c, | d | | 08: | acd, | ace, | ade, | cde, | b, | f | | 09: | acd, | acf, | adf, | cdf, | b, | e | | 10: | ace, | acf, | aef, | cef, | b, | d | | 11: | ade, | adf, | aef, | def, | b, | c | | 12: | bcd, | bce, | bde, | cde, | a, | f | | 13: | bcd, | bcf, | bdf, | cdf, | a, | e | | 14: | bce, | bcf, | bef, | cef, | a, | d | | 15: | bde, | bdf, | bef, | def, | a, | c | | 16: | cde, | cdf, | cef, | def, | a, | b | | 17: | abcde, | abcdf, | abcef, | abdef, | acdef, | bcdef |
What am I missing? |
|
With an even population, for any legal set of committees, the set of complementary committees is also legal.
Proof:
1) Each committee has an odd number of members. Therefore the complement of any given committee must also have an odd number of members since the two include the entire population precisely once, for an even total.
2) For any two committees with an even intersection, the number of members in the union must be even (sum of the two committees' sizes less the size of the intersection - odd+odd-even=even) so the intersection of the complements - the people in neither committee - being the complement of the union, must also be even since the total population is.
In your list, 1 and 17 are complementary, so the other 15 are the complements of 2-16 - two committees of 5 and four committees of three (the two missing from each of the 5s and any other)
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: Committees
« Reply #10 on: May 9th, 2009, 2:33pm » |
Quote Modify
|
on May 8th, 2009, 5:58am, Eigenray wrote:{000001,001110,010110,011010,011100,100000}
{000001,001110,010110,011010,100000,011100}
{000001,001110,010110,100000,011010,011100}
|
|
I don't understand your code sufficiently well to debug it, but the three towns quoted (4th through 6th in the original list) have the same 6 committees listed in different orders.
There are other duplications in the list - this is merely the first. What tipped me off was the excessive number of towns starting 000111 - there should only be 6
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Committees
« Reply #11 on: May 10th, 2009, 9:15am » |
Quote Modify
|
on May 9th, 2009, 2:33pm, rmsgrey wrote:
I don't understand your code sufficiently well to debug it, but the three towns quoted (4th through 6th in the original list) have the same 6 committees listed in different orders.
|
|
Whoops! The solution was fine but I was using the FromDigits function to format the output so I could display the the vectors as numbers instead of lists of 0s and 1s. But apparently, if L is a list of n m-element lists, i.e., an n x m matrix, then FromDigits[L] is a list of the m n-digit numbers you get from reading the columns, not the n m-digit numbers you get from the rows. Since I had lists of 6 6-digits numbers I didn't notice. So I needed a transpose:
Code:
PaddedForm[FromDigits/@Transpose/@Reap[f[{},U]][[2,1]], 6, NumberPadding->"0", NumberSigns->{"",""}] |
|
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print