Author |
Topic: coin placing (Read 650 times) |
|
cool_joh
Newbie
Gender: 
Posts: 50
|
 |
coin placing
« on: Dec 17th, 2008, 5:20pm » |
 Quote  Modify
|
We have 111 coins. They are to be placed in unit cells of the table n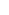 n so that the number of coins in any two neighboring (i.e. sharing a common side) cells differs exactly by 1 (a cell may contain several coins and may be empty, too). For which maximal n is this possible?
|
|
 IP Logged |
MATH PRO
|
|
|
aicoped
Junior Member
Gender:
Posts: 57
|
|
Re: coin placing
« Reply #1 on: Dec 17th, 2008, 9:30pm » |
Quote Modify
|
The answer is odd. It has no solutions for an even number square.
And trivially it can be done for a 1x1 square.
It can be done for 3x3 with 13 on the 4 corners and 12 on the four "sides" with 11 in the middle.
Five by five can be done. Imagine a checkerboard with all of the 13 squares that would be the same color as the center square equal to 5. And the rest are equal to 4. That answer will be too high by 2, so any corner instead of being 5 will be 3.
If I had to guess, I would suggest the answer is 13.
This is because for 15 square, it has 225 squares in it. And at least half of them must contain a 1, which would be 112, so 15 is impossible. And thirteen is theoretically possible, so It should not be to hard to actually fine the zeros ones and 2's that would make it work.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: coin placing
« Reply #2 on: Dec 18th, 2008, 1:42am » |
Quote Modify
|
on Dec 17th, 2008, 9:30pm, aicoped wrote:If I had to guess, I would suggest the answer is 13.
This is because for 15 square, it has 225 squares in it. And at least half of them must contain a 1, which would be 112, so 15 is impossible. And thirteen is theoretically possible, so It should not be to hard to actually fine the zeros ones and 2's that would make it work. |
|
Just start off with a checkerboard of zeroes and ones, (with ones in the corners), then replace an arbitrary 13 zeroes with twos.
(132+1)/2+2*13=111
Each zero and two is surrounded by ones, each one is surrounded by twos or zeroes.
You can find solutions for each smaller odd square in a similar way.
And for even numbers of coins there are solutions for both odd and even squares.
|
| « Last Edit: Dec 18th, 2008, 1:53am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
aicoped
Junior Member
Gender:
Posts: 57
|
|
Re: coin placing
« Reply #3 on: Dec 18th, 2008, 4:35am » |
Quote Modify
|
I realized that while lying in bed and hoped to post here before someone pointed thta out.
|
|
IP Logged |
|
|
|
cool_joh
Newbie
Gender:
Posts: 50
|
|
Re: coin placing
« Reply #5 on: Dec 18th, 2008, 5:28am » |
Quote Modify
|
LOL  You're correct, the answer is 13.
This problem is taken from Zhautykov Olympiad, an international mathematics olympiad held annually in Kazakhstan.
|
|
IP Logged |
MATH PRO
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print