 Author
Author |
Topic: Some subset has sum 60 (Read 498 times) |
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Some subset has sum 60
« on: Dec 7th, 2008, 10:52am » |
 Quote Quote  Modify Modify
|
You have 32 integers between 1 and 60 inclusive, whose total is 120. Show that some subset of these integers has sum 60.
|
|
 IP Logged IP Logged |
|
|
|
aicoped
Junior Member
 

Gender: 
Posts: 57
|
 |
Re: Some subset has sum 60
« Reply #1 on: Dec 9th, 2008, 11:59pm » |
 Quote Quote  Modify Modify
|
This is just using the pigeonhole method.
Basically, no matter which number you start with, you know you can't use it's "opposite half" so if the if you start with 1, then you can never use 59, etc, since there are only 29 complete halfs that total to 60, once you have used any of the 29 numbers you have excluded their other half. the only numbers left would be 30 which wouldn't have a half to match with and 60. So any number you picked after that would automatically mena that there is a 60 sum somewhere in your subsets.
Now, I notice you did not say distinct integers and if they could theoretically all be the same or more than one could be the same, as long as their total was 120, then I would have to think more on the problem.
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Some subset has sum 60
« Reply #2 on: Dec 10th, 2008, 5:31am » |
 Quote Quote  Modify Modify
|
It looks like the numbers can be repeated. If not, they couldn't sum to 120.
|
|
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Some subset has sum 60
« Reply #3 on: Dec 10th, 2008, 9:31am » |
 Quote Quote  Modify Modify
|
Some pairs of integers amongst the 32 must be equal. Since any 15 pairwise distinct positive integers sum to at least C(16,2)=120, there can be at most 14 pairwise distinct integers among 32 positive integers which sum to 120.
|
|
 IP Logged IP Logged |
|
|
|
aicoped
Junior Member
 

Gender: 
Posts: 57
|
 |
Re: Some subset has sum 60
« Reply #4 on: Dec 10th, 2008, 4:44pm » |
 Quote Quote  Modify Modify
|
Yes my bad, i realize now that 120 could not be reached with the other method. I was thinking that was one of those useless things they throw into problems to throw you off the right track.
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Some subset has sum 60
« Reply #5 on: Dec 12th, 2008, 12:20pm » |
 Quote Quote  Modify Modify
|
Surprisingly noone gives solution yet so I'll give my rather long proof.
We have 15m+2 numbers not exceeding 30m summing to 60m and want to proove there exists a subset summing to 30m (where m = 1 or 2).
Let number i appears in the list ni times. Encode list by (n1,...,n30m).
Suppose a counterexample exist. Than there exist the counterexample with lexicographically maximal encodding E=(n1,...,n30m).
1) n1+j is zero whenever j n1 and there are 2 other numbers k,l greater or equal j+1 summing less than 30m. n1 and there are 2 other numbers k,l greater or equal j+1 summing less than 30m.
Proof: Cutting 1 from j+1 and gluing k+l sum and count unchanged, and each newly obtainable sum was obtainable before therefore (n1+1,...,nj+1,n1+j-1,...,nk-1,...,nl-1,...,nk +l+1) is counterexample with bigger encodding.
(The only interesting cases are when the sum uses all nj j's and no 1 or it uses all n1 1's and no j, otherwise the split does not change the situation. As j n1, we can replace one j by j original 1's to obtain the same sum in the former case or j 1's by one j to obtain the same sum in the later case, so in both cases the split does not change the situation. On the other side joining k,l together may prevent some sums) n1, we can replace one j by j original 1's to obtain the same sum in the former case or j 1's by one j to obtain the same sum in the later case, so in both cases the split does not change the situation. On the other side joining k,l together may prevent some sums)
2) There exists i 3 and j 3 and j 4 such that ni 4 such that ni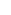 0 0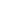 nj. nj.
Proof:For average hold 3 < 60m/(15m+2) = 4-8/(15m+2) < 4.
3) n1 1. 1.
Proof: Suppose k=n1>1. Let l be minimal number greater than 1 in the set. If k 15m-1, we can sum remaining numbers until any further summing leads to number greater than 30m. In that case at least one sum is at least 15m+1 so combined with ones gives sum 30m. 15m-1, we can sum remaining numbers until any further summing leads to number greater than 30m. In that case at least one sum is at least 15m+1 so combined with ones gives sum 30m.
So k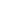 15m-1, there are at least 4 remaining numbers, if 2nd and third in size cannot be summed to get number less (or equal to) 30m, then sum of three bigest numbers must be at least 45m+2 so k 15m-1, there are at least 4 remaining numbers, if 2nd and third in size cannot be summed to get number less (or equal to) 30m, then sum of three bigest numbers must be at least 45m+2 so k  15m-4. If k 15m-4. If k  15m-4, there are at least 6 remaining numbers and 2 of five highest can be summed together to get less than 30m. So for k 15m-4, there are at least 6 remaining numbers and 2 of five highest can be summed together to get less than 30m. So for k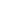 15m-1 according 1) l 15m-1 according 1) l k+2. We get 60m k+2. We get 60m  k+(15m+2-k)l k+(15m+2-k)l k+(15m+2-k)(k+2) = -k2+(15m+1)k+(30m+4). k2-(15m+1)k+(30m-4) k+(15m+2-k)(k+2) = -k2+(15m+1)k+(30m+4). k2-(15m+1)k+(30m-4)  0 gives |k-(15m+1)/2| 0 gives |k-(15m+1)/2|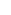 1/2 1/2 ((15m)2-3) ((15m)2-3)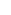 (15m-1)/2 so k (15m-1)/2 so k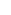 15m or k 15m or k 1. First case lead to contradiction so k 1. First case lead to contradiction so k 1. 1.
to be continued ...
|
| « Last Edit: Dec 12th, 2008, 12:29pm by Hippo » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Some subset has sum 60
« Reply #6 on: Dec 12th, 2008, 12:27pm » |
 Quote Quote  Modify Modify
|
4) n2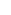 0 0
Proof: Suppose the contradiction, so the sum 60m is obtained by at most one 1, n3 3's and numbers above average.
Lexmin such configuration containing 1 is (1,0,5,15m-4,0,...) (without 1 the arguments would be simplified as we don't use it).
Maintaining the same sum we can simultaneously increment some number different from 3 and decrement one of 4's (both by 1). By such process we can get all remaining cases. If nj 3i for j 3i for j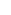 3, n3 3, n3 10m-1-ji, otherwise j's and 3's can be summed to 30m. So n3 10m-1-ji, otherwise j's and 3's can be summed to 30m. So n3 10m-1-4 10m-1-4 n4/3 n4/3 and as n4 and as n4 15m-4-2(n3-5)=15m+6-2n3 we obtain n3 15m-4-2(n3-5)=15m+6-2n3 we obtain n3 10m-1-20m-8+4 10m-1-20m-8+4 2n3/3 2n3/3 =-10m-9+4 =-10m-9+4 2/3n3 2/3n3 . So 10m+9 . So 10m+9 4 4 2n3/3 2n3/3 -n3 -n3 4(2n3+2)/3-n3=5n3/3+8/3 therefore n3 4(2n3+2)/3-n3=5n3/3+8/3 therefore n3 6m+19/5 and finaly n3 6m+19/5 and finaly n3 6m+4. 6m+4.
Assumption that for some j 4 nj 4 nj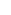 2 leads to 10m-1-j 2 leads to 10m-1-j n3 n3 6m+4, but as m 6m+4, but as m 2 we get 10m-1-j-6m-4 2 we get 10m-1-j-6m-4 4m-9 4m-9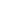 0 so there is no such n3 and we get contradiction. 0 so there is no such n3 and we get contradiction.
Therefore nj 2 whenever j 2 whenever j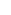 3. So at most two increment chains finish on 5, at most 2 on 6, ... the first such encoddings are (1,0,11,1,2,2,0,..) for m=1 and (1,0,31,2,2,2,2,1,2,0,..) for m=2. In both cases 3's can sum upto 30m. 3. So at most two increment chains finish on 5, at most 2 on 6, ... the first such encoddings are (1,0,11,1,2,2,0,..) for m=1 and (1,0,31,2,2,2,2,1,2,0,..) for m=2. In both cases 3's can sum upto 30m.
5) Suppose m=2, m'=m/2=1 ... divide the problem by 2  . By 1) we know n1=0. Take any pair of numbers of the same parity. As the sum of remaining 15m numbers is at least 30m, the sum of paired numbers does not exceed 30m. Make 15m' pairs and leave one of number's 2 and one other even number extra. After numbers are paired replace them by their sums. We got at least 2+15m' even numbers including number 2 among them summing to 60m. Divide each number by 2. We had 2+15m' numbers from 1,...,30m' with sum 60m' including number 1 among them asking to find subset with sum 30m'. Dividing encodding by 2 we get again lexmax encodding (n'1,...,n'30m'). . By 1) we know n1=0. Take any pair of numbers of the same parity. As the sum of remaining 15m numbers is at least 30m, the sum of paired numbers does not exceed 30m. Make 15m' pairs and leave one of number's 2 and one other even number extra. After numbers are paired replace them by their sums. We got at least 2+15m' even numbers including number 2 among them summing to 60m. Divide each number by 2. We had 2+15m' numbers from 1,...,30m' with sum 60m' including number 1 among them asking to find subset with sum 30m'. Dividing encodding by 2 we get again lexmax encodding (n'1,...,n'30m').
Accordind 1), 2), 3) and 4) applied to m' we get a contradiction as we get both n'2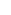 0 and n'1 0 and n'1 1. 1.
|
| « Last Edit: Dec 12th, 2008, 12:49pm by Hippo » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register