Author |
Topic: Two Intersecting Spheres (Read 490 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Two Intersecting Spheres
« on: Oct 21st, 2008, 3:00pm » |
 Quote  Modify
|
S and T, with radii r and R respectively, are two intersecting spheres such that S passes through the centre of T. If R 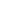 2r find the area of the surface of S that lies inside T.
|
|
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Two Intersecting Spheres
« Reply #1 on: Oct 21st, 2008, 3:48pm » |
Quote Modify
|
Surprising result, looks wrong at first, and yet it works.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Two Intersecting Spheres
« Reply #2 on: Oct 22nd, 2008, 1:45am » |
Quote Modify
|
Guessing, pi R2?
Works at 3 points, certainly.
R=0; quite obvious.
R=sqrt(2) r: 2 pi r2, half the sphere S.
R=2 r: 4 pi r2, whole sphere S.
|
| « Last Edit: Oct 22nd, 2008, 1:46am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Two Intersecting Spheres
« Reply #3 on: Oct 22nd, 2008, 6:21am » |
Quote Modify
|
Good guess, towr!
Let point O be the center of sphere S and point P be the center of sphere T. Take any plane passing through both O and P, and let point Q be one of the two points where S and T intersect in the plane. Triangle OPQ has sides of r, r and R, and so angle POQ has value  = 2sin-1(R/2r).
The surface area of S within T is then  0 2 r sin( ) r d
= 2r2 0 sin() d
= 2r2(1 - cos(2sin-1(R/2r)))
= 2r2(1 - (1 - 2sin2(sin-1(R/2r))))
= 4r2(R/2r)2
= R2
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print