Author |
Topic: Functional equation (Read 595 times) |
|
wonderful
Full Member
Posts: 203
|
 |
Functional equation
« on: Sep 2nd, 2008, 1:32pm » |
 Quote  Modify
|
Can you find f(x): R--> R such that
f(x+f(y)) = f(y+f(x)) for every x, y in R?
Have A Great Day!
|
|
 IP Logged |
|
|
|
pex
Uberpuzzler
Gender: 
Posts: 880
|
|
Re: Functional equation
« Reply #2 on: Sep 2nd, 2008, 2:18pm » |
Quote Modify
|
on Sep 2nd, 2008, 2:12pm, towr wrote:Very easily? f(x)=x
And of course f(x)=0 |
|
And both of these plus an arbitrary real constant.
At least, if there are other solutions, they cannot be injective:
| hidden: | Let f(x) be an injective solution.
Thus, f(x+f(y)) = f(y+f(x)) implies x+f(y) = y+f(x).
But then, for all x,y, f(x)-f(y) = x-y.
Or, for all x and y not equal, [f(x)-f(y)]/[x-y] = 1.
Taking the limit as y -> x, f'(x) exists and is equal to 1 for all x.
Thus, f(x) = x + constant. |
|
|
IP Logged |
|
|
|
wonderful
Full Member
Posts: 203
|
|
Re: Functional equation
« Reply #3 on: Sep 2nd, 2008, 2:42pm » |
Quote Modify
|
Great towr and pex! I also really like Pex's solution.
Have A Great Day!
|
|
IP Logged |
|
|
|
pex
Uberpuzzler
Gender:
Posts: 880
|
|
Re: Functional equation
« Reply #4 on: Sep 2nd, 2008, 2:54pm » |
Quote Modify
|
on Sep 2nd, 2008, 2:42pm, wonderful wrote:Great towr and pex! I also really like Pex's solution.
Have A Great Day! |
|
 I wouldn't consider this one solved yet...
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Functional equation
« Reply #5 on: Sep 2nd, 2008, 3:43pm » |
Quote Modify
|
Sure, pex proved the only injective solution is f(x) = x + C, but there are all kinds of non-injective solutions left to find!
towr notes f(x) = C as a trivial non-injective example. I'll also note f(x) =  x + D, D   and related families are solutions, as are f(x) = (x + C) mod m, m   0 and related families. I'm sure there are many more as well -- pretty much any function that maps  X 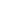 in a "periodic", "non-stretchy" way should work!
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: Functional equation
« Reply #6 on: Sep 3rd, 2008, 3:21pm » |
Quote Modify
|
Consider the following function:
f(x)=x if x is irrational
f(x)=0 if x is rational.
Then
f(x+f(y))=0 if x is rational and y is rational
f(x+f(y))=x if x is irrational and y is rational
f(x+f(y))=y if x is rational and y is irrational
f(x+f(y))=x+y if x is irrational, y is irrational, and x+y is irrational
f(x+f(y))=0 if x is irrational, y is irrational, and x+y is rational
from which it follows that f(x+f(y))=f(y+f(x)) in all cases. This gives a solution which is continuous at exactly 1 point.
This example can also be "composed" with SMQ's periodic examples, for instance by defining f(x) to be the remainder r of x with 0<= r < m after dividing by a rational (maybe irrational too, haven't thought enough about it) real number m whenever x is irrational and 0 otherwise.
More generally, if S is any subgroup of the real numbers under addition, it can take the place of the rationals in my construction.
For a much nastier example, choose a set of coset representatives for R/Q (or more generally R/S). Every element of R belongs to a unique coset of R/Q, so we can define a function R->R assigning a real number to the coset representative of the coset containing it. This function isn't even measurable.
Conceptually we can think of this construction as follows. If h:R->A is a homomorphism of abelian groups and A admits a function g satisfying the functional equation g(x+g(y))=g(y+g(x)) for all x,y, then any function s:A->R satisfying hs= id_A (i.e. any section, which we only require to be a function and not a homomorphism) induces a function f:R->R satisfying the functional equation. Specifically, f is given by f=sgh. Indeed, then
f(x+f(y))=sgh(x+sgh(y))=sg(h(x)+hsgh(y))=sg(h(x)+gh(y))=sg(h(y)+gh(x))=f (y+f(x)).
In our last example, h is the quotient map R->R/Q, g is the identity R/Q->R/Q, and s corresponds to the selection of a choice of coset representatives, where we have chosen the representative of Q to be 0.
For more down-to-earth examples, we could look at the homomorphism R->R/Z, with section given by the inclusion of R/Z into R as numbers x satisfying 0<=x<1. Again the identity R/Z->R/Z satisfies the functional equation, and the corresponding f:R->R is given by x->x (mod 1).
How much worse can these constructions get? Is f(x)=x+C the only nonconstant continuous solution?
It does follow from pex's argument that if f is continuously differentiable in a neighborhood of a point, then the derivative must be either 0 or 1. For if the derivative is nonzero, then f is locally injective and pex's argument applies to show that in fact the derivative is 1. Hence the only nonconstant globally continuously differentiable function f satisfying the equation is f(x)=x+C.
|
| « Last Edit: Sep 3rd, 2008, 5:06pm by Obob » |
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Functional equation
« Reply #7 on: Sep 4th, 2008, 1:00am » |
Quote Modify
|
on Sep 3rd, 2008, 3:21pm, Obob wrote:Consider the following function:
f(x)=x if x is irrational
f(x)=0 if x is rational.
Then
...
f(x+f(y))=y if x is rational and y is irrational
|
|
Hm...
if x is rational and y is irrational
f(x+f(y)) = f(x+y) = x+y
but
f(y+f(x)) = f(y+0) = y
so we don't have
f(x+f(y)) = f(y+f(x))
|
|
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: Functional equation
« Reply #8 on: Sep 4th, 2008, 1:22am » |
Quote Modify
|
My bad. You're right Grimbal.
The pathological example that I give later does work, however. In particular, the one where you pick coset representatives of R/Q.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print