 Author
Author |
Topic: Coin weighting using discrete math (Read 3057 times) |
|
wonderful
Full Member
  

Posts: 203
|
 |
Coin weighting using discrete math
« on: Aug 19th, 2008, 2:13pm » |
 Quote Quote  Modify Modify
|
There are two questions:
Q1. Given 6 idetical looking coins: A, B, C, D, E, F with corresponding weight: 1, 2, 3, 4, 5, 6.
Using a standard two-arm balance, can you design a weighting scheme to identify the weight of each of these six coins?
Q2. The same as above with 12 identical looking coins.
Have A Great Day!
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Coin weighting using discrete math
« Reply #1 on: Aug 20th, 2008, 6:25am » |
 Quote Quote  Modify Modify
|
Just any scheme, or the most efficient scheme? As an upper bound, 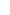 coins with known weights can be identified in coins with known weights can be identified in 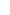  log2 log2 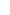  weighings by simply sorting them by weight. weighings by simply sorting them by weight.
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Coin weighting using discrete math
« Reply #2 on: Aug 20th, 2008, 7:38am » |
 Quote Quote  Modify Modify
|
It would be much easier to do it without weighing.
Just take a flat piece of board, put the coins on edge next to each other and tilt the board slightly. The fastest coin is lightest, the slowest heaviest etc.
(Although it assumes some measure of uniformity in the density of the coins)
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Coin weighting using discrete math
« Reply #3 on: Aug 20th, 2008, 8:12am » |
 Quote Quote  Modify Modify
|
You could use insertion into a balanced binary tree. It's pretty close to optimal; at least if you're limited to comparing two coins at a time (I'm not sure if comparing more at a time would give more information, but it's possible)
Optimal are 10 and 30; and I get 11 and 33
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
Modulo programming errors, question 1 can be solved in seven weightings.  (I haven't got to question 2 yet because MatLab won't let me store all the 12! permutations in one matrix.) (I haven't got to question 2 yet because MatLab won't let me store all the 12! permutations in one matrix.)
A theoretical lower bound is six, as each weighting has three possible outcomes and 35 < 6! < 36. Given the small slack (720 permutations versus 729 possible outcomes), I would be surprised if six were actually attainable.
Attached is the computer-generated weighting scheme. It's probably not the simplest possible, but it does seem to work.
|
|
 IP Logged IP Logged |
|
|
|
wonderful
Full Member
  

Posts: 203
|
 |
Re: Coin weighting using discrete math
« Reply #6 on: Aug 21st, 2008, 12:45pm » |
 Quote Quote  Modify Modify
|
Thanks guys for your excellent discussion. I am particularly impressed with Pex's solution which is very nicely done.
Have A Great Day!
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Coin weighting using discrete math
« Reply #7 on: Aug 21st, 2008, 3:34pm » |
 Quote Quote  Modify Modify
|
on Aug 20th, 2008, 1:33pm, pex wrote:Modulo programming errors, question 1 can be solved in seven weightings.  (I haven't got to question 2 yet because MatLab won't let me store all the 12! permutations in one matrix.) (I haven't got to question 2 yet because MatLab won't let me store all the 12! permutations in one matrix.)
A theoretical lower bound is six, as each weighting has three possible outcomes and 35 < 6! < 36. Given the small slack (720 permutations versus 729 possible outcomes), I would be surprised if six were actually attainable.
Attached is the computer-generated weighting scheme. It's probably not the simplest possible, but it does seem to work. |
|
Does an initial weighting exist such that the biggest part is  35=243? If not, the 7 weightings are surely optimal. 35=243? If not, the 7 weightings are surely optimal.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Coin weighting using discrete math
« Reply #8 on: Aug 21st, 2008, 10:35pm » |
 Quote Quote  Modify Modify
|
on Aug 21st, 2008, 3:34pm, Hippo wrote:
Does an initial weighting exist such that the biggest part is  35=243? If not, the 7 weightings are surely optimal. 35=243? If not, the 7 weightings are surely optimal. |
|
 should've thought of this myself... Of course, you're right. And no, such an initial weigting does not exist: my program works by picking a weighting such that the largest group left is as small as possible. For the initial weighting, that's 304. should've thought of this myself... Of course, you're right. And no, such an initial weigting does not exist: my program works by picking a weighting such that the largest group left is as small as possible. For the initial weighting, that's 304.
on Aug 21st, 2008, 12:45pm, wonderful wrote:Thanks guys for your excellent discussion. I am particularly impressed with Pex's solution which is very nicely done.
Have A Great Day! |
|
Thanks - but it's just brute-force programming; I didn't do much work...
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Coin weighting using discrete math
« Reply #9 on: Aug 22nd, 2008, 1:58am » |
 Quote Quote  Modify Modify
|
In the case of twelve coins the initial weighing gives a maximum information gain of about 0.886567 bits. You could use that approach recursively to find a probably optimal decision tree. But after the first weighing it takes a lot more computation to find out (because you lose all the symmetry of the initial position)
The best first move seems to be weighing 2 vs 3 balls. Which split the list of permutations into two groups of 224179200 and one of 30643200.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Coin weighting using discrete math
« Reply #10 on: Aug 22nd, 2008, 2:30am » |
 Quote Quote  Modify Modify
|
And it is possible that a sub-optimal first weighing leads to groups that can better be split in the second weighing. So it is not obvious that the optimal choice at each step, in terms of smallest size of the worst case, leads to a global optimum.
PS: oops, I just realized you said probably optimal. I agree with that.
|
| « Last Edit: Aug 22nd, 2008, 2:31am by Grimbal » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register