 Author
Author |
Topic: det of gcd (Read 1493 times) |
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
Find the determinant of the n x n matrix A defined by Ai,j = gcd(i,j).
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: det of gcd
« Reply #1 on: Jul 15th, 2008, 10:07am » |
 Quote Quote  Modify Modify
|
This problem looks very similar to me... I swear I saw it on this site, but cannot find it now...
I remeber the answer has something to do with totient function.

|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: det of gcd
« Reply #2 on: Jul 15th, 2008, 12:15pm » |
 Quote Quote  Modify Modify
|
It seems to be  in in  (i). (i).
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: det of gcd
« Reply #3 on: Jul 16th, 2008, 1:56pm » |
 Quote Quote  Modify Modify
|
Yes, that is correct. Do you have a proof?
I also thought this problem was here already, but I tried searching various combinations of det, determinant, gcd, hcf, matrix, phi, etc. Maybe it disappeared?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: det of gcd
« Reply #4 on: Jul 16th, 2008, 2:40pm » |
 Quote Quote  Modify Modify
|
How about:
Bi,j = i/gcd(i,j) = lcm(i,j)/j
Li,j = lcm(i,j)
Mi,j = i mod j, j>1; Mi,1=1.
What are some good binary number-theoretic functions?
(There are some other arithmetic matrix problems here, here, and here.)
|
| « Last Edit: Jul 16th, 2008, 10:01pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: det of gcd
« Reply #5 on: Jul 22nd, 2008, 1:28am » |
 Quote Quote  Modify Modify
|
on Jul 16th, 2008, 1:56pm, Eigenray wrote:| Yes, that is correct. Do you have a proof? |
|
After knowing the answer, several approaches are possible…
One of the proofs uses the Determinant Expansion by Minors (DEM). Although it’s not the easiest way to solve this problem, I would like to explore it here, since it gets at the answer from the basic matrix operations (the proof is based on Smith’s argument from back to 1876).
The idea is replace the n-th column of the matrix A(n) by linear combination of other columns in a way that all its elements but ann are equal to zero. Then, by the DEM, det(A(n)) = det(A(n-1)) ann.
Let p1, …, pm be distinct prime factors of n. As it is known, the totient function of n equals:
 (n) = n(1 – 1/p1)…(1 – 1/pm) (n) = n(1 – 1/p1)…(1 – 1/pm)
Now, if we open up the brackets in above formula, we will get a linear combination of 2m integers, half of them positive, and half negative (depending on the parity of pi’s in that term). Call the set of these integers the replacement vector. For example, when n = 6, the above formula gives 2 = 6 - 3 - 2 + 1, so the replacement vector is (1, -2, -3, 6).
Now, the replacement performed on the n-th column of matrix A(n) is as follows:
Replace the n-th column of A(n) by a signed sum of columns from replacement vector.
There is then a theorem stating that after such replacement, all elements of n-th column are equal to 0, except ann, which is just  (n). This actually gives the needed result. (n). This actually gives the needed result.
In case n = 6, matrix A(6) has the following entries:
| 1 1 1 1 1 1 |
| 1 2 1 2 1 2 |
| 1 1 3 1 1 3 |
| 1 2 1 4 1 2 |
| 1 1 1 1 5 1 |
| 1 2 3 2 1 6 |
Applying the above replacement, means adding columns 1 and 6, and subtracting columns 2 and 3, which gives a new vector (0 0 0 0 0 2), as required.
How do we prove the above theorem? Denote the replacement of the element akn by R(k,n). The following statements apply (the derivation is mine  ): ):
1. R(n, n) =  (n). (n).
2. R(1, n) = 0 for n > 1.
3. If q is a prime and R(k, n) = 0, then R(kq, nq) = 0.
4. If R(k, n) = 0 and gcd(q, n) = 1, then R(kq, n) = 0.
Long and boring? Maybe, but I liked to go through all the steps of the proof.
Much more elegant proofs exist. One is based on factoring the given matrix to a special matrix and its transpose.
|
| « Last Edit: Jul 22nd, 2008, 1:31am by Barukh » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: det of gcd
« Reply #6 on: Jul 22nd, 2008, 8:07am » |
 Quote Quote  Modify Modify
|
on Jul 22nd, 2008, 1:28am, Barukh wrote:
This is almost how I have computed the result  ... Actually I do it transposed ... Actually I do it transposed  . I have seen the resulting uptriangle matrix with . I have seen the resulting uptriangle matrix with  (n) on diagonal (after elimination). (n) on diagonal (after elimination).
|
| « Last Edit: Jul 22nd, 2008, 8:07am by Hippo » |
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: det of gcd
« Reply #7 on: Jul 22nd, 2008, 10:15am » |
 Quote Quote  Modify Modify
|
on Jul 22nd, 2008, 8:07am, Hippo wrote:
This is almost how I have computed the result  ... Actually I do it transposed ... Actually I do it transposed  . I have seen the resulting uptriangle matrix with . I have seen the resulting uptriangle matrix with  (n) on diagonal (after elimination). (n) on diagonal (after elimination). |
|
Nice work, Hippo!
on Jul 22nd, 2008, 1:28am, Barukh wrote:| Much more elegant proofs exist. One is based on factoring the given matrix to a special matrix and its transpose. |
|
The "civilized" proof goes like this (Beslin & Ligh, 89). Define an nxn matrix B = (bij) as follows: (B)ij =   (j), if j | i; 0, otherwise. B is a lower-triangular matrix with square roots of totient functions on the main diagonal. (j), if j | i; 0, otherwise. B is a lower-triangular matrix with square roots of totient functions on the main diagonal.
Then (BBT)ij =  kbikbjk = kbikbjk =  k|i, k|j k|i, k|j  (k) = (k) =  k|gcd(i,j) = gcd(i, j) = aij. k|gcd(i,j) = gcd(i, j) = aij.
Therefore, det(A) = det(B)det(BT) = det(B)2, as required.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: det of gcd
« Reply #8 on: Jul 22nd, 2008, 11:02am » |
 Quote Quote  Modify Modify
|
on Jul 22nd, 2008, 1:28am, Barukh wrote:| Now, if we open up the brackets in above formula, we will get a linear combination of 2m integers, half of them positive, and half negative (depending on the parity of pi’s in that term). Call the set of these integers the replacement vector. For example, when n = 6, the above formula gives 2 = 6 - 3 - 2 + 1, so the replacement vector is (1, -2, -3, 6). |
|
In other words, this replacement vector is { 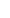 (d)*n/d }. So you're right-multiplying by the matrix Sij = (d)*n/d }. So you're right-multiplying by the matrix Sij = 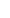 (j/i), if i | j. In fact, St A S is diagonal (j/i), if i | j. In fact, St A S is diagonal  This was the proof I had in mind. This was the proof I had in mind.
Quote:| Therefore, det(A) = det(B)det(BT) = det(B)2, as required. |
|
That is very nice! I was not aware of that one.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: det of gcd
« Reply #9 on: Jul 23rd, 2008, 12:45am » |
 Quote Quote  Modify Modify
|
on Jul 22nd, 2008, 11:02am, Eigenray wrote:
In other words, this replacement vector is { 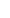 (d)*n/d }. (d)*n/d }. |
|
Yes, of course! Very nice. It makes the whole argument much more simple.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register