 Author
Author |
Topic: The Toad and the Water Lilies (Read 1328 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
The Toad and the Water Lilies
« on: Jun 6th, 2008, 9:40am » |
 Quote Quote  Modify Modify
|
A toad hops down a long line of water lilies. Before each hop it flips a fair coin to decide whether to hop two lilies forward or one lily back.
What is the expected fraction of the water lilies it will land on?
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: The Toad and the Water Lilies
« Reply #1 on: Jun 10th, 2008, 12:15pm » |
 Quote Quote  Modify Modify
|
Bit tricky, this one, but nice:
| hidden: | Let pn be the probability that the toad ever lands on the pad n units to the right.
We have p0 = 1, and for n != 0,
pn = (pn-2+pn+1)/2,
or pn+1 = 2pn - pn-2.
The characteristic polynomial of this recurrence is
x3 - 2x2 + 1 = (x-1)(x2-x-1),
which has roots 1, r, and s, where r = (1+sqrt 5)/2, s = (1-sqrt 5)/2.
But because the recurrence only holds for n!=0, we have to solve it twice:
pn = A + Brn + Csn, n >= -1;
pn = X + Yrn + Zsn, n <= 0.
This has 6 unknowns, but we also know the following:
(a) pn is bounded for all n. This gives B=0 and Z=0.
(b) pn converges to 0 as n goes to -infinity. This gives X=0.
(c) p0 = 1. This gives A+C=1, Y=1.
Equating the two formula for p-1 gives finally
1/r = A+C/s = A+(1-A)/s,
and therefore
A = (r-s)/[r(1-s)] = (3sqrt5 - 5)/2,
which is the limit of pn as n goes to infinity. |
We can also say that the expected value of the farthest left the toad ever goes is (1+sqrt5)/2.
|
| « Last Edit: Jun 10th, 2008, 12:17pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: The Toad and the Water Lilies
« Reply #2 on: Jun 12th, 2008, 6:14am » |
 Quote Quote  Modify Modify
|
Nicely done, Eigenray!  
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: The Toad and the Water Lilies
« Reply #3 on: Jun 12th, 2008, 7:23am » |
 Quote Quote  Modify Modify
|
on Jun 12th, 2008, 6:14am, Barukh wrote:Nicely done, Eigenray!   |
|
Yes, indeed!
A less classical, more hand-wavy sort of solution is as follows:
Let p = the probability that a toad starting at 1 regresses to 0 at some point.
To never regress it must jump forward (probability = 1/2) and not subsequently regress three times (probability = 1 - p3)
So we have
1 - p = (1 - p3)/2
giving
p = ( 5 - 1)/2 5 - 1)/2
Now consider the probability that during a particular jump the toad leaps over a lily that it never has and never will land on.
For this to happen it must
a) be jumping forward (probability = 1/2)
b) never regress from where it lands (probability = 1 - p)
c) not have reached in the past the lily it is jumping over (probability = 1 - p)
So the probability that a particular jump carries the toad over a skipped lily = (1 - p)2/2
Since the toad travels at an average rate of 1/2 lily per jump, the fraction of skipped lilies = (1 - p)2
Hence the fraction of water lilies it will land on
= 1 - (1 - p)2
= p(2 - p)
= (3 5 - 5)/2 5 - 5)/2 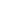 0.854102... 0.854102...
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
jollytall
Senior Riddler
   

Gender: 
Posts: 585
|
 |
Re: The Toad and the Water Lilies
« Reply #4 on: Aug 9th, 2008, 12:40pm » |
 Quote Quote  Modify Modify
|
Shouldn't it be devided by two, for he is only jumping - practically - into one direction? The question talks about a long line, not a half-line.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register