 Author
Author |
Topic: Rotating resistor wheel (Read 1301 times) |
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
A metal wheel, radius r, moment of inertia I, has n spokes, with n odd. Each spoke, and each arc between spokes, has a resistance R (imagine 2n resistors as shown in red). The wheel rotates through a fixed region of constant magnetic field B, which forms a sector with central angle 2 /n (shown in blue). /n (shown in blue).
Find the angular velocity  (t) in terms of its initial speed (t) in terms of its initial speed  0. 0.
(From a US Physics Team exam. n may have been given.)
|
|
 IP Logged IP Logged |

|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Rotating resistor wheel
« Reply #1 on: Jun 1st, 2008, 7:28pm » |
 Quote Quote  Modify Modify
|
Assuming B perpendicular torhe weel's plane, \omega = \omega_0 exp(-\lambda t) , where \lambda= B^2 r^4\divI(5+\sqrt5 +(2^n \sqrt5)/({3+\sqrt5}^{n-1}-2^{n-1}))R
Sorry: I tried Latex, as in the [ FAQ : how to write (and view) math symbols] , but seems it doesn't work ( so the preview...)
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Rotating resistor wheel
« Reply #2 on: Jun 2nd, 2008, 12:30am » |
 Quote Quote  Modify Modify
|
on Jun 1st, 2008, 7:28pm, Immanuel_Bonfils wrote:| Assuming B perpendicular torhe weel's plane, [hide]Sorry: I tried Latex, as in the [ FAQ : how to write (and view) math symbols] , but seems it doesn't work ( so the preview...) |
|
You need to have a plugin and a userscript installed for it to work (which is explained in the faq here).
It's not a full implementation of latex btw, it's only symbols, not other typographic functions. And the symbols aren't hidable either.
|
| « Last Edit: Jun 2nd, 2008, 12:31am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Rotating resistor wheel
« Reply #3 on: Jun 2nd, 2008, 2:59am » |
 Quote Quote  Modify Modify
|
Right, I forgot to say the field is perpendicular to the plane of the wheel.
on Jun 1st, 2008, 7:28pm, Immanuel_Bonfils wrote:| \omega = \omega_0 exp(-\lambda t) , where \lambda= B^2 r^4\divI(5+\sqrt5 +(2^n \sqrt5)/({3+\sqrt5}^{n-1}-2^{n-1}))R |
|
Yep! But I think the answer looks nicer if you don't express it in closed form. In fact, if you solve the problem in two different ways, you get a physical interpretation of a certain identity.
|
|
 IP Logged IP Logged |
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Rotating resistor wheel
« Reply #4 on: Jun 2nd, 2008, 9:37am » |
 Quote Quote  Modify Modify
|
Thanks towr but I had it already installed, and used  , for instance in an earlier post. The problem starts when I want powers or subscript like x^2 , x_0 in LaTex. Also I wonder if we can pull division like frac{x}{y} or {x , for instance in an earlier post. The problem starts when I want powers or subscript like x^2 , x_0 in LaTex. Also I wonder if we can pull division like frac{x}{y} or {x 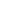 ver y} in tex... Could you, please, help me with that? ver y} in tex... Could you, please, help me with that?
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Rotating resistor wheel
« Reply #5 on: Jun 2nd, 2008, 10:16am » |
 Quote Quote  Modify Modify
|
on Jun 2nd, 2008, 9:37am, Immanuel_Bonfils wrote:Thanks towr but I had it already installed, and used  , for instance in an earlier post. The problem starts when I want powers or subscript like x^2 , x_0 in LaTex. , for instance in an earlier post. The problem starts when I want powers or subscript like x^2 , x_0 in LaTex. |
|
What the script does is replace codes for symbols with an image of the symbol; so anything else has to be done in another way.
To get a subscript or superscript, you can use [sub] or [sup] tags: x2 and x0
Quote:Also I wonder if we can pull division like frac{x}{y} or {x 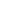 ver y} in tex... Could you, please, help me with that? ver y} in tex... Could you, please, help me with that? |
|
There really isn't a way to do that here, unfortunately. So you'd have to make do with the old fashioned x/y.
|
| « Last Edit: Jun 2nd, 2008, 10:29am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Rotating resistor wheel
« Reply #6 on: Jun 2nd, 2008, 10:28am » |
 Quote Quote  Modify Modify
|
on Jun 2nd, 2008, 9:37am, Immanuel_Bonfils wrote:| The problem starts when I want powers or subscript like x^2 , x_0 in LaTex. |
|
True, my script doesn't understand any markup/layout; it only makes a (fairly robust) set of symbols available under the same names they're known by in LaTeX. Superscripts can be done either through [sup], [/sup] tags (e.g. x[sup]2[/sup] gives x2), or most of the letter and number symbols have superscript equivalents (e.g. \x\sup2 gives   ). The same is true for subscripts. Be aware, though, that there is only one "level" of superscripts or subscripts available -- there's no clean way to handle x^y^z, for instance. ). The same is true for subscripts. Be aware, though, that there is only one "level" of superscripts or subscripts available -- there's no clean way to handle x^y^z, for instance.
Quote:| Also I wonder if we can pull division like frac{x}{y} or {x \over y} in tex... Could you, please, help me with that? |
|
Because we don't have much in the way of layout options, I think usually around here people just put the terms in parentheses if necessary and use a slash, e.g. x/y or (3x+2) / (y-5). I think once or twice I've been known to resort to a table with lines drawn from dashes, but that gets "messy" very quickly.
Sorry we can't offer better formula capability at the moment, but it's still better than *most* furums where you're limited to text alone...
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Rotating resistor wheel
« Reply #7 on: Jun 2nd, 2008, 10:38am » |
 Quote Quote  Modify Modify
|
Thanks People, you're quite cool!
|
|
 IP Logged IP Logged |
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Rotating resistor wheel
« Reply #8 on: Jun 3rd, 2008, 11:10am » |
 Quote Quote  Modify Modify
|
Eigenray
I'm not sure I've got your idea. Could you be more explicit?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Rotating resistor wheel
« Reply #9 on: Jun 3rd, 2008, 12:08pm » |
 Quote Quote  Modify Modify
|
Well, how did you solve it?
By the way, the case of n even is not really any harder, but the associated sequence is less well known.
|
|
 IP Logged IP Logged |
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Rotating resistor wheel
« Reply #10 on: Jun 3rd, 2008, 3:40pm » |
 Quote Quote  Modify Modify
|
OK
The electromotive force is  = B = B 0r {v dx}, where x localizes the generic spoke’s point P, relative the center, and v= 0r {v dx}, where x localizes the generic spoke’s point P, relative the center, and v= x is its velocity. So x is its velocity. So  =0.5 B =0.5 B .r2. We could get it, also from Faraday’s Law. .r2. We could get it, also from Faraday’s Law.
This “source” induces the current in the whole rod but the arc opposite the spoke considered above, ( that , by the way, is the only one immersed in the magnetic field in each moment), cause, by symmetry the current gets null and we can open the circuit there.
Now it's a matter of equivalent resistance in each half of the rod , associating R in series , parallel, series, parallel…(n-1)/2 times, and this leads to quotient of Fibonacci numbers (the source has an internal resistance R itself).
Getting the current , i = ( B r2/(kR), where k, dependent of n, comes from the circuit analysis, we can calculate the elementary force of the field on the point P and its corresponding torque and integrate to get B r2/(kR), where k, dependent of n, comes from the circuit analysis, we can calculate the elementary force of the field on the point P and its corresponding torque and integrate to get 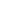 = ( = ( B2 r4)/(2kR). B2 r4)/(2kR).
The movement equation 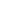 = - I (d = - I (d )/(dt), leads to the answer hidden in my first post, above. )/(dt), leads to the answer hidden in my first post, above.
I will think about the even case
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Rotating resistor wheel
« Reply #11 on: Jun 4th, 2008, 5:55am » |
 Quote Quote  Modify Modify
|
I did it slightly differently, using symmetry and Faraday (and Kirchoff) to find the current through each resistor.
on Jun 3rd, 2008, 3:40pm, Immanuel_Bonfils wrote:| this leads to quotient of Fibonacci numbers |
|
Yes that was what I was getting at. We can express it as
 = - = - * B2r4/(2RI) * Fn-1/(Fn-1+Fn+1), * B2r4/(2RI) * Fn-1/(Fn-1+Fn+1),
which is prettier.
Now, what do you get if you add up all the power losses over each resistor in the circuit?
|
|
 IP Logged IP Logged |
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Rotating resistor wheel
« Reply #12 on: Jun 4th, 2008, 6:55am » |
 Quote Quote  Modify Modify
|
I see. By closed form you mean substituting Fibonacci numbers by their "numerical" expression? ( one could say this is a open form...).
And is always a good advise to make an "enrgetic check"(he he he), but seams we can't solve it this way... unfortunately.
// Excessive whitespace removed by Eigenray
|
| « Last Edit: Jun 4th, 2008, 7:50am by Eigenray » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Rotating resistor wheel
« Reply #13 on: Jun 4th, 2008, 7:46am » |
 Quote Quote  Modify Modify
|
I just mean that expressing it in terms of the Fibonacci numbers is more illuminating. We can always plug in the closed form for them, but it hides what's going on.
The currents through the resistors are
F1x, F2x, ..., and Fn-1x, each occuring twice; and 0 and 2Fn-1x, where
x = Br2 /[2R(Fn-1+Fn+1)]. /[2R(Fn-1+Fn+1)].
If we add up all the power losses,
P = [ 2(F12 + ... + Fn-12) + 4Fn-12 ] * x2 R,
we find that
P = B2r4 2/(2R) * Fn-1/(Fn-1+Fn+1) 2/(2R) * Fn-1/(Fn-1+Fn+1)
= - d/dt [ I 2/2 ]. 2/2 ].
Why is this?
|
|
 IP Logged IP Logged |
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Rotating resistor wheel
« Reply #14 on: Jun 4th, 2008, 11:41am » |
 Quote Quote  Modify Modify
|
Tested!
Thanks for fixing that excessive white space (rather black...). By the way, how can I use the Search tab? I just tried " Rotating resistor wheel" and it gives back "Sorry, no matches where found" !
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Rotating resistor wheel
« Reply #15 on: Jun 4th, 2008, 12:06pm » |
 Quote Quote  Modify Modify
|
It works for me. You did remember to check the box for the medium forum, right? (I still forget to check them myself sometimes.)
And you can edit your own posts, by the way, using the 'Modify' link in the upper right of each post.
|
| « Last Edit: Jun 4th, 2008, 12:08pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Immanuel_Bonfils
Junior Member
 

Posts: 114
|
 |
Re: Rotating resistor wheel
« Reply #16 on: Jun 10th, 2008, 3:41pm » |
 Quote Quote  Modify Modify
|
I forgot about the even n.
A conversion of wye to delta in the node opposite to the “active” spoke, introduces three 3R resistor , but the “delta’s base” can be removed, since by symmetry the current is null. Like the odd case, successive series and parallel association leads to the Lucas Numbers, L[sub] j [\sub] instead of Fobnacci’s.
|
| « Last Edit: Jun 10th, 2008, 3:44pm by Immanuel_Bonfils » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register