 Author
Author |
Topic: prove that (Read 797 times) |
|
tony123
Junior Member
 

Posts: 61
|
cos(pi/14)cos(3pi/14)cos(5pi/14)=sqrt7/8
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: prove that
« Reply #1 on: Mar 5th, 2008, 7:26pm » |
 Quote Quote  Modify Modify
|
A little clarification:
cos( /14) cos(3 /14) cos(3 /14) cos(5 /14) cos(5 /14) = 71/2 / 8. /14) = 71/2 / 8.
By "an amazing coincidence",
cos( /14) + cos(3 /14) + cos(3 /14) - cos(5 /14) - cos(5 /14) = 71/2 / 2. /14) = 71/2 / 2.
|
| « Last Edit: Mar 5th, 2008, 7:29pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: prove that
« Reply #2 on: Mar 6th, 2008, 1:20pm » |
 Quote Quote  Modify Modify
|
I think complex numbers will handle this pretty easily. I have tried to avoid using complex numbers... but the ideas are similar I guess
Notice that the product is positive. Now square it
and use cos2x = (cos2x+1)/2
We now are looking for
(1+ cos pi/7) (1 + cos 3pi/7) (1 + cos 5pi/7)/8
For x = pi/7, 3pi/7, 5pi/7 and 7pi/7
notice that they all satisfy
cos 3x + cos 4x = 0
Treating this as a polynomial in y = cosx we get:
P(y) = (-3y + 4y3 + 1 - 8y2 + 8y4 )/8 = 0
(we divide by 8 to get a monic polynomial)
This is a 4th degree polynomial whose only roots are cos x for x = pi/7, 3pi/7, 5pi/7 and 7pi/7
i.e P(y) = (y+1)(y - cos pi/7)(y- cos 3pi/7)(y - 5pi/7)
Let H(y) = (y - cos pi/7)(y- cos 3pi/7)(y - 5pi/7)
i.e. P(y) = (y+1) H(y)
Now differentiate wrt y
P'(y) = H'(y)(y+1) + H(y) ---- ( 1 )
We are interested in finding -H(-1)/8.
Put y = -1 in ( 1 ) we see that
-H(-1) = -P'(-1)
Now -P'(y) = (32y3 + 12y2 - 16y - 3)/8
So -P'(-1) = (32 - 12 - 16 + 3)/8 = 7/8
Thus -H(-1)/8 = 7/64.
Thus the required answer is sqrt(7/64) = sqrt(7)/8
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: prove that
« Reply #3 on: Mar 6th, 2008, 3:30pm » |
 Quote Quote  Modify Modify
|
We have more generally that
p =  k=1n cos[ k=1n cos[ (2k-1)/(4n+2)] = (2k-1)/(4n+2)] =  [2n+1]/2n, [2n+1]/2n,
since if we write cos[(2n+1)z]/cos[z] = F(cos z), where F is a polynomial of degree 2n, then the product of the roots of F is (-1)n p2.
On the other hand,
 k=1n sin[ k=1n sin[ (2k-1)/(4n+2)] = 1/2n, (2k-1)/(4n+2)] = 1/2n,
 k=1n cos[ k=1n cos[ (2k-1)/(4n)] = (2k-1)/(4n)] =  k=1n sin[ k=1n sin[ (2k-1)/(4n)] = (2k-1)/(4n)] =  2/2n 2/2n
are not quite as interesting.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: prove that
« Reply #4 on: Mar 6th, 2008, 3:36pm » |
 Quote Quote  Modify Modify
|
Let m=2n+1. The first equality shows that  ( ( m) is contained in the totally real subfield m) is contained in the totally real subfield  (cos[2 (cos[2 /(4m)]) = /(4m)]) =  ( ( +1/ +1/ ) = ) =  ( ( ) )  of of  ( ( ), where ), where  = = 4m is a primitive 4m-th root of unity. We have Gal( 4m is a primitive 4m-th root of unity. We have Gal( ( ( )/ )/ ) ~= (Z/(4m))*, and Gal( ) ~= (Z/(4m))*, and Gal( ( ( )/ )/ ( ( +1/ +1/ )) ~= { )) ~= { 1} under the same isomorphism. So Gal( 1} under the same isomorphism. So Gal( ( ( +1/ +1/ )/ )/ ) ~= (Z/(4m))*/{ ) ~= (Z/(4m))*/{ 1} ~= (Z/m)*. So 1} ~= (Z/m)*. So  ( ( +1/ +1/ ) contains 2r-1 (real) quadratic subfields, where r is the number of distinct prime factors of m. For example, we can express ) contains 2r-1 (real) quadratic subfields, where r is the number of distinct prime factors of m. For example, we can express  3, 3,  5, and 5, and  15 as polynomials in cos( 15 as polynomials in cos( /30). [If p is an (odd) prime factor of m, then /30). [If p is an (odd) prime factor of m, then  p p   (cos[2 (cos[2 /(4p)]) = /(4p)]) =  ( ( 4p) 4p)  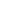  ( ( 4m) 4m)  = =  (cos[2 (cos[2 /(4m)]).] /(4m)]).]
Now, Gal( ( ( 4)/ 4)/ ) ~ (Z/m)* as well, so ) ~ (Z/m)* as well, so  ( ( 4) has the same number of quadratic subfields (and, moreover, an isomorphic lattice of subfields) as 4) has the same number of quadratic subfields (and, moreover, an isomorphic lattice of subfields) as  ( ( +1/ +1/ ), but they won't all be real; e.g., we can express ), but they won't all be real; e.g., we can express  {-3}, {-3},  5, and 5, and  {-15} as polynomials in {-15} as polynomials in  4 = e2 4 = e2 i/15, but not i/15, but not  3, say. 3, say.
And finally, Gal( ( ( )/ )/ ) ~= (Z/(4m))* ~= (Z/4)* x (Z/m)*, so we can find 2r+1 - 1 quadratic subfields of ) ~= (Z/(4m))* ~= (Z/4)* x (Z/m)*, so we can find 2r+1 - 1 quadratic subfields of  ( ( ); e.g., we can express any product of i= ); e.g., we can express any product of i= {-1}, {-1},  3, and 3, and  5 as polynomials in 5 as polynomials in  =e2 =e2 i/60. i/60.
|
|
 IP Logged IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: prove that
« Reply #5 on: Mar 8th, 2008, 3:53am » |
 Quote Quote  Modify Modify
|
Your posts always have me running to my textbooks Eigenray! (That is a good thing  ). ).
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: prove that
« Reply #6 on: Mar 8th, 2008, 10:49am » |
 Quote Quote  Modify Modify
|
Aryabhatta: I have absolutely the same feeling unfortunately it seems to me I will end uneducated 
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: prove that
« Reply #7 on: Mar 8th, 2008, 10:18pm » |
 Quote Quote  Modify Modify
|
To go into a bit more detail:
Fix an odd integer n. A question we might ask is: for which d can we express  d as a polynomial in either d as a polynomial in either  n = e2 n = e2 i/n, an n-th root of unity, or maybe C4n = cos(2 i/n, an n-th root of unity, or maybe C4n = cos(2 /4n) = ( /4n) = ( 4n+1/ 4n+1/ 4n)/2. 4n)/2.
The current problem generalizes to show that for any d | n, we can express  d as a polynomial in C4n. Thus, d as a polynomial in C4n. Thus,  ( ( d) d) 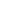  (C4n). Another argument shows that if p | n is prime, then (C4n). Another argument shows that if p | n is prime, then  {p*} {p*}   ( ( n), where p* = (-1)(p-1)/2p n), where p* = (-1)(p-1)/2p  1 mod 4. This gives at least 2r-1 distinct quadratic subfields, where r is the number of prime factors of n, in either case. 1 mod 4. This gives at least 2r-1 distinct quadratic subfields, where r is the number of prime factors of n, in either case.
On the other hand, we can show that these are the only such d, i.e.,  (C4n) and (C4n) and  ( ( n) both posses only 2r-1 quadratic subfields. n) both posses only 2r-1 quadratic subfields.
To do this consider for a moment an arbitrary field extension L/K, and let G=Aut(L/K) be the group of automorphisms of L that fix K. Given an intermediate field E, with K 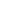 E E 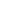 L, we can form Aut(L/E), a subgroup of G. Conversely, given a subgroup H of G, we can form LH, the subfield of L consisting of those elements fixed by every element of H. Clearly E L, we can form Aut(L/E), a subgroup of G. Conversely, given a subgroup H of G, we can form LH, the subfield of L consisting of those elements fixed by every element of H. Clearly E 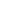 LAut(L/E), and H LAut(L/E), and H  Aut(L/LH). Aut(L/LH).
It turns out that in that case K= , if L is obtained by adjoining to , if L is obtained by adjoining to  all the roots of a polynomial with rational coefficients, then L/K is what's called a Galois extension: the operations E all the roots of a polynomial with rational coefficients, then L/K is what's called a Galois extension: the operations E 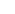 Aut(L/E) and H Aut(L/E) and H 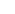 LH are inverses to each other, and give a bijection between the set of subfields of L containing K, and the set of subgroups of G=Aut(L/K). Moreover, this is an inclusion reversing lattice isomorphism, and one of its properties is that if H=Aut(L/E), or equivalently, E=LH, then [E:K] = [G:H]. So there is a bijection between subfields of L, quadratic over K, and subgroups of G of index 2. LH are inverses to each other, and give a bijection between the set of subfields of L containing K, and the set of subgroups of G=Aut(L/K). Moreover, this is an inclusion reversing lattice isomorphism, and one of its properties is that if H=Aut(L/E), or equivalently, E=LH, then [E:K] = [G:H]. So there is a bijection between subfields of L, quadratic over K, and subgroups of G of index 2.
In our case, let m be arbitrary. Then L= ( ( m) is Galois over m) is Galois over  , since it's the splitting field of the polynomial zm-1. Therefore there is a bijection between the subfields of L, and the subgroups of Aut(L/ , since it's the splitting field of the polynomial zm-1. Therefore there is a bijection between the subfields of L, and the subgroups of Aut(L/ ). Any automorphism over L over ). Any automorphism over L over  is determined by what it does to is determined by what it does to  ; since it must take ; since it must take  to to  a for some a relatively prime to m, there are no more than a for some a relatively prime to m, there are no more than  (m) automorphisms. On the other hand, one has [L: (m) automorphisms. On the other hand, one has [L: ] = ] =  (m), the degree of the m-th cyclotomic polynomial, so by Galois theory, |Aut(L/ (m), the degree of the m-th cyclotomic polynomial, so by Galois theory, |Aut(L/ )| = [L: )| = [L: ] = ] =  (m), and therefore Aut(L/ (m), and therefore Aut(L/ ) = ( ) = ( /m)*. /m)*.
|
| « Last Edit: Mar 8th, 2008, 10:36pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: prove that
« Reply #8 on: Mar 8th, 2008, 10:18pm » |
 Quote Quote  Modify Modify
|
Another property of the Galois connection is that if N = Aut(L/E)  G is a normal subgroup, then E is Galois over K, with Galois group G/N; i.e., Aut(L/K)/Aut(L/E) = Aut(E/K). In our case, since G is abelian, every subgroup is normal, so every intermediate field is also Galois over G is a normal subgroup, then E is Galois over K, with Galois group G/N; i.e., Aut(L/K)/Aut(L/E) = Aut(E/K). In our case, since G is abelian, every subgroup is normal, so every intermediate field is also Galois over  . .
Take E =  (Cm) = (Cm) =  ( ( +1/ +1/ ). Since ). Since  satisfies satisfies  2 - ( 2 - ( +1/ +1/ ) ) + 1 = + 1 =  2 - 2C 2 - 2C + 1 = 0, + 1 = 0,  has degree no more than 2 over E. On the other hand, E has degree no more than 2 over E. On the other hand, E 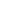  , so , so  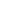 E. Therefore [L:E]=2, and E = L E. Therefore [L:E]=2, and E = L  . Note that complex conjugation is an automorphism of L over E; since |Aut(L/E)| = [L:E] = 2, this is the only non-trivial element of Aut(L/E). Since complex conjugation takes . Note that complex conjugation is an automorphism of L over E; since |Aut(L/E)| = [L:E] = 2, this is the only non-trivial element of Aut(L/E). Since complex conjugation takes  to to  -1, Aut(L/E) = { -1, Aut(L/E) = { 1}, when we identify Aut(L/ 1}, when we identify Aut(L/ ) = ( ) = ( /m)*. /m)*.
So Aut(E/ ) = Aut(L/ ) = Aut(L/ )/Aut(L/E) = ( )/Aut(L/E) = ( /m)*/{ /m)*/{ 1}. Now suppose m=4n, where n is odd. Then ( 1}. Now suppose m=4n, where n is odd. Then ( /m)* ~= ( /m)* ~= ( /4)* x ( /4)* x ( /n)* by the Chinese remainder theorem, where the isomorphism is (a mod 4n) /n)* by the Chinese remainder theorem, where the isomorphism is (a mod 4n) 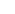 (a mod 4, a mod n). Note that (-1) (a mod 4, a mod n). Note that (-1) 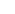 (-1,-1). Define (-1,-1). Define  : ( : ( /4)* x ( /4)* x ( /n)* /n)*  ( ( /n)* by /n)* by  ( ( 1,x) = ( 1,x) = ( x). This is clearly a surjective homomorphism with kernel <(-1,-1)>. By the first isomorphism theorem, x). This is clearly a surjective homomorphism with kernel <(-1,-1)>. By the first isomorphism theorem,
Aut(E/ ) = ( ) = ( /4n)*/{ /4n)*/{ 1} = (( 1} = (( /4)* x ( /4)* x ( /n)*)/<(-1,-1)> ~= ( /n)*)/<(-1,-1)> ~= ( /n)*. /n)*.
Now by Galois theory, the quadratic subfields of E correspond to the subgroups of Aut(E/ ) of index 2. But any finite abelian group is self-dual: the subgroups of index 2 correspond (non-canonically) to the subgroups of order 2. By the Chinese remainder theorem, if n = ) of index 2. But any finite abelian group is self-dual: the subgroups of index 2 correspond (non-canonically) to the subgroups of order 2. By the Chinese remainder theorem, if n =  pk, then ( pk, then ( /n)* ~= /n)* ~=  ( ( /pk)*. So the elements of order 2 correspond to picking an element of order 1 or 2 in each factor, but not all 1. Since each factor is cyclic of even order pk-1(p-1), the number of elements of order 2 is exactly 2r-1. /pk)*. So the elements of order 2 correspond to picking an element of order 1 or 2 in each factor, but not all 1. Since each factor is cyclic of even order pk-1(p-1), the number of elements of order 2 is exactly 2r-1.
The same is true for  ( ( n), since Aut( n), since Aut( ( ( n)/ n)/ ) = ( ) = ( /n)* as well. In this case the quadratic subfields are given by /n)* as well. In this case the quadratic subfields are given by  ( ( d*), where d | n, and d* = d*), where d | n, and d* =  d d  1 mod 4, whereas the quadratic subfields of 1 mod 4, whereas the quadratic subfields of  (cos(2 (cos(2 /4n)) are given simply by /4n)) are given simply by  ( ( d), with d|n. d), with d|n.
|
| « Last Edit: Mar 8th, 2008, 10:36pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: prove that
« Reply #9 on: Mar 8th, 2008, 10:19pm » |
 Quote Quote  Modify Modify
|
With a bit more work one can consider the case  ( ( m) for m even, too. The general case m) for m even, too. The general case  (cos(2 (cos(2 /m)) is trickier: what is ( /m)) is trickier: what is ( /m)*/<-1>? /m)*/<-1>?
But we don't actually need to determine the group. An element of order 1 or 2 in the quotient corresponds to an element of order 1,2, or 4 in ( /m)*. Write m = 2an, where n is odd, with r distinct prime factors. The number of elements of order 1 or 2 is 2r, if a<2; 2r+1 if a=2; and 2r+2 if a>2. The number of elements of order 4 is 0 if -1 is not a square mod m, and 2r otherwise. But in the quotient, we only have half as many elements (for m>2). So the number of quadratic subfields of /m)*. Write m = 2an, where n is odd, with r distinct prime factors. The number of elements of order 1 or 2 is 2r, if a<2; 2r+1 if a=2; and 2r+2 if a>2. The number of elements of order 4 is 0 if -1 is not a square mod m, and 2r otherwise. But in the quotient, we only have half as many elements (for m>2). So the number of quadratic subfields of  (cos(2 (cos(2 /m)) is the number of elements of ( /m)) is the number of elements of ( /m)*/<-1> of order 2, which is: /m)*/<-1> of order 2, which is:
a=0,1: 2r-1-1 if (-1|n)=-1, 2r-1 if (-1|n)=1.
a=2: 2r-1
a>2: 2r+1-1.
If n is odd, then  ( ( n)= n)= ( ( 2n), so their intersections with 2n), so their intersections with  are equal as well. So the result is the same for a=0 as a=1. are equal as well. So the result is the same for a=0 as a=1.
Let p1,...,ps,q1,...,qt be the primes dividing n, with pi=1 mod 4, qj=3 mod 4. Then the quadratic subfields of  ( ( n) or n) or  ( ( 2n) are 'generated' by 2n) are 'generated' by  pi and pi and  {-qj}, for a total of 2s+t-1. The quadratic subfields of {-qj}, for a total of 2s+t-1. The quadratic subfields of  (cos(2 (cos(2 /n)) or /n)) or  (cos(2 (cos(2 /2n)) are exactly those of /2n)) are exactly those of  ( ( n) which are real, and these are 'generated' by n) which are real, and these are 'generated' by  pi, and pi, and  {q1qj}, 1<j {q1qj}, 1<j t, and there are 2s+max(t-1,0)-1 of these. If t=0, then (-1|n)=1, and this is 2r-1. If t>0, then (-1|n)=-1, and this is 2r-1-1. t, and there are 2s+max(t-1,0)-1 of these. If t=0, then (-1|n)=1, and this is 2r-1. If t>0, then (-1|n)=-1, and this is 2r-1-1.
If a=2, i.e., m=4n, then the quadratic subfields of  ( ( m) are generated by I, m) are generated by I,  pi, and pi, and  {-qj}, for a total of 2r+1-1. Since {-qj}, for a total of 2r+1-1. Since  {-1} {-1}  ( ( 4n), the real ones are generated by 4n), the real ones are generated by  pi, pi,  qj, for a total of 2r-1. qj, for a total of 2r-1.
Finally, if a>2, i.e., 8|m, then we also get  2 in both 2 in both  ( ( m) and m) and  (cos(2 (cos(2 /m)), so the number of quadratic subfields are 2r+2-1 and 2r+1-1, respectively. /m)), so the number of quadratic subfields are 2r+2-1 and 2r+1-1, respectively.
For example:
m=2: cos(2 /2)=-1, degree 1. a=1,n=1,r=0, #QS = 20-1=0. /2)=-1, degree 1. a=1,n=1,r=0, #QS = 20-1=0.
m=3: cos(2 i/3)=-1/2, degree 1. a=0,n=3, r=1, (-1|n)=-1, #QS = 21-1-1=0. i/3)=-1/2, degree 1. a=0,n=3, r=1, (-1|n)=-1, #QS = 21-1-1=0.
m=4: cos(2 i/4)=0, degree 1. a=2,n=1, r=0, #QS = 20-1. i/4)=0, degree 1. a=2,n=1, r=0, #QS = 20-1.
m=5: cos(2 i/5)=( i/5)=( 5-1)/4, degree 2. a=0,n=5, r=1, (-1|n)=1, #QS = 21-1=1. 5-1)/4, degree 2. a=0,n=5, r=1, (-1|n)=1, #QS = 21-1=1.
m=6: cos(2 i/6)=1/2, degree 1. m=2*3, same field as m=3. i/6)=1/2, degree 1. m=2*3, same field as m=3.
m=7: cos(2 i/7) has degree 3. a=0,n=7, r=1, (-1|n)=-1, #QS = 21-1-1=0. i/7) has degree 3. a=0,n=7, r=1, (-1|n)=-1, #QS = 21-1-1=0.
m=8: cos(2 i/8)=1/ i/8)=1/ 2. a=3,n=1,r=0. #QS = 20+1-1 = 1. 2. a=3,n=1,r=0. #QS = 20+1-1 = 1.
m=9: cos(2 i/9), degree 3. a=0,n=9, r=1, (-1|n)=-1, #QS = 21-1-1 = 0. i/9), degree 3. a=0,n=9, r=1, (-1|n)=-1, #QS = 21-1-1 = 0.
m=10: cos(2 i/10)=( i/10)=( 5+1)/4, degree 2, same field as m=5. 5+1)/4, degree 2, same field as m=5.
m=12: cos(2 i/12)= i/12)= 3/2, degree 2, a=2,n=3, r=1, #QS=21-1=1. 3/2, degree 2, a=2,n=3, r=1, #QS=21-1=1.
|
| « Last Edit: Mar 8th, 2008, 10:29pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register