 Author
Author |
Topic: Triangles and quadrilaterals with given perimeter (Read 4126 times) |
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Triangles and quadrilaterals with given perimeter
« on: Feb 6th, 2008, 10:53am » |
 Quote Quote  Modify Modify
|
I found simple proofs of:
Among all triangles with a given perimeter, the equilateral triangle has the largest area.
Among all quadrilaterals in the plane, the square has the largest area.
But I was told that this is a "classic" resut. Does anyone know this result? Does it hold for planar n-gons with n>4?
|
|
 IP Logged IP Logged |
|
|
|
JohanC
Senior Riddler
   

Posts: 460
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #1 on: Feb 6th, 2008, 1:01pm » |
 Quote Quote  Modify Modify
|
I don't have an answer to your questions, but you might be interested in Thomas Hales' 2001 paper about the Honeycomb Conjecture. It gives the impression that it's not too obvious.
|
|
 IP Logged IP Logged |
|
|
|
Random Lack of Squiggily Lines
Senior Riddler
   

Everything before 7/1/2008 is now irrelevant.
Gender: 
Posts: 460
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #3 on: Feb 7th, 2008, 4:08am » |
 Quote Quote  Modify Modify
|
well, since the circle has largest area of all shapes, the equilateral triangle and normal square are closest to the shape
|
|
 IP Logged IP Logged |
You can only believe i what you can prove, and since you have nothing proven to cmpare to, you can believe in nothing.
I have ~50 posts to hack a "R" into a "D". Which one?
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #4 on: Feb 7th, 2008, 9:29am » |
 Quote Quote  Modify Modify
|
Thanks for the link, Sir Col. Simple proofs, indeed, for triangles and quadrilaterals. However, none of the proofs there show that a pentagon with given perimeter and maximum area must be regular. Both proofs show that all sides have the same length but assume that the vertices lie on a circle.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: Triangles and quadrilaterals with given perime 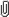 Quadr.PNG Quadr.PNG
« Reply #5 on: Feb 7th, 2008, 10:13am » |
 Quote Quote  Modify Modify
|
on Feb 7th, 2008, 9:29am, ecoist wrote:| Thanks for the link, Sir Col. Simple proofs, indeed, for triangles and quadrilaterals. However, none of the proofs there show that a pentagon with given perimeter and maximum area must be regular. Both proofs show that all sides have the same length but assume that the vertices lie on a circle. |
|
"Dr. Rob" only requires knowledge of the fact that for given (not necessarily equal) side lengths, the quadrilateral of largest area is cyclic. This is not hard to show.
See the attached picture. The are of the quadrilateral is (ab sin + cd sin + cd sin )/2. Further, using the cosine rule to express the length of the diagonal in two ways, a2+b2-2ab cos )/2. Further, using the cosine rule to express the length of the diagonal in two ways, a2+b2-2ab cos = c2+d2-2cd cos = c2+d2-2cd cos . .
Using the standard Lagrangian technique for constrained optimization with respect to  and and  , maximal area is obtained in a situation satisfying , maximal area is obtained in a situation satisfying
(1/2)ab cos + 2 + 2 ab sin ab sin = 0; = 0;
(1/2)cd cos - 2 - 2 cd sin cd sin = 0. = 0.
Eliminating the Lagrangian multiplier  , cos , cos /sin /sin = - cos = - cos /sin /sin , or tan , or tan = - tan = - tan . The only way this can be satisfied with 0 < . The only way this can be satisfied with 0 <  + +  < 2 < 2 is if is if  + +  = =  ; that is, the quadrilateral is cyclic. ; that is, the quadrilateral is cyclic.
|
| « Last Edit: Feb 7th, 2008, 10:13am by pex » |
 IP Logged IP Logged |

|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #6 on: Feb 7th, 2008, 10:58am » |
 Quote Quote  Modify Modify
|
Gosh, pex! My proof for the quadrilateral does not require that "the quadrilateral of largest area is cyclic"!
Let ABCD be a quadrilateral in the plane labelled clockwise, with maximum area among quadrilaterals with the same perimeter. Select diagonal AC. Then B lies on an ellipse with foci A and C. Hence, if AB=/=BC, then we can move B along the ellipse, preserving AB+BC, until AB=BC, where the area of triangle ABC is larger. Thus, all sides of ABCD must equal. Hence ABCD is a rhombus. Since the area is maximum, this rhombus must be a square.
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #7 on: Feb 7th, 2008, 11:27am » |
 Quote Quote  Modify Modify
|
on Feb 7th, 2008, 10:58am, ecoist wrote:| Since the area is maximum, this rhombus must be a square. |
|
That's not obvious unless you allow the result that you claim not to require, or show it some other way...
|
|
 IP Logged IP Logged |
|
|
|
Sir Col
Uberpuzzler
    

impudens simia et macrologus profundus fabulae

Gender: 
Posts: 1825
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #8 on: Feb 7th, 2008, 11:37am » |
 Quote Quote  Modify Modify
|
on Feb 7th, 2008, 9:29am, ecoist wrote:| Thanks for the link, Sir Col. Simple proofs, indeed, for triangles and quadrilaterals. However, none of the proofs there show that a pentagon with given perimeter and maximum area must be regular. Both proofs show that all sides have the same length but assume that the vertices lie on a circle. |
|
Not quite, "Dr. Rob" shows that an n-gon of fixed perimeter has maximum area when it is a regular. He does this in three steps:
(1) Show that the polygon must be convex.
(2) Show that the polygon must equilateral.
(3) Show that the polygon must be equiangular.
|
|
 IP Logged IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #9 on: Feb 7th, 2008, 11:40am » |
 Quote Quote  Modify Modify
|
Why isn't it obvious, rmsgrey? The area of a rhombus is the length of a side times the distance between opposite sides. If the rhombus is not a square, then the distance between opposite sides is less than a side length.
|
|
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #10 on: Feb 7th, 2008, 11:54am » |
 Quote Quote  Modify Modify
|
Sorry, Sir Col, I couldn't find any argument there even remotely related to (3).
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #11 on: Feb 7th, 2008, 12:25pm » |
 Quote Quote  Modify Modify
|
on Feb 7th, 2008, 11:40am, ecoist wrote:| Why isn't it obvious, rmsgrey? The area of a rhombus is the length of a side times the distance between opposite sides. If the rhombus is not a square, then the distance between opposite sides is less than a side length. |
|
It's not so obvious when you're more used to calculating the area of a rhombus by treating it as a kite rather than a parallelogram...
|
|
 IP Logged IP Logged |
|
|
|
Sir Col
Uberpuzzler
    

impudens simia et macrologus profundus fabulae

Gender: 
Posts: 1825
|
 |
Re: Triangles and quadrilaterals with given perime
« Reply #12 on: Feb 7th, 2008, 1:02pm » |
 Quote Quote  Modify Modify
|
on Feb 7th, 2008, 11:54am, ecoist wrote:| Sorry, Sir Col, I couldn't find any argument there even remotely related to (3). |
|
Here is "Dr. Rob's" non-calculus approach...
Step 1: Show that a polygon with a fixed perimeter and largest area must be convex. Do this by considering any vertex with an interior angle of more than 180 degrees, and constructing the diagonal connecting the two vertices adjacent. The diagonal and the two edges will form a triangle. Reflect that triangle in the line that is the diagonal extended, and you have a polygon with a larger area and the same perimeter.
Step 2: Show that a convex polygon with a fixed perimeter and largest area must have all sides of the same length. Do this by looking at two unequal adjacent sides, and the triangle formed by them and the diagonal connecting their two outside ends. Show that the isosceles triangle with the same base and perimeter has a larger area, so replacing the constructed triangle with the isosceles one will give a polygon with the same perimeter and a larger area.
Step 3: Show that a convex polygon with equal sides, fixed perimeter, and largest area, must have all its interior angles of the same measure. Do this by looking at two adjacent angles of unequal measure, and the three sides forming them. Connect a diagonal from the outside ends of the sides to form a quadrilateral. Show that the isosceles trapezoid formed by the diagonal and three sides of the same length as the sides of the polygon has the same perimeter and larger area than the quadrilateral constructed, so replacing the three given sides and two included angles with three sides of the same lengths and two equal included angles forms a polygon with the same perimeter and larger area. (The fact that, given the lengths of the sides, the quadrilateral with the largest area is cyclic, that is, all its vertices lie on a single circle, should help here.)
These three steps show that among all polygons with n sides and a fixed perimeter, the regular n-gon has the largest area.
|
|
 IP Logged IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register