 Author
Author |
Topic: Circle and string: find the area (Read 3367 times) |
|
D_S
Newbie


Posts: 6
|
 |
Circle and string: find the area
« on: Jan 4th, 2008, 12:10pm » |
 Quote Quote  Modify Modify
|
A string with length pi extends outward from the edge of a circle of radius 1. It is attached to a fixed point on the circumference of the circle. It cannot penetrate the circle and cannot be lifted up, so the string will wrap itself around the circle as it swings to the left or right. How much area can the string cover?
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Circle and string: find the area
« Reply #1 on: Jan 4th, 2008, 5:25pm » |
 Quote Quote  Modify Modify
|
5 3/6 3/6
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
D_S
Newbie


Posts: 6
|
 |
Re: Circle and string: find the area
« Reply #2 on: Jan 4th, 2008, 6:04pm » |
 Quote Quote  Modify Modify
|
You got it!
This was a bonus problem on a take-home calculus test I took. I found it very hard and didn't solve it in time, but afterward I worked out the following solution:
Consider a string of length pi attached to a regular n-gon with perimeter 2pi. For symmetry's sake, let the string be attached at the center of one of the sides. Now consider the area swept out by the string as it swings, fully extended, around the polygon to one side. If we can describe this area in terms of n, then we can solve the case of the circle by taking the limit as n approaches infinity (then multiplying by two, because the same area will be swept out if the string moves the other way).
Note the following:
*The string will start by sweeping out a quarter circle of radius pi regardless of the value of n. So for now, let's focus only on calculating the "conch shell" shaped area swept out after this quarter circle.
*The remaining area is made up of a series of semicircles of decreasing radius. If n is even, there are n/2 such semicircles, and if n is odd, there are (n-1)/2 of them.
*Each semicircle is 1/n the area of a full circle with the same radius.
*Label the radius of the first semicircle to be formed as r1, the next r2, and so on. rk is pi - ((2k-1)pi)/n.
*Since the perimeter of the polygon is fixed at 2pi, the sequence will always terminate at a point directly opposite the base of the string. That is, the string (with length pi) will cover half of the perimeter when it's wrapped around as far as it will go.
With this information, we can construct an appropriate sequence. Since in the end we're taking the limit as n approaches infinity, our answer will be the same whether we assume n is even or odd. So to make things easier we will assume it is even.
The area swept out after the quarter circle is described by (1/n)(pi)((r1)2 + (r2)2 + (r3)2 +...+(rn/2)2).
Plugging in our equation for rk, we get
(pi/n) times the sum from 1 to n/2 of (pi - ((2k-1)pi)/n)2.
Expanding that and factoring out pi2, we get
(pi3/n) times the sum from 1 to n/2 of 1 - (4k-2)/n + (4k2 - 4k + 1)/(n2).
Converting to closed form, we arrive at our function in terms of n:
f(n) = pi3((1/2) - ((n2/2)+2)/n2 + ((n3/6) + n2 + (n/3) +n + 1)/n3).
The limit as n approaches infinity of f(n) = (pi3)/6.
To get the combined area swept out by the string as it swings around to one side, add to this the area of the quarter circle: (pi3)/6 + (pi3)/4 = (5/12)pi3. Now multiply by 2 to get the total area that can be swept out by the string:
Area = (5/6)pi3.
Note: this result uses the closed form expansions sum(k=1 --> m)k = (m(m+1))/2 and sum(k=1 --> m)k2 = (m(m+1)(2m+1))/6
|
|
 IP Logged IP Logged |
|
|
|
balakrishnan
Junior Member
 

Gender: 
Posts: 92
|
 |
Re: Circle and string: find the area
« Reply #3 on: Jan 4th, 2008, 6:49pm » |
 Quote Quote  Modify Modify
|
It doesnt have to be that long.
Consider the circle to be centered at origin and the string to extend from (0,1) to (0,1+pi) at the initial point
Let us say the string wraps around the circle upto an angle t, then the remaining lenght of the string is pi-t.
This length is tangential to the circle. So the distance of the tip of the string from the center of the circle(origin) would be r=sqrt(1+(pi-t)^2)
Also the angle it makes with the y-axis=u=t+atan(pi-t)
du=(pi-t)^2/(1+(pi-t)^2) dt
So the required area while wrapping in the right side of the circle would be \int_{u} r^2 du/2
=\int_{0}^{pi} (pi-t)^2/2 dt
=pi^3/6
So the left hand side wrap is also pi^3/6
Also there is a semicircle formed by the string when it is not wrapping the circle at all.The area of this is
pi*pi^2/2=pi^3/2
So the total area is
pi^3/3+pi^3/2
=5*pi^3/6
|
|
 IP Logged IP Logged |
|
|
|
D_S
Newbie


Posts: 6
|
 |
Re: Circle and string: find the area
« Reply #4 on: Jan 4th, 2008, 8:35pm » |
 Quote Quote  Modify Modify
|
Nice! I had to wrack my brain to come up with a solution, but this is way more elegant.
|
|
 IP Logged IP Logged |
|
|
|
temporary
Full Member
  

Posts: 255
|
 |
Re: Circle and string: find the area
« Reply #5 on: Jan 24th, 2008, 9:51pm » |
 Quote Quote  Modify Modify
|
on Jan 4th, 2008, 5:25pm, ThudanBlunder wrote:5 3/6 3/6 |
|
Why wasn't pi hidden? How did you do that?
|
|
 IP Logged IP Logged |
My goal is to find what my goal is, once I find what my goal is, my goal will be complete.
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Circle and string: find the area
« Reply #6 on: Jan 24th, 2008, 10:24pm » |
 Quote Quote  Modify Modify
|
on Jan 24th, 2008, 9:51pm, temporary wrote:
Why wasn't pi hidden? How did you do that? |
|
Mind over matter, dear boy.
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Circle and string: find the area
« Reply #7 on: Jan 25th, 2008, 5:02pm » |
 Quote Quote  Modify Modify
|
 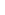  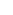 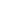           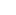   , and the hide feature is only able to hide text. , and the hide feature is only able to hide text.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register