 Author
Author |
Topic: Disappearing Black Squares (Read 1841 times) |
|
william wu
wu::riddles Administrator
    


Gender: 
Posts: 1291
|
 |
Disappearing Black Squares
« on: Dec 11th, 2007, 10:30am » |
 Quote Quote  Modify Modify
|
Consider an infinite square grid in which a finite number of squares are colored black, and the rest of the squares are white. We construct a new square grid according to the following rule: a square is black if and only if at least three of its four neighbors were black in the previous stage. If this process is repeated indefinitely, prove that eventually there are no black squares left.
|
|
 IP Logged IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Disappearing Black Squares
« Reply #1 on: Dec 11th, 2007, 10:56am » |
 Quote Quote  Modify Modify
|
It seems to me the bounding box the black squares can be in decreases in size from the outside in by two rows and two columns each step, until it's gone
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Disappearing Black Squares
« Reply #2 on: Dec 11th, 2007, 11:17am » |
 Quote Quote  Modify Modify
|
Not quite, towr -- at least not for a bounding box orthogonal to the grid. The edge of a solid rectangle is stable, it is only the corners which are eroded. However, if we consider a diagonal bounding box, rotated 45-degrees to grid, your observation holds, as every black square on the diagonal bound has at most two neighbors and so will be white in the next iteration
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Disappearing Black Squares
« Reply #3 on: Dec 11th, 2007, 2:11pm » |
 Quote Quote  Modify Modify
|
on Dec 11th, 2007, 11:17am, SMQ wrote: However, if we consider a diagonal bounding box, rotated 45-degrees to grid, your observation holds, as every black square on the diagonal bound has at most two neighbors and so will be white in the next iteration
--SMQ |
|
Nice proof 
|
| « Last Edit: Dec 11th, 2007, 2:12pm by Hippo » |
 IP Logged IP Logged |
|
|
|
temporary
Full Member
  

Posts: 255
|
 |
Re: Disappearing Black Squares
« Reply #4 on: Jan 23rd, 2008, 6:28pm » |
 Quote Quote  Modify Modify
|
Since there are infinite white squares, there are no black squares(there are, but they would be 0% of the board. Srn347 would have thoroughly enjoyed answering an infinity based riddle like this.
|
|
 IP Logged IP Logged |
My goal is to find what my goal is, once I find what my goal is, my goal will be complete.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Disappearing Black Squares
« Reply #5 on: Jan 24th, 2008, 12:48am » |
 Quote Quote  Modify Modify
|
on Jan 23rd, 2008, 6:28pm, temporary wrote:| Since there are infinite white squares, there are no black squares(there are, but they would be 0% of the board. Srn347 would have thoroughly enjoyed answering an infinity based riddle like this. |
|
And you're just as wrong as he used to be..
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Disappearing Black Squares
« Reply #6 on: Jan 24th, 2008, 5:23am » |
 Quote Quote  Modify Modify
|
I have thought about temporary ... is he srn347 or not. And now, he is citing him ... at least he have not attacked us so far 
Oh, he made its own thread srn347 sm347 ... so I am not first with this impression.
|
| « Last Edit: Jan 24th, 2008, 5:37am by Hippo » |
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: Disappearing Black Squares
« Reply #7 on: Jan 24th, 2008, 8:30am » |
 Quote Quote  Modify Modify
|
on Jan 23rd, 2008, 6:28pm, temporary wrote:| Since there are infinite white squares, there are no black squares(there are, but they would be 0% of the board. Srn347 would have thoroughly enjoyed answering an infinity based riddle like this. |
|
Consider a finite grid instead, formed by taking the original infinite grid, and, for each black square, identifying the 21*21 square with that black square at its centre. Take the union of all those 21*21 pieces, and, for each connected component, take the minimal orthogonal bounding rectangle. This may cause some previously disconnected components to become connected, so take bounding rectangles recursively until each connected component is an orthogonal rectangle. Discard the rest of the original grid, and iterate on the new, finite grid (it must be finite because each of the finite number of steps added a finite area to the grid). So long as none of the border cells turn black, the finite grid will behave the same way as that portion of the infinite grid.
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Disappearing Black Squares
« Reply #8 on: Jan 24th, 2008, 1:08pm » |
 Quote Quote  Modify Modify
|
on Jan 24th, 2008, 5:23am, Hippo wrote:| I have thought about temporary ... is he srn347 or not. |
|
He uses uncharacteristic words such as 'thoroughly' and 'ordinariness'. But surely an imposter would not make so many posts. Anyway, he should stay away from Putnam and confine himself to Easy, What Happened? and Why Am I a Snotty-nosed Little Dweeb?
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
temporary
Full Member
  

Posts: 255
|
 |
Re: Disappearing Black Squares
« Reply #9 on: Jan 24th, 2008, 10:45pm » |
 Quote Quote  Modify Modify
|
Is your rudeness an imitation of strength or intellect? More importantly, how was my answer wrong? x/infinity=0. Otherwise, how would the squares just disappear? Are the three of four neighbors counted vertical/horizontal, because I counted diagonal?
|
|
 IP Logged IP Logged |
My goal is to find what my goal is, once I find what my goal is, my goal will be complete.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Disappearing Black Squares
« Reply #10 on: Jan 25th, 2008, 12:29am » |
 Quote Quote  Modify Modify
|
on Jan 24th, 2008, 10:45pm, temporary wrote:| More importantly, how was my answer wrong? x/infinity=0. |
|
Considering infinity isn't a real number you can't divide by it.
Quote:| Otherwise, how would the squares just disappear? |
|
Because there is a process going on that changes the number of black squares in each step. It doesn't matter if the board is infinite or not, as rmsgrey has shown.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
temporary
Full Member
  

Posts: 255
|
 |
Re: Disappearing Black Squares
« Reply #11 on: Jan 25th, 2008, 6:59am » |
 Quote Quote  Modify Modify
|
on Jan 25th, 2008, 12:29am, towr wrote:
Considering infinity isn't a real number you can't divide by it.
Because there is a process going on that changes the number of black squares in each step. It doesn't matter if the board is infinite or not, as rmsgrey has shown. |
|
Infinity is hyperreal. And if the squares dissappear, it must be a paradox since logically they couldn't all be gone.
|
|
 IP Logged IP Logged |
My goal is to find what my goal is, once I find what my goal is, my goal will be complete.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Disappearing Black Squares
« Reply #12 on: Jan 25th, 2008, 7:40am » |
 Quote Quote  Modify Modify
|
on Jan 25th, 2008, 6:59am, temporary wrote:But we're not dealing with hyperreals.
Quote:| And if the squares dissappear, it must be a paradox since logically they couldn't all be gone. |
|
That clearly demonstrates you don't understand the problem; at all.
If you have 1 single square, then by the rules described in the opening post, in the next iteration it will be gone. There is no mystery or paradox as to why it's gone; it is stated in the rules that if it doesn't have at least 3 neighbours it won't be on the plane in the next iteration.
Look up cellular automata, or conway's game of life.
And you can consider yourself ignored from now on. Regardless of whether or not you're srn347, you're just as obtuse, annoying and willfully ignorant; and I've had enough. Goodbye, and I hope you grow out of.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Disappearing Black Squares
« Reply #13 on: Jan 25th, 2008, 5:15pm » |
 Quote Quote  Modify Modify
|
on Jan 25th, 2008, 6:59am, temporary wrote:
And if you bring in the hyperreals, x/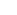 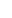 0 either. 0 either.
But in any case, probabilities and percentages are calculated using real numbers, not hyperreals, and 0% is not the same as none existing when infinite amounts are involved.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
temporary
Full Member
  

Posts: 255
|
 |
Re: Disappearing Black Squares
« Reply #14 on: Jan 25th, 2008, 5:53pm » |
 Quote Quote  Modify Modify
|
Ok. How would the second board have no black squares though? Perhaps infinitely small black squares.
|
|
 IP Logged IP Logged |
My goal is to find what my goal is, once I find what my goal is, my goal will be complete.
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Disappearing Black Squares
« Reply #15 on: Jan 25th, 2008, 5:58pm » |
 Quote Quote  Modify Modify
|
 Have you read the riddle? At each step, any black square that doesn't have 3 black neighbors (of 4 neighbors total, so diagonals are not considered neighbors) are removed. As rmsgrey has shown, eventually, this removes all the black squares. Have you read the riddle? At each step, any black square that doesn't have 3 black neighbors (of 4 neighbors total, so diagonals are not considered neighbors) are removed. As rmsgrey has shown, eventually, this removes all the black squares.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
temporary
Full Member
  

Posts: 255
|
 |
Re: Disappearing Black Squares
« Reply #16 on: Jan 25th, 2008, 8:21pm » |
 Quote Quote  Modify Modify
|
Oh, you keep repeating it. I thought it was only done once. If repeated indefinitely of coarse they will disappear. That is why they must be finite. If it was diagonal, it would have the same answer.
|
|
 IP Logged IP Logged |
My goal is to find what my goal is, once I find what my goal is, my goal will be complete.
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: Disappearing Black Squares
« Reply #17 on: Jan 26th, 2008, 10:01am » |
 Quote Quote  Modify Modify
|
on Jan 25th, 2008, 5:58pm, Icarus wrote:| As rmsgrey has shown, eventually, this removes all the black squares. |
|
Thanks for the credit, but all I've shown is that you can reduce it to a finite problem, the solution of which also solves the infinite case.
SMQ got there first with the solution to the infinite case.
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Disappearing Black Squares
« Reply #18 on: Jan 26th, 2008, 10:08am » |
 Quote Quote  Modify Modify
|
My apologies for the mis-attribution. I should have checked more carefully.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register