Author |
Topic: solve sqrt(x+1999·sqrt(x+1999·sqrt(...))) = x (Read 613 times) |
|
tony123
Junior Member
Posts: 61
|
 |
solve sqrt(x+1999·sqrt(x+1999·sqrt(...))) = x
« on: Nov 10th, 2007, 1:43am » |
 Quote  Modify
|
|
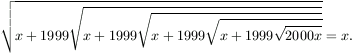
| « Last Edit: Nov 10th, 2007, 3:35pm by Grimbal » |
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender: 
Posts: 13730
|
|
Re: solve
« Reply #1 on: Nov 10th, 2007, 9:23am » |
Quote Modify
|
hmm.. not interested enough in your own problems to notice it's illegible?
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
JohanC
Senior Riddler
Posts: 460
|
|
V(x+1999V(x+1999V(x+1999V(x+1999V(2000x)))))=x  Sqrt1.png
« Reply #2 on: Nov 10th, 2007, 2:27pm » |
Quote Modify
|
on Nov 10th, 2007, 9:23am, towr wrote:| hmm.. not interested enough in your own problems to notice it's illegible? |
|
Looks like a problem with the transparent color in the gif format.
So, why not save it as png (which saves 300 bytes)?
(Waiting for somebody to change the thread's title ...)
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: solve sqrt(x+1999·sqrt(x+1999·sqrt(...))
« Reply #3 on: Nov 10th, 2007, 3:39pm » |
Quote Modify
|
Obvious solutions are 0 and 2000.
And considering that the whole sqrt(...) expression is concave, there can be no more than 2 real solutions.
The other solutions can be found among the zeros of a polynomial of degree 30, which I am too lazy to compute...
|
| « Last Edit: Nov 10th, 2007, 3:49pm by Grimbal » |
IP Logged |
|
|
|
anhkind
Newbie
Posts: 1
|
|
Re: solve sqrt(x+1999·sqrt(x+1999·sqrt(...))
« Reply #4 on: Nov 18th, 2007, 2:35am » |
Quote Modify
|
sqrt(x+1999·sqrt(x+1999·sqrt(...))) = x
<=> sqrt(x+1999*x)=x
<=> 2000x=x^2
<=> x=0 V x=2000
Solved.
|
|
IP Logged |
|
|
|
FiBsTeR
Senior Riddler
Gender:
Posts: 581
|
|
V(x+1999V(x+1999V(x+1999V(x+1999V(2000x)))))=x
« Reply #5 on: Nov 18th, 2007, 8:45am » |
Quote Modify
|
on Nov 18th, 2007, 2:35am, anhkind wrote:| sqrt(x+1999·sqrt(x+1999·sqrt(...))) = x |
|
The original equation was closed; you can't find all the solutions from this.
Aside: is it just a coincidence that the above equation yields solutions that are also solutions to the original equation?
|
| « Last Edit: Nov 18th, 2007, 8:46am by FiBsTeR » |
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: V(x+1999V(x+1999V(x+1999V(x+1999V(2000x)))))=x
« Reply #6 on: Nov 18th, 2007, 9:10am » |
Quote Modify
|
on Nov 18th, 2007, 8:45am, FiBsTeR wrote:| Aside: is it just a coincidence that the above equation yields solutions that are also solutions to the original equation? |
|
No.
If you start with sqrt(x+1999*x) and substitute the second x with x=sqrt(x+1999*x), x=0 or x=2000; then x=0 and x=2000 will remain solutions.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print