wu :: forums « wu :: forums - prove int » Welcome, Guest. Please Login or Register. Nov 28th, 2024, 9:48pm

RIDDLES SITE WRITE MATH! Home Help Search Members Login Register

wu :: forums    riddles    medium (Moderators: towr, Icarus, ThudnBlunder, Grimbal, SMQ, Eigenray, william wu)    prove int « Previous topic | Next topic » Pages: 1  Reply Notify of replies Send Topic Print    Author  Topic: prove int  (Read 1171 times) tony123 Junior Member     Posts: 61 prove int   « on: Sep 22nd, 2007, 1:15pm » Quote Modify cos (-89)+cos (-87) +.......+cos87 +cos 89 =csc 1       tan²(pi/7) +tan²(2pi/7) +tan²(3pi/7) =4 IP Logged Michael Dagg Senior Riddler     Gender: Posts: 500 Re: prove int   « Reply #1 on: Sep 22nd, 2007, 1:59pm » Quote Modify Anyone know what "prove int" means? -- I don't. IP Logged Regards, Michael Dagg Sameer Uberpuzzler Pie = pi * e     Gender: Posts: 1261 Re: prove int   « Reply #2 on: Sep 22nd, 2007, 2:03pm » Quote Modify on Sep 22nd, 2007, 1:59pm, Michael_Dagg wrote: Anyone know what "prove int" means? -- I don't.   tony123 has a bad habit of not providing good titles. Essentially his problems are prove LHS = RHS and in this case two problems... « Last Edit: Sep 22nd, 2007, 7:08pm by Sameer » IP Logged "Obvious" is the most dangerous word in mathematics. --Bell, Eric Temple Proof is an idol before which the mathematician tortures himself. Sir Arthur Eddington, quoted in Bridges to Infinity ThudnBlunder wu::riddles Moderator Uberpuzzler The dewdrop slides into the shining Sea     Gender: Posts: 4489 Re: prove int   « Reply #3 on: Sep 22nd, 2007, 6:51pm » Quote Modify on Sep 22nd, 2007, 1:59pm, Michael_Dagg wrote: Anyone know what "prove int" means? -- I don't. I would guess he means Prove It.   IP Logged THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you. srn437 Newbie the dark lord rises again....     Posts: 1 Re: prove int   « Reply #4 on: Sep 22nd, 2007, 10:01pm » Quote Modify Or maybe he meant prove intelligently. IP Logged tony123 Junior Member     Posts: 61 Re: prove int   « Reply #5 on: Sep 23rd, 2007, 1:43am » Quote Modify sory all   i mean prove  LHS = RHS  in  two problems   IP Logged Barukh Uberpuzzler     Gender: Posts: 2276 Re: prove int   « Reply #6 on: Sep 24th, 2007, 9:38am » Quote Modify The first is easy. The second looks much more difficult (and interesting).   BTW, shouldn't it be 21? « Last Edit: Sep 24th, 2007, 9:47am by Barukh » IP Logged Aryabhatta Uberpuzzler     Gender: Posts: 1321 Re: prove int   « Reply #7 on: Sep 24th, 2007, 1:14pm » Quote Modify For the second one:   If a = pi/7   then tan a, tan 2a, ..., tan 6a are roots of the polynomial   P(x) = x6 - 21x4 + 35x2 - 7   Sum of squares of roots of P(x) is 2*21.   Hence the required value is half of that = 21. IP Logged Barukh Uberpuzzler     Gender: Posts: 2276 Re: prove int   « Reply #8 on: Sep 25th, 2007, 9:56am » Quote Modify on Sep 24th, 2007, 1:14pm, Aryabhatta wrote: For the second one:   If a = pi/7   then tan a, tan 2a, ..., tan 6a are roots of the polynomial   P(x) = x6 - 21x4 + 35x2 - 7 Why? That's not obvious! « Last Edit: Sep 25th, 2007, 10:29am by Barukh » IP Logged pex Uberpuzzler     Gender: Posts: 880 Re: prove int   « Reply #9 on: Sep 25th, 2007, 10:34am » Quote Modify on Sep 25th, 2007, 9:56am, Barukh wrote: Why? That's not obvious! Yes, I do think it is. Repeatedly using the addition formula for tangents, we have   tan(7t) = tan t * [tan6t - 21tan4t + 35tan2t - 7] / [7tan6t - 35tan4t + 21tan2t - 1].   Now obviously, for t = pi/7, 2pi/7, ..., 7pi/7, we have tan(7t) = 0 and thus, these are the roots of   tan t * [tan6t - 21tan4t + 35tan2t - 7] = 0.   Put differently, tan(pi/7), tan(2pi/7), ..., tan(7pi/7) are the roots of   x * [x6 - 21x4 + 35x2 - 7] = 0.   Since tan(7pi/7) = 0, we may divide by x to leave an equation of which tan(pi/7), tan(2pi/7), ..., tan(6pi/7) are the roots:   x6 - 21x4 + 35x2 - 7 = 0. IP Logged Aryabhatta Uberpuzzler     Gender: Posts: 1321 Re: prove int   « Reply #10 on: Sep 25th, 2007, 11:32am » Quote Modify on Sep 25th, 2007, 9:56am, Barukh wrote: Why? That's not obvious!   It is not, but I didn't want to spoil it for others. pex has explained a way to get it. I did something slightly different, (but essentially same): tan 3a + tan 4a = 0 IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: prove int   « Reply #11 on: Sep 25th, 2007, 2:43pm » Quote Modify And here is how I did it: sin(7t)/[sin(t)cos6(t)] = 0.   Actually, at first I did sin(7t)/sin(t)=0, got a polynomial in x=cos2t, and solved for 1/cos2(k/7) = 24.   Actually, before that I expressed it in terms of = e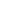/7, and "saw" that it was divisible by 14()=0.  But that is not a good solution. IP Logged Barukh Uberpuzzler     Gender: Posts: 2276 Re: prove int   « Reply #12 on: Sep 25th, 2007, 11:37pm » Quote Modify Nice!   The result may be generalized for any odd number 2n+1.   What about the first one? IP Logged tony123 Junior Member     Posts: 61 Re: prove int   « Reply #13 on: Sep 26th, 2007, 3:43am » Quote Modify on Sep 22nd, 2007, 1:15pm, tony123 wrote: cos (-89)+cos (-87) +.......+cos87 +cos 89 =csc 1       tan²(pi/7) +tan²(2pi/7) +tan²(3pi/7) =21 IP Logged Aryabhatta Uberpuzzler     Gender: Posts: 1321 Re: prove int   « Reply #14 on: Sep 26th, 2007, 11:45am » Quote Modify on Sep 25th, 2007, 11:37pm, Barukh wrote: What about the first one?   Isn't the "arithmetic series" summation of cosines well known?   cos 0 + cos h + cos 2h + ... + cos nh = (sin((n+1)h/2) * sin (nh/2))/sin(h/2)   (can be done easily using complex numbers I think) IP Logged Sameer Uberpuzzler Pie = pi * e     Gender: Posts: 1261 Re: prove int   « Reply #15 on: Sep 26th, 2007, 12:59pm » Quote Modify on Sep 26th, 2007, 11:45am, Aryabhatta wrote:   Isn't the "arithmetic series" summation of cosines well known?   cos 0 + cos h + cos 2h + ... + cos nh = (sin((n+1)h/2) * sin (nh/2))/sin(h/2)   (can be done easily using complex numbers I think)   Correct. You can use the Cis summation method nicely demonstrated by iyerkri   http://www.ocf.berkeley.edu/~wwu/cgi-bin/yabb/YaBB.cgi?board=riddles_put nam;action=display;num=1189578447 IP Logged "Obvious" is the most dangerous word in mathematics. --Bell, Eric Temple Proof is an idol before which the mathematician tortures himself. Sir Arthur Eddington, quoted in Bridges to Infinity Pages: 1  Reply Notify of replies Send Topic Print Forum Jump: ----------------------------- riddles -----------------------------  - easy => medium   - hard   - what am i   - what happened   - microsoft   - cs   - putnam exam (pure math)   - suggestions, help, and FAQ   - general problem-solving / chatting / whatever ----------------------------- general -----------------------------  - guestbook   - truth   - complex analysis   - wanted   - psychology   - chinese « Previous topic | Next topic »

Powered by YaBB 1 Gold - SP 1.4!
Forum software copyright © 2000-2004 Yet another Bulletin Board