wu :: forums « wu :: forums - Prime congruence... » Welcome, Guest. Please Login or Register. Nov 25th, 2024, 8:54am

RIDDLES SITE WRITE MATH! Home Help Search Members Login Register

wu :: forums    riddles    medium (Moderators: william wu, Icarus, SMQ, towr, Eigenray, ThudnBlunder, Grimbal)    Prime congruence... « Previous topic | Next topic » Pages: 1  Reply Notify of replies Send Topic Print    Author  Topic: Prime congruence...  (Read 1864 times) Michael Dagg Senior Riddler     Gender: Posts: 500 Prime congruence...   « on: Sep 17th, 2007, 3:15pm » Quote Modify With  p  prime, show that     (x + y)n = xn + yn (mod p)  iff   n  is a power of  p. IP Logged Regards, Michael Dagg pex Uberpuzzler     Gender: Posts: 880 Re: Prime congruence...   « Reply #1 on: Sep 18th, 2007, 1:29am » Quote Modify on Sep 17th, 2007, 3:15pm, Michael_Dagg wrote: With  p  prime, show that     (x + y)n = xn + yn (mod p)  iff   n  is a power of  p. Really?   (1 + 2)5 = 15 + 25 (mod 3) IP Logged Aryabhatta Uberpuzzler     Gender: Posts: 1321 Re: Prime congruence...   « Reply #2 on: Sep 18th, 2007, 1:31am » Quote Modify I think he meant for all x,y... IP Logged Barukh Uberpuzzler     Gender: Posts: 2276 Re: Prime congruence...   « Reply #3 on: Sep 18th, 2007, 2:37am » Quote Modify I guess it may be shown by using this property. IP Logged Michael Dagg Senior Riddler     Gender: Posts: 500 Re: Prime congruence...   « Reply #4 on: Sep 18th, 2007, 8:34am » Quote Modify It was meant as a polynomial congruence. IP Logged Regards, Michael Dagg JP05 Guest Re: Prime congruence...   « Reply #5 on: Sep 18th, 2007, 6:40pm » Quote Modify Remove I smell the binomial theorem. If you subtract the right from the left in that congruence you get (x+y)^n - x^n - y^n = sum(k=1 to n-1) B(n,k) x^k y^(n-k), where B(n,k) is n!/(k!(n-k)!).   Pondering this I think I could come up with a method by contradiction if I spent more time with it since it must be that if n is not a power of p then not all of the B(n,k) are divisible by p.   I am thinking. IP Logged Eigenray wu::riddles Moderator Uberpuzzler     Gender: Posts: 1948 Re: Prime congruence...   « Reply #6 on: Sep 18th, 2007, 7:00pm » Quote Modify Remark: For each prime p, define   a 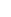p  b   <->  C(b,a) is not divisible by p.   It may be interesting to note that this is actually a partial order on the set of natural numbers.  Personally, I find it even more interesting that this partial order is actually useful!   Edit: Here C(b,a) = (bCa) = {b \choose a} = b!/(a!(b-a)!) is a binomial coefficient. « Last Edit: Sep 18th, 2007, 7:46pm by Eigenray » IP Logged JP05 Guest Re: Prime congruence...   « Reply #7 on: Sep 18th, 2007, 7:22pm » Quote Modify Remove Eigenray I understand your left side of that relation as partial order but what do you mean by C(b,a)? IP Logged JP05 Guest Re: Prime congruence...   « Reply #8 on: Sep 18th, 2007, 11:22pm » Quote Modify Remove Duh! Thanks. Your C(n,k) is my B(n,k). IP Logged Michael Dagg Senior Riddler     Gender: Posts: 500 Re: Prime congruence...   « Reply #9 on: Sep 19th, 2007, 11:19am » Quote Modify >  think I could come up with a method by contradiction     But that's not enough. IP Logged Regards, Michael Dagg Pages: 1  Reply Notify of replies Send Topic Print Forum Jump: ----------------------------- riddles -----------------------------  - easy => medium   - hard   - what am i   - what happened   - microsoft   - cs   - putnam exam (pure math)   - suggestions, help, and FAQ   - general problem-solving / chatting / whatever ----------------------------- general -----------------------------  - guestbook   - truth   - complex analysis   - wanted   - psychology   - chinese « Previous topic | Next topic »

Powered by YaBB 1 Gold - SP 1.4!
Forum software copyright © 2000-2004 Yet another Bulletin Board