 Author
Author |
Topic: Inscribed Triangle (Read 1956 times) |
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Inscribed Triangle
« on: Sep 3rd, 2007, 12:55am » |
 Quote Quote  Modify Modify
|
Given an arbitrary triangle, construct another triangle which is inscribed in the first and has the minimal perimeter.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
How about this.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Inscribed Triangle
« Reply #2 on: Sep 4th, 2007, 5:19am » |
 Quote Quote  Modify Modify
|
on Sep 3rd, 2007, 4:16pm, Eigenray wrote:
Bingo! 
Have you got a proof? What kind of a triangle will you get?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
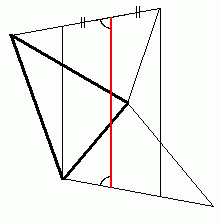
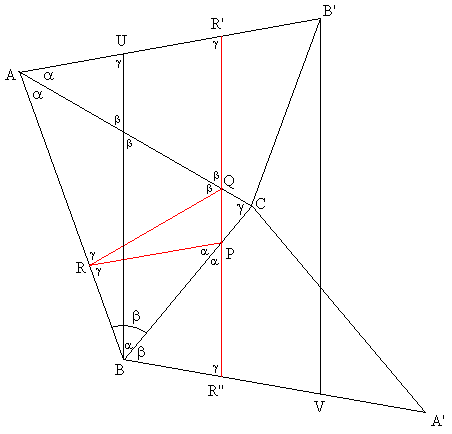
Let the triangle be ABC. I reasoned in 3 steps:
(1) Fix R on side AB, and Q on AC. How do you find P on BC minimizing QR + PQ + PR?
Reflect Q across BC to Q', and let P be the intersection of RQ' and BC.
(2) Fix R on side AB. How do you find P on BC and Q on AC minimizing QR + PQ + PR?
Reflect R across AC to R', and across BC to R''. Then QR+PQ+PR = R'Q+QP+PR''  R'R'', so let P,Q be the intersection of R'R'' with BC, AC, respectively R'R'', so let P,Q be the intersection of R'R'' with BC, AC, respectively
(3) How do you find P,Q, and R?
Reflect B across AC to B', and A across BC to A'. We must find R on AB minimizing R'R'' above. Subject to |R'B| = |RB| = |R''B|, it is clear(?) geometrically that |R'R''| is minimized when 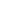 AR'R'' = AR'R'' = 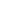 BR''R'. That is, R'R'' is parallel to the vertical lines BU and B'V in the diagram. Then |UR'| = |BR''| = |BR| = |R'B'| = |R''V|. So the desired line R'R'' is midway between BU and B'V. BR''R'. That is, R'R'' is parallel to the vertical lines BU and B'V in the diagram. Then |UR'| = |BR''| = |BR| = |R'B'| = |R''V|. So the desired line R'R'' is midway between BU and B'V.
The diagram assumes WLOG  + +  > >  /2, and that ABC is acute. (What happens if it's not?) /2, and that ABC is acute. (What happens if it's not?)
Can you show the following: the following triangles are all similar
ABC ~ AQR ~ PBR ~ PQC
in the ratio 1 : cos : cos : cos : cos : cos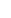 ? ?
Thus |PQR| = (1 - cos2 - cos2 - cos2 - cos2 - cos2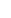 )*|ABC|, )*|ABC|,
and the minimal perimeter is
PQ+QR+RP = a cos + b cos + b cos + c cos + c cos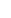
= (a sin )(b sin )(b sin )(c sin )(c sin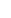 )/ K )/ K
= 2 K/R = 8 K2/(abc),
where K = |ABC|, and 2R = a/sin is the diameter of the circumscribed triangle. is the diameter of the circumscribed triangle.
Amusingly, the perimeter of PQR is
2 * sin * sin * sin * c, * c,
which is "dual" to the area of the original triangle
1/2 * a * b * sin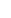 . .
Is there a deeper reason for this?
on Sep 4th, 2007, 5:19am, Barukh wrote:| What kind of a triangle will you get? |
|

|
| « Last Edit: Sep 4th, 2007, 8:39pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Inscribed Triangle
« Reply #4 on: Sep 4th, 2007, 9:23pm » |
 Quote Quote  Modify Modify
|
Help me out here, guys. Shouldn't the inscribed triange be required to touch all three sides of the enclosing triangle? Otherwise, the answer is a single point with perimeter zero.
If the inscribed triangle is required to touch all three sides of the enclosing triangle, I can construct such a triangle with perimeter equal to twice the length of a shortest side of the enclosing triangle, which perimeter is shorter than the one in Eigenray's picture. What am I missing?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Inscribed Triangle
« Reply #5 on: Sep 4th, 2007, 9:56pm » |
 Quote Quote  Modify Modify
|
on Sep 4th, 2007, 9:23pm, ecoist wrote:| Help me out here, guys. Shouldn't the inscribed triange be required to touch all three sides of the enclosing triangle? Otherwise, the answer is a single point with perimeter zero. |
|
That's hardly inscribed!
Quote:| If the inscribed triangle is required to touch all three sides of the enclosing triangle, I can construct such a triangle with perimeter equal to twice the length of a shortest side of the enclosing triangle, which perimeter is shorter than the one in Eigenray's picture. What am I missing? |
|
Is this for an obtuse triangle? It seems my construction goes horribly wrong in this case. If it is obtuse, maybe the solution is to take the shortest altitude?
|
|
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Inscribed Triangle
« Reply #6 on: Sep 4th, 2007, 10:12pm » |
 Quote Quote  Modify Modify
|
Sorry, I'm still lost, Eigenray! Your inscribed triangle touches all three sides of the enclosing triangle, exactly as I meant. And yes, my construction is obtuse. Oops! You meant the enclosing triangle could be obtuse. My construction doesn't care; my constructed inscribed triangle is always obtuse.
|
| « Last Edit: Sep 4th, 2007, 10:18pm by ecoist » |
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Inscribed Triangle
« Reply #7 on: Sep 5th, 2007, 5:01am » |
 Quote Quote  Modify Modify
|
Nice solution, Eigenray! Although I had a different one in mind.
Quote:
Connect the points A, P; B, Q; C, R. What do you get? And why?
on Sep 4th, 2007, 10:12pm, ecoist wrote:| Oops! You meant the enclosing triangle could be obtuse. My construction doesn't care; my constructed inscribed triangle is always obtuse. |
|
Are you saying you can beat Eigenray’s solution in case the enclosing triangle is acute?

on Sep 4th, 2007, 9:56pm, Eigenray wrote:| Is this for an obtuse triangle? It seems my construction goes horribly wrong in this case. If it is obtuse, maybe the solution is to take the shortest altitude? |
|

|
|
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Inscribed Triangle
« Reply #8 on: Sep 5th, 2007, 9:32am » |
 Quote Quote  Modify Modify
|
Quote:| Are you saying you can beat Eigenray’s solution in case the enclosing triangle is acute? |
|
I'm saying exactly that unless I miss-understand the meaning of "triangle inscribed in a triangle".
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Inscribed Triangle
« Reply #9 on: Sep 5th, 2007, 9:50am » |
 Quote Quote  Modify Modify
|
on Sep 5th, 2007, 9:32am, ecoist wrote:| I'm saying exactly that unless I miss-understand the meaning of "triangle inscribed in a triangle". |
|
Could you please provide an example?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Inscribed Triangle
« Reply #10 on: Sep 5th, 2007, 10:05am » |
 Quote Quote  Modify Modify
|
on Sep 4th, 2007, 10:12pm, ecoist wrote:| Your inscribed triangle touches all three sides of the enclosing triangle, exactly as I meant. |
|
I meant that civilized people would not call a point an inscribed triangle.
on Sep 5th, 2007, 5:01am, Barukh wrote:| Connect the points A, P; B, Q; C, R. What do you get? |
|
Well, that was unexpected! Drop perpendiculars AP, BQ, CR. Now, BR = a cos , BP = c cos , BP = c cos , and , and 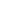 RBP = RBP =  , so RP = b cos , so RP = b cos , and ABC is similar to PBR. Similarly, we get , and ABC is similar to PBR. Similarly, we get 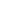 BRP = BRP = 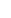 = = 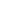 ARQ, ARQ, 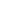 AQR = AQR =  = PQC, and = PQC, and 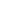 RPB = RPB =  = = 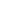 QPC. QPC.
So a light beam emitted from P towards Q will reflect around and around in triangle PQR. This is the same as the triangle previously constructed.
|
| « Last Edit: Sep 5th, 2007, 10:17am by Eigenray » |
 IP Logged IP Logged |
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Inscribed Triangle
« Reply #11 on: Sep 5th, 2007, 10:28am » |
 Quote Quote  Modify Modify
|
Quote:| Could you please provide an example? |
|
Gladly, Barukh! Using Eigenray's figure, my triangle is BCP. Although this triangle is degenerate, it lies within Eigenray's black triangle and touches all three sides of that triangle. Its perimeter is clearly 2|BC|, which is less than the perimeter of PQR.
Why is this example illegitimate?
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Inscribed Triangle
« Reply #12 on: Sep 5th, 2007, 11:17am » |
 Quote Quote  Modify Modify
|
on Sep 5th, 2007, 10:28am, ecoist wrote:Its perimeter is clearly 2|BC|, which is less than the perimeter of PQR.
Why is this example illegitimate? |
|
Leaving aside the legitimity of this triangle, its perimeter is more than Eigenray's solution, which for example follows from this remark:
on Sep 4th, 2007, 7:34pm, Eigenray wrote:Amusingly, the perimeter of PQR is
2 * sin * sin * sin * c, * c, |
|
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Inscribed Triangle
« Reply #13 on: Sep 5th, 2007, 1:03pm » |
 Quote Quote  Modify Modify
|
From Eigenray's explanation it seems the triangle with smallest perimeter is a orthic triangle - is that the right term? the triangle formed by the feet of the altitudes . This shows that for an obtuse triangle the minimum permiter triangle i.e. the orthic triangle lies outside the triangle, so there has to be another triangle?? . I still don't have my own proof. Working on it!!
|
| « Last Edit: Sep 5th, 2007, 1:04pm by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Inscribed Triangle
« Reply #14 on: Sep 5th, 2007, 4:20pm » |
 Quote Quote  Modify Modify
|
How stupid of me! Thanks, Barukh. I had a mental cramp that no perimeter of an inscribed triangle could be less than 2|BC|.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
on Sep 5th, 2007, 10:05am, Eigenray wrote:| Well, that was unexpected! |
|
Exactly! This triangle is called orthic, as Sameer pointed out rightly.
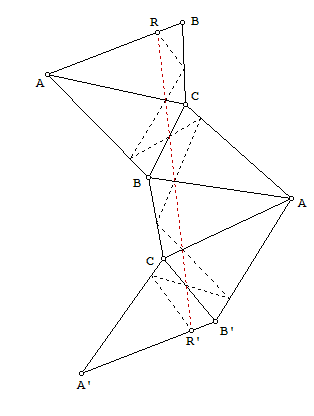
Eigenray, if we continue your drawing for another 3 triangle, the picture we get is almost self-explanatory (where the solution is drawn is dashed line): segments AB and A’B’ are parallel (why?), RR’ is a straight line (why?), and any other line connecting corresponding points will have a greater length (solution by H.A.Schwarz).
on Sep 5th, 2007, 1:03pm, Sameer wrote:| This shows that for an obtuse triangle the minimum permiter triangle i.e. the orthic triangle lies outside the triangle, so there has to be another triangle?? . I still don't have my own proof. Working on it!! |
|

|
| « Last Edit: Sep 6th, 2007, 4:59am by Barukh » |
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Inscribed Triangle
« Reply #16 on: Sep 6th, 2007, 9:48pm » |
 Quote Quote  Modify Modify
|
Interesting. 5 reflections of the triangle!! How do you start with point R? As in the internal traces - how do you start with it? Is there a way to work out this method based on Eigenray's equation? e.g. equation 1 translates to reflection, etc...
|
|
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Inscribed Triangle
« Reply #17 on: Sep 7th, 2007, 2:00am » |
 Quote Quote  Modify Modify
|
on Sep 6th, 2007, 9:48pm, Sameer wrote:| Is there a way to work out this method based on Eigenray's equation? e.g. equation 1 translates to reflection, etc... |
|
In his derivation, Eigenray proved the mirror property of the orthic triangle: its sides form equal angles with the corresponding side of the enclosing triangle. Following this, is it clear that a reflection of orthic triangle in any side will produce a pair of parallel segments. This, in fact, determines uniquely a sequence of reflections, if we want to get a straight line of the sides of the orthic triangle (Eigneray used 2 such reflections). Now, it is left to notice that after the 5th reflection we get a pair of parallel lines of the enclosing triangle (this fact is still to be proved).
|
|
 IP Logged IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
    

Gender: 
Posts: 1321
|
 |
Re: Inscribed Triangle
« Reply #18 on: Sep 7th, 2007, 3:48pm » |
 Quote Quote  Modify Modify
|
I believe this is called as Fagnano's problem which Fagnano had solved using Calculus.
(See the name of the image which Barukh attached  ) )
Schwartz was the first to give the elegant proof by mirroring.
Sorry for adding nothing to this thread 
|
|
 IP Logged IP Logged |
|
|
|
Sameer
Uberpuzzler
    

Pie = pi * e
Gender: 
Posts: 1261
|
 |
Re: Inscribed Triangle
« Reply #19 on: Sep 7th, 2007, 4:01pm » |
 Quote Quote  Modify Modify
|
Wow I didn't know this problem had a name!!  I googled and got this famous site!! I googled and got this famous site!!
http://www.cut-the-knot.org/Curriculum/Geometry/Fagnano.shtml
|
| « Last Edit: Sep 7th, 2007, 4:01pm by Sameer » |
 IP Logged IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
ecoist
Senior Riddler
   

Gender: 
Posts: 405
|
 |
Re: Inscribed Triangle
« Reply #20 on: Sep 7th, 2007, 6:57pm » |
 Quote Quote  Modify Modify
|
Sameer wrote:
Quote:| after the 5th reflection we get a pair of parallel lines of the enclosing triangle (this fact is still to be proved) |
|
In the figure, rewrite the middle A and B as A'' and B'', and write the middle C as C'. Then the figures ABCB''A'' and A'B'C'A''B'' are congruent. Hence the angles between the lines AB and A''B'' and that between A'B' and A''B'' are equal; whence AB and A'B' are parallel.
This suggests that the choice of R can vary, as long as the dotted red line stays inside the figure.
Oops! Goofed again! That dotted red line must pass through R'' on A''B'' as well as R' on A'B'! Since moving R right/left causes R'' to move left/right, there is only one choice for R.
So what happens if angle ABC is greater than 90 degrees, when there is no R? Is Eigenray's suggestion, an altitude, the solution for obtuse triangles?
|
| « Last Edit: Sep 7th, 2007, 8:35pm by ecoist » |
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Inscribed Triangle
« Reply #21 on: Sep 7th, 2007, 11:07pm » |
 Quote Quote  Modify Modify
|
on Sep 7th, 2007, 6:57pm, ecoist wrote:| Oops! Goofed again! That dotted red line must pass through R'' on A''B'' as well as R' on A'B'! Since moving R right/left causes R'' to move left/right, there is only one choice for R. |
|
Yes, you got it right.
Quote:| So what happens if angle ABC is greater than 90 degrees, when there is no R? Is Eigenray's suggestion, an altitude, the solution for obtuse triangles? |
|
Exactly.
|
|
 IP Logged IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
    

I am no special. I am only passionately curious.
Gender: 
Posts: 1001
|
 |
Re: Inscribed Triangle
« Reply #22 on: Sep 8th, 2007, 2:30am » |
 Quote Quote  Modify Modify
|
on Sep 7th, 2007, 6:57pm, ecoist wrote:| So what happens if angle ABC is greater than 90 degrees, when there is no R? Is Eigenray's suggestion, an altitude, the solution for obtuse triangles? |
|
From cut-the-knot,
Excerpt :
In obtuse or right triangles, however, no inscribed proper (with distinct vertices) triangle attains the minimum possible perimeter. There exist triangles whose perimeter is arbitarily close to twice the length of the shortest altitude but no proper triangle attains this value.
-- AI
P.S -> So, i guess one has to prove the non-existence here.
|
| « Last Edit: Sep 8th, 2007, 2:30am by TenaliRaman » |
 IP Logged IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: Inscribed Triangle
« Reply #23 on: Sep 9th, 2007, 6:33pm » |
 Quote Quote  Modify Modify
|
For any triangle in that triangle, there is one in that one with smaller perimeter. It would have to have perimeter of zero which wouldn't even be a triangle. So there is no answer.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Inscribed Triangle
« Reply #24 on: Sep 9th, 2007, 9:43pm » |
 Quote Quote  Modify Modify
|
on Sep 9th, 2007, 6:33pm, srn347 wrote:| For any triangle in that triangle, there is one in that one with smaller perimeter. It would have to have perimeter of zero which wouldn't even be a triangle. So there is no answer. |
|
Let me remind you that "inscribed triangle" means a triangle touching all 3 sides of the original triangle. Therefore, it cannot have a zero perimeter.
If you want to make your argument stronger, please take the figures posted by Eigenray or me and try to show an inscribed triangle with smaller perimeter.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register