 Author
Author |
Topic: Maximum number of 'levels' in a graph (Read 520 times) |
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Maximum number of 'levels' in a graph
« on: Aug 2nd, 2007, 6:15am » |
 Quote Quote  Modify Modify
|
Let's define a level as the set composed of all the nodes of a graph that can be reached from a given node in the same number of steps.
Then how many distinct 'levels' can there be at most for a graph with n nodes?
In a more mathematical notation: if we have levels
Li(r) = { x | Ri(r,x)}
What is the maximum k for which we can have all Li(r) and Lj(r) distinct for some r and i < j  k k
Obviously there are at most 2n different possible Li's, but can k be that big?
|
| « Last Edit: Aug 2nd, 2007, 6:17am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Maximum number of 'levels' in a graph
« Reply #1 on: Aug 2nd, 2007, 7:47am » |
 Quote Quote  Modify Modify
|
As I understand the problem, an upper bound would be n2+1. There are n starting nodes, and the distance between nodes ranges from 0 to n-1. One more for the empty set. It is easy to see that even that maximum cannot be reached for n>1.
I think n(n+1)/2 can be reached.
In your definition, does the set include those nodes that can be otherwise reached in less than i steps?
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Maximum number of 'levels' in a graph
« Reply #2 on: Aug 2nd, 2007, 9:02am » |
 Quote Quote  Modify Modify
|
on Aug 2nd, 2007, 7:47am, Grimbal wrote:| In your definition, does the set include those nodes that can be otherwise reached in less than i steps? |
|
No, they're only in the set if they can be reached in exactly i steps.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Maximum number of 'levels' in a graph
« Reply #3 on: Aug 2nd, 2007, 9:36am » |
 Quote Quote  Modify Modify
|
It seems you can get at least (n-1)2+1 levels, if you take a string of nodes of which the last two elements are connected to the start.
That the best I've found.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Maximum number of 'levels' in a graph
« Reply #4 on: Aug 2nd, 2007, 2:58pm » |
 Quote Quote  Modify Modify
|
on Aug 2nd, 2007, 9:02am, towr wrote:
No, they're only in the set if they can be reached in exactly i steps. |
|
I expected "yes, I include all nodes that can be reached in exactly i steps" or "no, I include only nodes that can be reached in i steps an not in less".
Let's take an example. If you have a list of 7 nodes, r is the 3rd and i increases from 0, do you get:
--x----
-x-x---
x---x--
-----x-
------x
or
--x----
-x-x---
x-x-x--
-x-x-x-
x-x-x-x
?
Anyway, it seems to be the 2nd option. And it is a bit messy to count.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Maximum number of 'levels' in a graph
« Reply #5 on: Aug 2nd, 2007, 3:28pm » |
 Quote Quote  Modify Modify
|
on Aug 2nd, 2007, 2:58pm, Grimbal wrote:| I expected "yes, I include all nodes that can be reached in exactly i steps" or "no, I include only nodes that can be reached in i steps an not in less". |
|
I would hope my reply would be consider equivalent to the former.
Li(r) = { x | Ri(r,x)}
R0(r,r)
R1(r,x) iff R(r,x)
i>1: Ri(r,x) iff 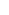 v R(r,v) v R(r,v) 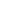 Ri-1(v,x) Ri-1(v,x)
R(r,x) iff there is a connection from r to x.
Quote:Let's take an example. If you have a list of 7 nodes, r is the 3rd and i increases from 0, do you get:
--x----
-x-x---
x---x--
-----x-
------x
|
|
If the connection are uni-directional away from the third node, yes.
If they are bidirectional you'd have:
Quote:
--x----
-x-x---
x-x-x--
-x-x-x-
x-x-x-x
|
|
I suppose I left it in the middle a bit whether it should be a directed graph or not. Of course, an undirected graph is really just a directed graph with symmetric connectivity.
Quote:| Anyway, it seems to be the 2nd option. And it is a bit messy to count. |
|
Yes, that's why I posted it here.
It came up in programming project I'm working on, and I was worried it might be exponential or at least much worse than quadratic.
And it seemed to make an interesting puzzle.
|
| « Last Edit: Aug 2nd, 2007, 3:31pm by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register