Author |
Topic: find the dominant poles configurations (Read 491 times) |
|
gkwal
Newbie
Posts: 25
|
 |
find the dominant poles configurations
« on: Jul 16th, 2007, 9:46pm » |
 Quote  Modify
|
Nine poles of height 1,2…9 are placed in a line in random order. A pole is called dominant if it is taller than the pole immediately to the left of it, or if it is the pole farthest to the left. Count the number of possible orderings in which there are exactly 2 dominant poles.
|
|
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender: 
Posts: 13730
|
|
Re: find the dominant poles configurations
« Reply #1 on: Jul 17th, 2007, 7:38am » |
Quote Modify
|
You have exactly two dominant poles if the sequence is partitioned in exactly three descending parts with a jump from one part to the next.
So, I suppose, the number of ways you can make three partitions (with regard for order between them, but not within), minus the number of ways you can make two, minus 1. Right? Something along those lines, certainly..
Now what was that partition counting function again.
|
| « Last Edit: Jul 17th, 2007, 8:10am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
|
Re: find the dominant poles configurations
« Reply #2 on: Jul 17th, 2007, 10:19am » |
Quote Modify
|
on Jul 17th, 2007, 7:38am, towr wrote:| You have exactly two dominant poles if the sequence is partitioned in exactly three descending parts with a jump from one part to the next. |
|
You did mean two descending parts, didn't you?
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: find the dominant poles configurations
« Reply #3 on: Jul 17th, 2007, 10:23am » |
Quote Modify
|
on Jul 17th, 2007, 10:19am, rmsgrey wrote:| You did mean two descending parts, didn't you? |
|
No, three.
The start of the second dominates the end of the first, the start of the third dominates the end of the second, the rest dominate nothing.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: find the dominant poles configurations
« Reply #4 on: Jul 17th, 2007, 10:30am » |
Quote Modify
|
on Jul 17th, 2007, 10:23am, towr wrote:
No, three.
The start of the second dominates the end of the first, the start of the third dominates the end of the second, the rest dominate nothing.
|
|
The start of the first is the leftmost pole, so also dominant
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: find the dominant poles configurations
« Reply #5 on: Jul 17th, 2007, 10:34am » |
Quote Modify
|
on Jul 17th, 2007, 10:30am, rmsgrey wrote:
The start of the first is the leftmost pole, so also dominant |
|
Ah sorry, I missed/ignored "or if it is the pole farthest to the left".
So yeah, then it's two, and a lot simpler allround.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Whiskey Tango Foxtrot
Uberpuzzler
Sorry Goose, it's time to buzz a tower.
Gender:
Posts: 1672
|
|
Re: find the dominant poles configurations
« Reply #6 on: Jul 17th, 2007, 12:53pm » |
Quote Modify
|
Much simpler, towr. A very fun little problem.
If I didn't make any arithmetic errors  I get 255.
|
|
IP Logged |
"I do not feel obliged to believe that the same God who has endowed us with sense, reason, and intellect has intended us to forgo their use." - Galileo Galilei
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: find the dominant poles configurations
« Reply #7 on: Jul 17th, 2007, 1:30pm » |
Quote Modify
|
Seems about right 29/2 - 1, and in general 2K/2 - 1, and more generally still, errm.. MK/M! - (M-1)K/(M-1)! ?
I'm sure someone will correct me if I'm wrong..
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: find the dominant poles configurations
« Reply #8 on: Jul 17th, 2007, 1:49pm » |
Quote Modify
|
Isn't it equivalent to the 9-letter case of this problem? If it is, then I'm pretty sure there are in general Sum from k = 1 to n - 1 of (C(n,k) - 1) = 2^n - n - 1 orderings, and so specifically 502 for this problem.
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
Whiskey Tango Foxtrot
Uberpuzzler
Sorry Goose, it's time to buzz a tower.
Gender:
Posts: 1672
|
|
Re: find the dominant poles configurations
« Reply #9 on: Jul 17th, 2007, 2:03pm » |
Quote Modify
|
I thought it was      from   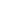where n is the number of digits from the right-hand side available for switching. This still seems very correct to me. I believe this produces a similar result to towr's, though I would think he meant 27-1 while SMQ's answer is on the order of 28.
|
|
IP Logged |
"I do not feel obliged to believe that the same God who has endowed us with sense, reason, and intellect has intended us to forgo their use." - Galileo Galilei
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: find the dominant poles configurations
« Reply #10 on: Jul 17th, 2007, 2:17pm » |
Quote Modify
|
As noted above, the leftmost pole is always dominant, so we're looking for all the sequences which are monotonic decreasing (left-to-right) except for a single break, yes?
If the break is after position k, 1 <= k < n, consider the monotonic decreasing subsequence of poles 1 through k. This subsequence can consist of any k of the n poles except for the k tallest poles (in which case it would be impossible to have a break); so the number of ways to construct two monotonic sequences with a break after position k is C(n,k) - 1.
Then the number of ways to construct a sequence of length n which is monotonic except for a single break is Sum from k=1 to n-1 of (C(n,k) - 1) which is 2n - n - 1.
That reasoning worked to lead me to the right answer to the problem I linked above on Sir Col's Project Euler site, so I'm fairly certain it's correct.
And a quick program to check all 362880 permutations of 9 poles counts 502 with exactly 2 dominant.
--SMQ
|
| « Last Edit: Jul 17th, 2007, 2:18pm by SMQ » |
IP Logged |
--SMQ
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: find the dominant poles configurations
« Reply #11 on: Jul 17th, 2007, 2:20pm » |
Quote Modify
|
on Jul 17th, 2007, 2:03pm, Whiskey Tango Foxtrot wrote:| I thought it was from 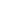where n is the number of digits from the right-hand side available for switching. This still seems very correct to me. I believe this produces a similar result to towr's, though I would think he meant 27-1 |
|
You have 9 elements in 1 of 2 (descending) groups (29), and the groups are in one of two positions (divide by 2!), and then we have the case where there's really only one descending group, which we subtract from it (-1).
So I don't see how you'd get 27-1 from my approach. (27=128, 28=256, 29=512)
I'll have to think a bit on your approach.
Oh, never mind.. I'll have another look tomorrow when it's not so late; SMQ's probably right anyway.
|
| « Last Edit: Jul 17th, 2007, 2:27pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: find the dominant poles configurations
« Reply #13 on: Jul 18th, 2007, 8:44am » |
Quote Modify
|
on Jul 17th, 2007, 2:20pm, towr wrote:| Oh, never mind.. I'll have another look tomorrow when it's not so late; SMQ's probably right anyway. |
|
There are a couple of problems with your solution:
1) the two groups are ordered, so you shouldn't be dividing by two - stick with 29=512 for your first estimate.
2) there's more than one way to get the single descending sequence - in fact, there are 10, one for each length of the first group (0 to 9 inclusive) - in the case that all of the first group are greater than each of the second group. 512-10=502
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print