Author |
Topic: Dijkstra, AMM and geometry (Read 7013 times) |
|
Aryabhatta
Uberpuzzler
Gender: 
Posts: 1321
|
A geometry problem which interested Dijkstra, from AMM 1998.
(AMM = American Mathematics Monthly)
In the figure below,
If AD + DF equals AB + BF
Show that
AE + EF = AC + CF
|
| « Last Edit: Apr 19th, 2007, 10:58am by Aryabhatta » |
 IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
 |
Re: Dijkstra, AMM and geometry
« Reply #1 on: Apr 20th, 2007, 8:26am » |
 Quote  Modify
|
One observation which may lead nowhere: A and F are focii of an ellipse, and B and D points on the perimeter.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
Here’s a nice solution I learned elsewhere.
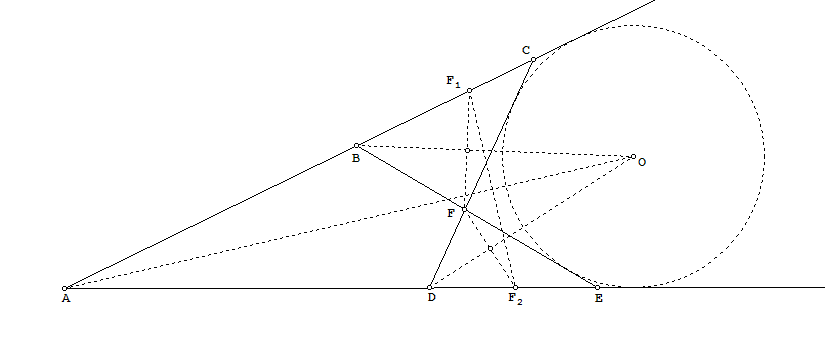
If we can show that, under given conditions, there exists a circle touching four lines AC, AD, CD, BE (prolonged, if needed – see the drawing), that the statement of the problem will follow (why?)
To show that such a circle indeed exists, consider the ex-circles of triangles ACD and ABE (the ex-circle of a triangle is a circle tangent to 2 of its sides internally and one externally).
The center O1 of the ex-circle of ACD is the intersection of angle bisectors A and CDE.
The center O2 of the ex-circle of ABE is the intersection of angle bisectors A and CBE.
Now, consider the triangle FF1F2, where F1, F2 are chosen on corresponding lines such that BF1 = BF, DF2 = DF. Since AF1 = AB+BF1 = AB+BF = AD+DF = AD+DF2 = AF2, we get that all three triangles F1AF2, F1BF, F2DF are isosceles.
Therefore, the bisectors of angles A, CBE, CDE coincide with the bisectors of corresponding segments F1F2, FF1, FF2. But the latter 3 bisectors are concurrent, since they define the center of the circumcircle of the triangle F1FF2. Thus, O1 and O1 coincide.
Finally, the ex-circles of triangles ACD and ABE also coincide, since they touch the same two lines and are centered at the same point. But now it follows that this circle touches all four needed lines!
|
| « Last Edit: Apr 27th, 2007, 10:03am by Barukh » |
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: Dijkstra, AMM and geometry
« Reply #3 on: Apr 27th, 2007, 12:49pm » |
Quote Modify
|
Interesting solution Barukh!
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Dijkstra, AMM and geometry
« Reply #4 on: Apr 27th, 2007, 11:10pm » |
Quote Modify
|
Thanks. Some interesting results about this theorem:
1. It is attributed to Australian mathematician M. L. Urguhart who discovered the result in 1960s while "considering some of the fundamental concepts of the theory of special relativity" (!)
2. The result was proved as early as 1841 by English mathematician De Morgan.
3. The theorem has the following nice equivalent statement (partly spotted by rsmgrey): If C and E are points on an ellipse with foci A and F, then points of intersection AC, EF and AE, CF lie on a confocal ellipse".
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print