Author |
Topic: A Non-overlapping Circle Puzzle (Read 9577 times) |
|
K Sengupta
Senior Riddler
Gender: 
Posts: 371
|
 |
A Non-overlapping Circle Puzzle
« on: Nov 16th, 2006, 12:11am » |
 Quote  Modify
|
What is the radius of the smallest circle that can enclose all 52 non-overlapping circle of an ordinary deck of playing cards?
For the purposes of the problem, assume that the smaller dimension of the cards is 5 and the largest is 7.
|
| « Last Edit: Nov 16th, 2006, 4:40am by K Sengupta » |
 IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #2 on: Nov 16th, 2006, 5:23pm » |
Quote Modify
|
An obvious lower bound is sqrt(52*5*7/pi) ~ 28.58 24.07.
Nearly as obvious is the upper bound sqrt((4*7)2 + (13*5)2)/2 ~ 35.39.
|
| « Last Edit: Nov 17th, 2006, 8:01pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #3 on: Nov 16th, 2006, 9:28pm » |
Quote Modify
|
Is it 30.166?
|
|
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
K Sengupta
Senior Riddler
Gender:
Posts: 371
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #4 on: Nov 16th, 2006, 10:29pm » |
Quote Modify
|
According to the one line solution in the puzzle periodical where I found this problem ; the answer is 30.7774 units.
I am looking for an analytic proceedure leading to the said solution.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #5 on: Nov 17th, 2006, 9:03am » |
Quote Modify
|
I suspect no one knows an effective way to compute a provably minimal
circle which contains 52 nonoverlapping 5x7 rectangles. But if you
make the simplifying assumption that all cards are have parallel edges,
then this may be doable. No, let me be more precise: it may be doable
if you assume that in the direction of one set of card edges (we'll
call this direction the "columns") all the cards in a column have the same
orientation.
If we draw coordinate axes in the natural way, then all you need to know
is the x-coordinates v_i of the left edges of the columns that contain
vertically-oriented cards, and the x-coordinates h_i of the left edges
of the horizontally-oriented columns. Note that we will have
v_i >= v_{i-1} + 5, h_i >= h_{i-1} + 7, and for all i and j
v_i - h_j >= 7 or <= 0, and h_i - v_j >= 5 or <= 0.
We might also let w_i and k_i denote the vertical lengths of certain obvious
line segments, so that we have the constraints v_i^2 + w_i^2 <=r and
(v_i +5)^2 + w_i^2 <=r and similarly h_i^2 + k_i^2 <=r and
(h_i +7)^2 + k_i^2 <=r, and the number-of-card constraint
sum(floor( 2 w_i / 7 )) + sum(floor( 2 k_i / 5 )) >= 52
So you have a bunch of real variables v_i, h_i, w_i, k_i, and r, and
you have a bunch of inequalities that describe a region in this space,
and on that domain you wish to minimize r . That would just be
Lagrange multipliers or something.
(Hm, I guess in practice you would need to consider separately the
cases in which there are 0, 1, 2, ... v's and 0,1,2,... h's.
Obviously there are no more than 53^2 such combinations to try.)
Of course it would be quite laborious to carry out the optimization in
this way, without first checking for some pretty good packings that set a
threshold to worry about. But it could be done.
By contrast, seeking the TRUE minimal radius means allowing the cards
to be in arbitrary orientation, which adds 52 rotation variables and is
likely to be terribly inefficient. Even if those rotations are limited
to multiples of 90 degrees, you face a terrible combinatorial problem,
thinking about all possible ways to tile a portion of the plane with
these rectangles, each allowed independently to be vertical or
horizontal. (It may be a good first problem to figure out the smallest
disk that contains 52x35=1820 unit squares parallel to the axes, and then
look to partition them into 52 rectangles.)
Of course you will need a radius of at least sqrt(1820/pi), which is
about 24.1 . In the other direction, a radius of about 26.58 is enough:
place all the cards horizontally, in stacks of heights 4,8,9,10,9,8,4
cards (i.e. using no v's and using 7 h's, namely h1 = -24.5, h2=-17.5,
h3=-10.5, h4=-3.5, h5=3.5, h6=10.5, and h7=17.5.). This is less than the
answer given by Mr. Sengupta.
I'm stuck in a hotel room tonight so maybe I'll experiment with some
other combinations, but it's clear you're just going to get small
improvements in the interval [24.1, 26.6] and probably only after
lots of work!
This forum is accessible from China by the way.
|
| « Last Edit: Nov 17th, 2006, 9:13am by Michael Dagg » |
IP Logged |
Regards,
Michael Dagg
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #6 on: Nov 17th, 2006, 1:35pm » |
Quote Modify
|
Actually I take bake my answer. I only did half calculation. Here is what I did.
let's start with the simplest arrangement. Square.
Let's say we need x cars horizonal on 5 lenght side and y on 7 length side.
So total area is (5x)(7y) -> 52*5*7 --(1)
Now consider a circle of radius r, Let's compute the side of the largest square it can hold. It will be sqrt(2)*r. The area would be hence 2r^2.
Let's equate this to 2r^2 = 52*5*7 giving r=30.166 the answer i posted. I forgot to do next steps.
Let's comput sqrt(2)*r=42.66
This shows us the nearest integer side can be 42 in case of 7 length and 40 for 5 length.
Thus putting this in 1 we get x=8 and y = 6
i.e. we need 8 cards in length of 5 and 6 in length of 7 to form an approx square.
This gives us 48 cards. Now if we examine the empty space outside square inside circle we have plenty of space to put the remaining 4 cards.
Now let's compute the actual radius.
One side is 40 and other is 42. using pythagoras gives the diameter as 58 or radius as 29, which is even smaller than my previous answer or one given by Mr. Sengupta and very close to Icarus's lower bound.
|
|
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #7 on: Nov 17th, 2006, 8:09pm » |
Quote Modify
|
on Nov 17th, 2006, 9:03am, Michael_Dagg wrote:Of course you will need a radius of at least sqrt(1820/pi), which is
about 24.1 . |
|
Hmmm. Apparently, I can't use a calculator right, since I came up with 28.58 for this same calculation. 
on Nov 17th, 2006, 1:35pm, Sameer wrote:| 29, which is even smaller than my previous answer or one given by Mr. Sengupta and very close to Icarus's lower bound. |
|
Too close I thought, until I noticed that Michael_Dagg arrived at a smaller bound by the same calculation.
I have no idea how I came up with that number.
|
| « Last Edit: Nov 17th, 2006, 8:12pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #8 on: Nov 17th, 2006, 9:57pm » |
Quote Modify
|
on Nov 17th, 2006, 8:09pm, Icarus wrote:
Too close I thought, until I noticed that Michael_Dagg arrived at a smaller bound by the same calculation.
I have no idea how I came up with that number. |
|
Hmm and Apparently I can't read!!
But do you guys see any problem with my calculations?
|
|
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
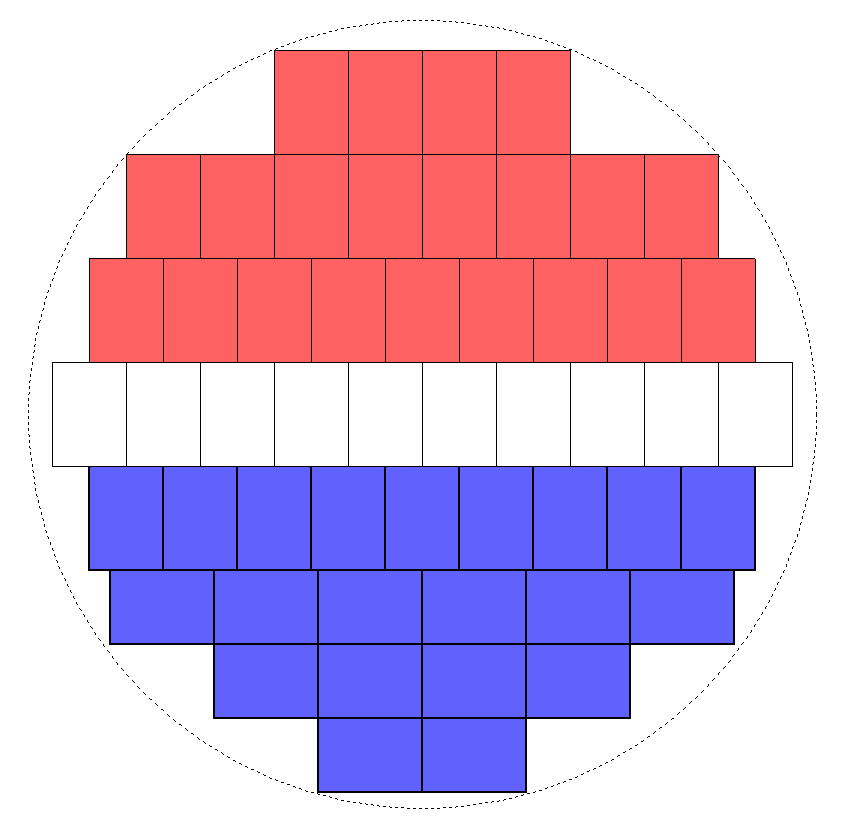
Michael's configuration (red) may be slightly improved as shown (blue). The difference is so small (26.433 vs 26.575) it's not seen on the drawing.
Exactly as Michael predicted.
I somehow believe that in the optimal solution all cards will have parallel edges.
|
|
IP Logged |
|
|
|
Sameer
Uberpuzzler
Pie = pi * e
Gender:
Posts: 1261
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #10 on: Nov 21st, 2006, 12:02pm » |
Quote Modify
|
I was imagining this shape (it was pretty obvious). It's like integrating over a circle. The best method I could think up was starting with a square like I shown. Then we can show that we have enought fit more cards within the empty space, thus leaving room even minimize the circle some more, and follow this iterative process. Can someone write a program to come up with the optimal arrangmenet?
|
|
IP Logged |
"Obvious" is the most dangerous word in mathematics.
--Bell, Eric Temple
Proof is an idol before which the mathematician tortures himself.
Sir Arthur Eddington, quoted in Bridges to Infinity
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #11 on: Nov 21st, 2006, 12:02pm » |
Quote Modify
|
I have an idea, i have not been able to work it out completely yet though.
I was trying to compute smallest circle for single card, two cards, three cards etc... (upto a certain n cards, n not very large).
Then among these find k-card configuration which has the smallest remainder area. Lets say that the k-card configuration gets inscribed in a circle of radius r'. Then find the smallest circle that can fit (52/k) circles of radius r'.
i was looking at this as an approximation that might work. My computational skills are a bit shoddy though. I havent finished computing things yet. Just thought, i would let everyone know about this.
-- AI
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
Ken_Wiley
Newbie
Gender:
Posts: 22
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #12 on: Nov 23rd, 2006, 10:25am » |
Quote Modify
|
on Nov 21st, 2006, 9:39am, Barukh wrote:| The difference is so small (26.433 vs 26.575) it's not seen on the drawing. |
|
I can get the radius 26.575 but not 26.433. How do get it?
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #13 on: Nov 24th, 2006, 1:04am » |
Quote Modify
|
on Nov 23rd, 2006, 10:25am, Ken_Wiley wrote:
I can get the radius 26.575 but not 26.433. How do get it? |
|
Look at the white-blue configuration in the drawing. Calculating the circle enclosing the cards layer by layer, we get:
White layer (10 cards): R = sqrt(252 + (7/2)2) = 25.244
Blue vertical layer (9 cards): R = sqrt((45/2)2 + (21/2)2) = 24.829
Blue horizontal layer (6 cards): R = sqrt(212 + (31/2)2) = 26.1
Blue horizontal layer (4 cards): R = sqrt(142 + (41/2)2) = 24.824
Blue horizontal layer (2 cards): R = sqrt(72 + (51/2)2) = 26.443
|
|
IP Logged |
|
|
|
Margit
Junior Member
Gender: 
Posts: 54
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #14 on: Nov 24th, 2006, 5:39am » |
Quote Modify
|
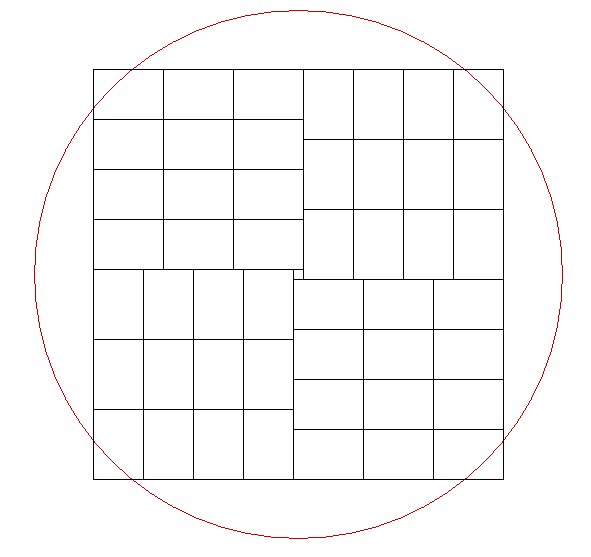
Does this approach bring anything ? -
Arrange 12 cards to give a rectangle of
21 x 20. Arrange 4 of these rectangles into a
41 x 41 square leaving a 1 x 1 hole in the middle.
Remove 1 (or more) cards from the corners and distribute lengthways with the remaining 4 cards along the sides.
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #15 on: Nov 24th, 2006, 7:53pm » |
Quote Modify
|
on Nov 21st, 2006, 9:39am, Barukh wrote:| I somehow believe that in the optimal solution all cards will have parallel edges. |
|
I agree.
Your improvement of 145/1000 might in fact be the only
such improvement possible.
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
on Nov 24th, 2006, 5:39am, Margit wrote:| Does this approach bring anything ? - |
|
Nice idea! However, I am afraid there is no room to distrubute the cards along the lines. I attached a drawing of your method below. The red circle is the "current best".
|
|
IP Logged |
|
|
|
Margit
Junior Member
Gender:
Posts: 54
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #17 on: Nov 26th, 2006, 2:06am » |
Quote Modify
|
Not giving up yet!
Remove the corner cards.
Go to bottom right corner -
Rotate the card above the now removed corner card by 90 degrees.
Go to bottom left corner -
Rotate the card to the right of the now removed corner card by 90 degrees.
Pull the circle in a NW direction to fit the bottom/right sides.
Does this bring anything ?
Packing squares in circles has some interesting results -
http://www.stetson.edu/~efriedma/squincir
|
| « Last Edit: Nov 26th, 2006, 2:22am by Margit » |
IP Logged |
|
|
|
Rompi
Newbie
Gender:
Posts: 2
|
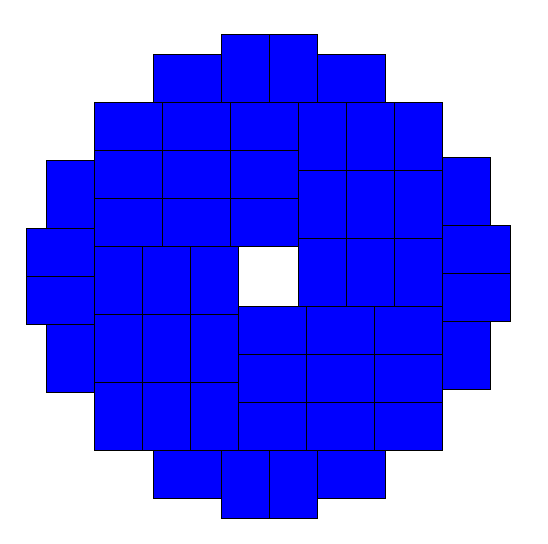
I found a nice solution with a radius of 25.94. The beauty of this arrangement is the overall high symmetry, look here:
|
|
IP Logged |
 |
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #19 on: Nov 26th, 2006, 9:15pm » |
Quote Modify
|
on Nov 26th, 2006, 3:19pm, Rompi wrote:| I found a nice solution with a radius of 25.94. The beauty of this arrangement is the overall high symmetry, look here: |
|
Wow!! 
The central part is similar to margit's solution, however a single row has been removed and rearranged at the exterior quite nicely.
-- AI
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #20 on: Nov 27th, 2006, 12:14am » |
Quote Modify
|
That's brilliant, Rompi! 
It is further amazing that this soluiton has a 6x6 hole in the middle! Is it possible to somehow use this space in order to get even more optimal configuration? 
|
| « Last Edit: Nov 27th, 2006, 12:16am by Barukh » |
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #22 on: Dec 14th, 2006, 9:13pm » |
Quote Modify
|
That's pretty good -- blows my result.
Why doesn't it surprise me that it's an annulus.
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
Mariko79
Newbie
Better than Van Damme
Posts: 30
|
|
Re: A Non-overlapping Circle Puzzle
« Reply #23 on: Apr 24th, 2013, 10:10am » |
Quote Modify
|
on Nov 24th, 2006, 5:39am, Margit wrote:Does this approach bring anything ? -
Arrange 12 cards to give a rectangle of
21 x 20. Arrange 4 of these rectangles into a
41 x 41 square leaving a 1 x 1 hole in the middle.
Remove 1 (or more) cards from the corners and distribute lengthways with the remaining 4 cards along the sides.
, |
|
Seems logical to me... ;)
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print