Author |
Topic: rope around the earth riddle (Read 14191 times) |
|
chinkygogo
Newbie
Gender: 
Posts: 4
|
 |
rope around the earth riddle
« on: Aug 18th, 2006, 3:37am » |
 Quote  Modify
|
Sorry i couldn't find the answer in the threads:
Assume the Earth is a perfect sphere of radius r and suppose a rope of zero elasticity is tied tightly around it. One metre is now added to the rope's length. If the rope is now pulled at one point as high as possible above the Earth's surface, what height will be reached?
I have been given an answer of 1m, though i think it is 0.5m as you have a slack of 1m left over and then you fold this in half to get the greatest distance from the surface or is there some deeply complex optimisation formula which gives a very silly answer of 1?
Cheers
|
|
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: rope around the earth riddle
« Reply #1 on: Aug 18th, 2006, 4:04am » |
Quote Modify
|
I'm fairly sure both answers are wrong.
Try it like this. Assume the earth is a perfect cube with sides X, and you have a rope with length 4X+1 tied around it, how far can you hold up the rope.
You're on one face of the earth, so 3X of rope won't budge. By pythagoras, you can reach a height of 1/2 sqrt((X+1)^2 -X^2) = 1/2 sqrt(2X+1), which is significantly more than 1 for most values of X
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
chinkygogo
Newbie
Gender:
Posts: 4
|
|
Re: rope around the earth riddle
« Reply #2 on: Aug 18th, 2006, 4:56am » |
Quote Modify
|
So would you assume some deeply complex optimisation formula considering that we are dealing with a circle that the triangle can be formed on top of and therefore the base of this triangle could start from anypoint along the upper hemisphere? or are you saying that the forumla is very easy as it is for the cube example i think i would disagree....although i am very happy to be proved wrong! 
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: rope around the earth riddle
« Reply #3 on: Aug 18th, 2006, 6:55am » |
Quote Modify
|
Looking at the diagram below, we see that where the original length of the rope was 2[pi]r, the new length of the rope is 2([pi] - [alpha])r + 2d. Therefore the difference is 2d - 2[alpha]r = 2d - 2r tan-1(d/r).
Since we know this difference is 1 (working in meters), we have 2d - 2r tan-1(d/r) = 1 --> tan-1(d/r) = d/r - 1/(2r). Setting r = 6378135 and solving numerically gives d ~ 39369.8.
Now, since d2 + r2 = (r+h)2, solving for h is straightforward: d2 + r2 = r2 + 2rh + h2 --> h2 + 2rh - d2 = 0 --> h = sqrt(r2 + d2) - r --> h = 121.5 meters, or roughly the height of a 40-story building!
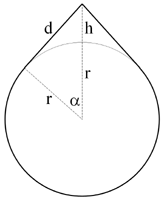
--SMQ
|
| « Last Edit: Aug 31st, 2006, 6:48am by SMQ » |
IP Logged |
--SMQ
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: rope around the earth riddle
« Reply #4 on: Aug 19th, 2006, 9:30am » |
Quote Modify
|
hmm.. that's a bit different that the number I got, but I might have to check it. (I also used a taylor approximation of tan)
There's a puzzle somewhere on the board that uses the moon instead of the earth, but in the same situation. If memory serves me it gave a larger answer there (at thus it should be much larger here too). But then, when has memory ever served me in the past..
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: rope around the earth riddle
« Reply #6 on: Aug 20th, 2006, 6:53am » |
Quote Modify
|
Note to self, don't use kilometer units for the radius, and meter units for the added rope length..
So using tan([alpha]) = [alpha] + 1/3[alpha]3 + O([alpha]5)
We can get
[alpha]3=3/(2*r) (using that [alpha] will be sufficiently small to ignore the O([alpha]5) error)
h = (1/cos([alpha]) - 1) * r
Which also gives 121.5 m
|
| « Last Edit: Aug 20th, 2006, 6:54am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
chinkygogo
Newbie
Gender:
Posts: 4
|
|
Re: rope around the earth riddle
« Reply #7 on: Aug 23rd, 2006, 6:01am » |
Quote Modify
|
Wow, whatever the answer is, it seems complex. Which is all I need to know really...if i can be bothered i may try to follow the maths, but I really wanted to find out whether there was an instinctive "easy" rationale, like the one i was given - "you add 1m, so therefore thats as much as you can lift". If the answer is 1m then I don't feel as though this 'easy' rationale would suffice. If the answer is 0.5m (as this is certainly 'one' of the heights that can be reached) then there needs to be a laymans rationale to dismiss more complex maths (i.e. higher than basic GSCE!) for this to be classed as a riddle! otherwise this should be classed as a good maths problem (not a riddle). Has anyone tried this practially with a tennis ball and a bit of string? With regards to your answers, (100m +) can anyone give a laymans explanation as to why giving minimal slack produces exponentiall growth in optimum height? (I haven't done any maths yet and may understand a bit more about this and stop relying on instinct by tomorrow). Thanks ever so much though, I will give it some more thought
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: rope around the earth riddle
« Reply #8 on: Aug 23rd, 2006, 7:25am » |
Quote Modify
|
chinkygogo, note that SMQ's diagram is not to scale.
h = sqrt(r2 + d2) - r
Expanding using the Binomial Theorem we get
h ~ d2/2r (as d/r is very small)
~ 121.5m
d2/2r = (d/r)(d/2)
We know that d/r is small.
So d is large.
Therefore h is much larger than 1 because d is large and d/r is small.
I hope this helps.
|
| « Last Edit: Aug 23rd, 2006, 10:08am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: rope around the earth riddle
« Reply #9 on: Aug 23rd, 2006, 7:38am » |
Quote Modify
|
on Aug 23rd, 2006, 6:01am, chinkygogo wrote:| With regards to your answers, (100m +) can anyone give a laymans explanation as to why giving minimal slack produces exponentiall growth in optimum height? |
|
It's not exponential, if you look at http://www.qbyte.org/puzzles/p004s.html there's a table at the end which shows how the height you can reach changes with the lengthening of the robe.
A small excerpt:
0.001m: h=1.2164405
0.01m: h=5.6462177
0.1m: h=26.207446
1m: h=121.64473
To get 100 times as high, you need to add 1000 times as much rope.
(However the relation gets more linear as you add more rope. Because the earth will seem more like a pinprick by comparison)
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: rope around the earth riddle
« Reply #10 on: Aug 23rd, 2006, 7:49am » |
Quote Modify
|
on Aug 23rd, 2006, 6:01am, chinkygogo wrote:| can anyone give a laymans explanation as to why giving minimal slack produces exponentiall growth in optimum height? |
|
Sure, try this experiment: grab a piece of string in both hands, about 8" (20cm) apart. Now use one of your thumbs to push the middle of the string down about 1" (2cm). Notice how your hands are only pulled together a little bit -- much less than 1"? Now move your hands 1" closer together and see how much you can move the string with your thumb now. More than 2", right?
The reason for it has to do with triangles and the pythagorean theorem, but it's easy to see that the amount you can move the middle of the string is more than the amount of slack, and the closer the string is to being straight, the greater the difference is.
Since a string around the Earth is very close to being straight, the difference between how much you can move the middle and the amount if slack is very large.
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
Fifis
Newbie
—Poet, composer, pianist.—
Gender:
Posts: 3
|
|
Re: rope around the earth riddle
« Reply #11 on: Aug 18th, 2013, 6:14pm » |
Quote Modify
|
Seems like it’s time to revive this little beauty in 2013! A complete solution with formulæ:
We have a circle of radius r and a point that is separated by h meters from it... on the outside. Two tangents and the bigger arc make up 2*Pi*r+a where a is our addition to the length of the rope. h=?
Please excuse my poor explanation since English is not my first language. The full central angle... Is it OK if I write in LaTeX syntax? You are supposed to interpret that and render it in your mind simultaneously, otherwise you wouldn’t be reading this forum, right? So, the full central angle between the two radii to the tangent points is \( \pi-2\alpha \), so the length of the arc is \( 2\pi r\frac{\pi + 2\alpha}{2\pi} = 2\pi r \left( \frac{1}{2}+\frac{\alpha}{\pi}\right) = \pi r + 2\alpha r \). Then
\[ 2\pi r + a = \left( \frac12 + \frac{\alpha}{\pi} \right) 2\pi r + 2b. \]
Consider \(\triangle ACD\). According to the law of sines, \( \frac{r}{\sin\alpha} = \frac{b}{\sin (\pi/2-\alpha)} = \frac{b}{\cos \alpha} = r + h \) (0<\alpha>\pi/2). Hence
\[ b = r \frac{\cos \alpha}{\sin \alpha} = r \cot \alpha. \]
Next, according to Pythagorean theorem, \( (r+h)^2 = r^2 + b^2 = r^2 + r^2 \cot^2 \alpha \). Then \( r^2 + 2rh + h^2 = r^2 + r^2 \cot^2 \alpha \), which yields \( \cot \alpha = \sqrt{\frac{2rh + h^2}{r^2}}\) and
\[ \alpha = \arccot \sqrt{\frac{2rh + h^2}{r^2}}. \]
Everything is positive, \alpha<\pi/2, therefore the omission of implied constraints and freedom with square roots.
Let’s replace b and \alpha in the initial equation:
\[ 2\pi r + a = \left( \frac12 + \frac{\alpha}{\pi} \right) 2\pi r + 2b, \]
\[ 2\pi r + a = \left( \frac12 + \frac{\mathop{\mathrm{arcctg}}\sqrt{\frac{2rh + h^2}{r^2}}}{\pi} \right) 2\pi r + 2r\sqrt{\frac{2rh + h^2}{r^2}}, \]
\[ \left( \frac12 - \frac{\mathop{\mathrm{arcctg}}\sqrt{\frac{2rh + h^2}{r^2}}}{\pi} \right) 2\pi r + a = 2\sqrt{2rh + h^2}, \]
\[ \pi r - 2 r \arccot \sqrt{\frac{2rh + h^2}{r^2}} + a = 2\sqrt{2rh + h^2}. \]
It’s the end. We cannot solve this monster for h analytically, for even such simple stuff like \( \arccot x - x = c \) cannot be explicitly written in terms of inverse functions. So let’s go for Wolfram Alpha, yay!
Code:| Solve Pi*6378137 - 2*6378137*arccot(\sqrt((h^2 + 2*6378137*h)/(6378137^2))) + 1= 2\sqrt(h^2 + 2*6378137*h) for h>0 |
|
The answer is 121.506 m! (I used the equatorial radius, which is slightly larger than average Earth radius).
For smaller amounts of rope added, the answer is even more drastic! For 1 foot (0.3048 m) the height added is 55 m, and even for 1 inch (0.0254 m) the height increase is 10.5 m! A single centimeter of rope added, 1 cm corresponds to 5.6 m! Maybe William Wu should add the following options: 1 foot is added... 1 inch is added... 1 cm is added... Let the counter-intuitive answers blow the minds of everybody!
|
| « Last Edit: Aug 18th, 2013, 6:15pm by Fifis » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print