 Author
Author |
Topic: TWO GAMBLING MACHINES (Read 2556 times) |
|
casual_kumar
Newbie


Gender: 
Posts: 21
|
 |
TWO GAMBLING MACHINES
« on: Aug 8th, 2006, 3:19am » |
 Quote Quote  Modify Modify
|
Computing average case of these equally likely events
(0.7 + 0.8 + 0.9 + 1.1 + 1.2 + 1.5)/6 = 1.03333
So, putting $1 in the machine will give $1.03333 on an average, in one play.
Answer to 1st question is YES, we can win. Odds of winning may be 50% in a single play (as 3 out 6 outputs are greater) but if we play for a long time, we will win on the average and hence 2nd way of playing is good.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: TWO GAMBLING MACHINES
« Reply #1 on: Aug 8th, 2006, 4:04am » |
 Quote Quote  Modify Modify
|
With the second method in the long run, you'd get each factor an equal number of times, and if you multiply them all, you get less than 1.
So you might want to check your motivation for choosing method 2 (you could also take a look at the earlier thread)
|
| « Last Edit: Aug 8th, 2006, 4:21am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Product
Newbie


x * y
Posts: 10
|
 |
Re: TWO GAMBLING MACHINES
« Reply #2 on: May 11th, 2007, 8:57am » |
 Quote Quote  Modify Modify
|
I hate to bring this thread back from its year long sleep, but the answer towr left is troubling me. I read through the earlier thread, which seems to indicate that method 2 is better, so I'm confused as to why in this thread the final answer is that #1 is better.
First off he says "and if you multiply them all, you get less than 1"
But that's not how to calculate the EV. As was stated in the previous thread, the EV calculation for each throw would be (.7x + .8x + .9x + 1.1x + 1.2x + 1.5x)/6.
I think the consideration for method one being better is that you are assuming an unlimited bankroll vs just $1 from method 2. This is flawed though because you cannot go bust if the worst you can get is .7x back. Expected value of the machine is positive, so on average each time you put money into the machine, you get back more than you put in. Since you are (in the long run) getting back more than you put in, with method two you are continually putting in MORE than just a dollar, specifically you are putting in 1.03x the previous bet, which started at a dollar. If you're getting #1 as better, I think that some math is wrong somewhere. I don't understand how a machine that yields a player's advantage could possibly put out LESS money by putting MORE money into it.
I'm not a math wiz, and I freely admit that some of the math flying around this place confuses me, but I am a gambler and I know that over an infinite amount of play, I will get back 1.03 times what I put in for every play. If I play 1x the previous bet in method one, and 1.03x my previous bet in #2, #2 will give a better result in the long run.
In the previoust thread, James Fingas says:
"Simulation is not well-suited to this problem. The vast majority of the time, your simulated results will be significantly less, but a small fraction of the time they will be spectacularly more."
Simulation is suited to every probability problem perfectly, but the numbers need to be huge. Somewhere around a billion would yield accurate results.
He also says:
"Keep in mind, however, that the game is linear: the amount of money you expect to win is based solely on the amount you put in the machine. "
Method 1 is linear. I am always putting in $1, I am always winning 1.03, since that's my EV.
Method 2 is exponential. I am betting my $1, then I am betting 1.03^1, then 1.03^2, then 1.03^3 and so on.
On the thousandth play of method 1, I am betting $1 and winning 1.03. So my profit is 1000 x .03, or 30.
On the thousandth play of method 2, I am betting 1.03^1000, and am winning 1.03^1001, and that's hundreds of billions of dollars.
I could very well be mistaken somewhere, but it seems to me that method 2 is clearly better. Some people have said that somehow method 2 is -EV, which just isn't possible. EV does not change based on bet size or betting pattern.
I hope this post doesn't come across as demeaning or undermining (especially since some of it may be incorrect.) I'm a substitute elementary teacher and solving these riddles is what I do while the kids are off somewhere else. So I have a lot of time to put my thoughts together, I'm not trying to be a jerk.
|
| « Last Edit: May 11th, 2007, 12:14pm by Product » |
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: TWO GAMBLING MACHINES
« Reply #3 on: May 11th, 2007, 6:31pm » |
 Quote Quote  Modify Modify
|
Let's try a simpler scenario:
The machine has 2 possible outcomes, each equally likely: For X dollars put in, it will return either 1.9X dollars or 0.2X dollars.
For each dollar put in, you can expect to get 1.05 dollars back. However, if you have an equal number of 0.2 results as 1.9 results (as is expected), then method #2 leaves you a return of (0.38)N/2 on your dollar after N pulls.
Even though according to William's and your analysis, Method 2 should pay-off even better for this machine than the original problem, in over 100,000 trials of 250 pulls, the WORST result I came up with for method 1 is about $200/$250 = 0.80, the BEST result I found for Method 2 was about 10-17.
In order for Method 2 to break even, you need to get 1.9 more than twice as often as 0.2. This is such an extremely rare occurrence, I wouldn't bother to hope for it! In fact, the more pulls you do in a run, the less likely it is that you will come out ahead
|
| « Last Edit: May 11th, 2007, 6:42pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Product
Newbie


x * y
Posts: 10
|
 |
Re: TWO GAMBLING MACHINES
« Reply #4 on: May 11th, 2007, 9:31pm » |
 Quote Quote  Modify Modify
|
--Please read the bottom before you read the body--
I think you have your expected value math confused, and don't understand how you could explain the results of betting one way vs. another generating different outcomes. Regardless of the bet, the EV is always the same. I'd also like to see how you programmed your trials, and I'd recommend doing WAY more pulls than 250 for any serious EV simulations. 250 is an irrelevant sample size for any gambling simulation, somewhere around 1,000,000 is better.
You say the return of (.2*1.9)N/2 is the EV, but I don't see how that's true. That means I'm losing a TON of money on every bet, which is impossible since I'm very very +EV. The EV calculation should be:
(.2x + 1.9x)/2 = 1.05 I recieve 1.05x my bet for every play.
You say you need twice as many 1.9s to break even, but that's not true. You say that you'd get almost exactly the same, and that is true. Here's what happens, assuming play of $1 per bet.
1,000,000 plays
.2 - 500,000 hits. Cost: 400,000 Return: 100,000
1.9 - 500,000 hits. Cost: 500,000 Return: 950,000
Total Cost: 1,000,000
Total Return: 1,050,000
50,000 is exactly what we though we'd make. So we are making 1.05 on each play. If we assume that method 1 is betting $1 flat, and method 2 is starting with $1 and always betting everything:
Method 1: Total number of plays * 1.05 is my return.
Method 2: 1.05plays
Method two is exponentially larger, to the point of being ridiculous.
-Final thoughts-
Okay I don't want to erase what I wrote, just for thought process purposes, but thinking more I do have method 2 wrong. In method one, you have a bankroll proportionate to the number of plays you make. Method two gives you a bankroll of only $1. The problem is not in the machine or the EV, but in risk of ruin. It is still true that I get 1.05x my previous bet, BUT I failed to consider that the size of my bet shrunk with every .2 hit. I think a better way to explain your theory would have been to say that you either get 2.1x or lose your bet. This is obviously insanely +EV, but since you lose your betting ability when you hit the 50/50 shot of losing your bet, it is useless.
You guys are too smart. 
|
| « Last Edit: May 11th, 2007, 10:12pm by Product » |
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: TWO GAMBLING MACHINES
« Reply #5 on: May 11th, 2007, 10:11pm » |
 Quote Quote  Modify Modify
|
on May 11th, 2007, 6:31pm, Icarus wrote:| In order for Method 2 to break even, you need to get 1.9 more than twice as often as 0.2. This is such an extremely rare occurrence, I wouldn't bother to hope for it! In fact, the more pulls you do in a run, the less likely it is that you will come out ahead |
|
Exactly. For those values, the probability of coming out ahead is around
1/ {2 {2 } }  c c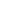 e-t^2/2dt ~ 5*10-12, e-t^2/2dt ~ 5*10-12,
where c =  {n}(r-1)/(r+1) = 6.8, r = -log1.9(.2) = 2.5. {n}(r-1)/(r+1) = 6.8, r = -log1.9(.2) = 2.5.
So it never happens in your simulation with << 1011 trials!
For two values a,b, and n pulls, the expected value of method 2 is
 k=0n C(n,k)/2n akbn-k = [(a+b)/2]n. k=0n C(n,k)/2n akbn-k = [(a+b)/2]n.
|
| « Last Edit: May 11th, 2007, 10:12pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: TWO GAMBLING MACHINES
« Reply #6 on: May 12th, 2007, 12:32am » |
 Quote Quote  Modify Modify
|
I know you changed your mind, but just for the record:
on May 11th, 2007, 9:31pm, Product wrote:| I think you have your expected value math confused, and don't understand how you could explain the results of betting one way vs. another generating different outcomes. |
|
I didn't calculate any expectations other than the trivial one for outcome of a single pull: 1.05
Quote:| Regardless of the bet, the EV is always the same. I'd also like to see how you programmed your trials, and I'd recommend doing WAY more pulls than 250 for any serious EV simulations. 250 is an irrelevant sample size for any gambling simulation, somewhere around 1,000,000 is better. |
|
I did 250 because I didn't program it. Instead I just set up a quick spreadsheet in Excel. Excel has a 256 column limit, so I stopped at 250 because it's a nice round number, and I'd have room for the statistics. Sum of trials gives the Method 1 return, Product gives the method 2 return. I filled 2000 rows representing separate trials and had it tell me the max product and minimum sum. Then I kept telling it to recalculate (which re-does all the random picks). I didn't bother to do any more because I knew it was unrealistic to try a sufficient number of trials with the resources I have at hand.
As for stopping the runs at 250, you are definitely mistaken if you think more pulls per run would improve matters. The higher the number of runs, the less likely it is that you are going to get the super majority of 1.9s that you need to break even. With only 5 or 10 pulls, you come out ahead on occasions. With 250, practically never. With 1,000,000 pulls, you could keep doing runs until the death of the universe and still never see a successful run. This is the law of large numbers in action.
Quote:| You say the return of (.2*1.9)N/2 is the EV, but I don't see how that's true. |
|
No I didn't say that. I said that in a run where the 0.2s and the 1.9s occur in equal numbers, 0.38N/2 is the value. I also pointed out that equal numbers of 0.2 and 1.9 is the expectation for these events - this is an obvious consequence of the two values being equally likely.
What came be deduced from those two facts is that 0.38N/2 is the median return for method 2. The expectation (or mean) is a different beast.
Quote:| You say you need twice as many 1.9s to break even, but that's not true. |
|
Yes it is. If in a method 2 run you've gotten K 1.9 values and L 0.2 values, then your outcome is $1*(1.9K)*(0.2L). This will be less than 1 unless K >= L(-log1.90.2) = (2.5075)L.
Quote:| You say that you'd get almost exactly the same, and that is true. |
|
?? what are you referring to here? I never said anything like this.
Quote:| Here's what happens, assuming play of $1 per bet. |
|
I.e. Method 1, which is not where the misunderstanding is. Everybody agrees on what happens under this method. In my trials, I was reporting the worst outcome I saw for method 1, which is why it was a loss instead of the expected win. The average outcome was much higher. Very close to 262.5/250 = 1.05, in fact.
Quote:method 2 is starting with $1 and always betting everything:
<snip>
Method 2: 1.05plays
Method two is exponentially larger, to the point of being ridiculous. |
|
Yet when you try this, it doesn't work. I am not exactly sure what is wrong with William's proof in the other thread. Probability theory has always been a weak point for me. My first thought was that even though trials where method 2 comes out ahead are extremely rare, they are also extremely lucrative - enough so that when they do occur, they balance out their rarity. But quite frankly, given Eigenray's calculation, the law of large numbers, and what I am seeing on the normal size of the shortfalls, it doesn't seem possible to me.
|
| « Last Edit: May 12th, 2007, 7:26am by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: TWO GAMBLING MACHINES
« Reply #7 on: May 12th, 2007, 8:52am » |
 Quote Quote  Modify Modify
|
For Icarus' version, method 2 does indeed give En=1.05n, but that's largely due to the large payout from the "jackpot" result.
For instance, applying method 2 with payouts of 0.04x and 5x each equally likely, the expected value per play is 2.52, with an expected payout over a run of 150 plays of 1.6*1060x, but the same run of 150 plays has only a 2.7*10-5 chance of not losing, over half of which is the chance of merely breaking even. Actually coming out ahead is 1.3*10-5 - or one run in almost 80,000, and over half of them leave you with only 5x for that game, while you will have lost most of 8*104x in the eighty thousand runs you played to get that one win... Or to put it another way, if you played one run per day for your entire life, you'd expect to win once, break even once, and lose more than 95% of your stake every single day of your life apart from those two, and for half the people that do this, their one win won't even pay for the week.
Your chances of getting the "jackpot" 7.0*10104x are 1 in 1.4*1045 but that singular event contributes almost a third of the expected value. The 150 runs where you only lose once contribute just over a third of the total expected value, and so on... By the time you get down to events that have a reasonable chance of occurring within the gambler's lifespan, the expected value is accounted for (and then some)
Of course, a good strategy is to play method 2 with relatively short runs, but lots of them - if you play 1024 runs of 10 games each, you will typically end up with around 107x, while playing 70 runs of 150 games each (roughly the same number of games) will typically leave you making a loss, and playing the same number of games using method 1 would leave you with around 26,000x
|
| « Last Edit: May 12th, 2007, 9:14am by rmsgrey » |
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: TWO GAMBLING MACHINES
« Reply #8 on: May 12th, 2007, 10:45am » |
 Quote Quote  Modify Modify
|
Which begs the question: If you are going to play the machine N = nk times, with n runs of k plays, for a fixed N, what values of n and k maximize your expected payout?
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: TWO GAMBLING MACHINES
« Reply #9 on: May 13th, 2007, 6:51am » |
 Quote Quote  Modify Modify
|
There's another strategy that looks intuitively appealing, though I'm not sure how it performs against the optimum nk strategy:
Reinvest your winnings every time you win, and start a new run every time you lose. That way, you win big on any significant winning streak, regardless of when it starts. The only slight drawback is that you only ever get a perfect run to end your session - every other run includes exactly one loss.
I suspect that whether this beats nk depends to some extent on R, the fraction of games you need to win to break even.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: TWO GAMBLING MACHINES
« Reply #10 on: May 13th, 2007, 8:44am » |
 Quote Quote  Modify Modify
|
on May 11th, 2007, 8:57am, Product wrote:| I hate to bring this thread back from its year long sleep, but the answer towr left is troubling me. I read through the earlier thread, which seems to indicate that method 2 is better, so I'm confused as to why in this thread the final answer is that #1 is better. |
|
Well, my answer wasn't so much to point out that method two was the wrong answer, as pointing out that the motivation needed more work.
The clever bit about the problem is that multiplying the factors gives a result less than 1, which might make you consider that it's worse. Explaining why, nevertheless, that isn't the case (at least not in terms of the expected gain) should be part of the solution.
|
| « Last Edit: May 13th, 2007, 9:08am by towr » |
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: TWO GAMBLING MACHINES
« Reply #11 on: May 13th, 2007, 9:06am » |
 Quote Quote  Modify Modify
|
on May 12th, 2007, 10:45am, Icarus wrote:| Which begs the question: If you are going to play the machine N = nk times, with n runs of k plays, for a fixed N, what values of n and k maximize your expected payout? |
|
The expected payoff is greatest with n=1 and k=N; however, getting that is the problem. With n=M and K=1 you minimize risk, but also have the least expected outcome.
You need to strike a balance between expected gain and variance (risk).
I suppose you could pick a criterium like "having 50% (or x%) chance of walking away with more than I brought in"; which is a reasonably human way to look at a decision problem like this.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: TWO GAMBLING MACHINES
« Reply #12 on: May 14th, 2007, 7:49am » |
 Quote Quote  Modify Modify
|
on May 13th, 2007, 9:06am, towr wrote:
The expected payoff is greatest with n=1 and k=N; however, getting that is the problem. With n=M and K=1 you minimize risk, but also have the least expected outcome.
You need to strike a balance between expected gain and variance (risk).
I suppose you could pick a criterium like "having 50% (or x%) chance of walking away with more than I brought in"; which is a reasonably human way to look at a decision problem like this. |
|
My instinct is to go for maximising your median payout - the value you have a 50% chance of doing at least as well as.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: TWO GAMBLING MACHINES
« Reply #13 on: May 14th, 2007, 10:59am » |
 Quote Quote  Modify Modify
|
on May 14th, 2007, 7:49am, rmsgrey wrote:| My instinct is to go for maximising your median payout - the value you have a 50% chance of doing at least as well as. |
|
I think you'd get the n=N and k=1 case again then. Because the median is where every factor occurs equally often. The distribution is terribly skewed; for larger k the median value goes down.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2873
|
 |
Re: TWO GAMBLING MACHINES
« Reply #14 on: May 15th, 2007, 10:58am » |
 Quote Quote  Modify Modify
|
on May 14th, 2007, 10:59am, towr wrote:
I think you'd get the n=N and k=1 case again then. Because the median is where every factor occurs equally often. The distribution is terribly skewed; for larger k the median value goes down. |
|
But, for N=10,000 games, say, having n=1, k=10,000 will indeed have a lousy median payout, and n=10,000, k=1 will have a modest payout, but what about the median for n=1,000, k=10? Just over 60% of the time, you'll have at least one "jackpot" run, so the median is going to be greater than the payout from a single jackpot run.
With n=5,000, k=2, the median is going to be close to 1250(a+b)2, while the median for n=10,000, k=1 is 5000(a+b)
For small k, the median total value over n runs is going to be n times the mean value or:
median = (N/k)*(((a+b)/2)k-1)
(the minus 1 is to account for the initial cost)
Obviously, this breaks down at large k, and I suspect the critical value is around N=k2k.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register