 Author
Author |
Topic: Measure out 10 ltrs using 13 and 7 ltrs ? (Read 1658 times) |
|
Subhobroto Sinha
Newbie



Gender: 
Posts: 3
|
 |
Measure out 10 ltrs using 13 and 7 ltrs ?
« on: Aug 13th, 2005, 11:52pm » |
 Quote Quote  Modify Modify
|
Hi mates
I tried looking for a similar thread, but found none, so here's a smart ass kinda puzzle :
You have 3 buckets : an empty 19 ltr, and two filled up buckets of capacity 13ltrs and 7 ltrs
Show how you will measure out 10 ltrs WITHOUT using any other container, except the 3 given..
I am not interested in the solution iteself, but rather the approach, so be verbose a little.. 
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #1 on: Aug 14th, 2005, 7:08am » |
 Quote Quote  Modify Modify
|
There is a beautiful approach using billiards.
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #2 on: Aug 14th, 2005, 6:59pm » |
 Quote Quote  Modify Modify
|
I'm not sure how billiards ties in to this, but riddles like this one are an application of the following theorem:
If the greatest common divisor of a finite set {ni} of integers is d, then there exist other integers {ai} such that a1n1 + a2n2 + a2x3 + ... = d.
In this case, 7 and 13 are relatively prime, so their greatest common divisor is 1. By the theorem, there are integers a, b such that a*7 + b*13 = 1. And in fact, it is easy to find that 2*7 + (-1)*13 = 1. Multiply through by 10, and we get 20*7 - 10*13 = 10.
This gives us one (highly inefficient) solution to the problem: we keep dumping the contents of the 7 liter bottle into the 19 liter one, refilling it from the 13 liter bottle, and refilling the thirteen liter bottle from the 19 liter one, as needed. After we have dumped the 7 liter bottle 20 times, and refilled the 13 liter bottle 10 times, 10 liters of water will remain in the 19 liter bottle.
The solution can be improved upon by finding a minimal pair a, b such that 7a + 13b = 10 (i.e.: 7*(7) - 13*(3)). It may be improved some more by making use of the 19 liter bottle to measure, not just serve as a holding container.
|
| « Last Edit: Aug 14th, 2005, 6:59pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sjoerd Job Postmus
Full Member
  

Posts: 228
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #3 on: Aug 15th, 2005, 2:42am » |
 Quote Quote  Modify Modify
|
Well, I'm wondering if the buckets are perfectly cilindrical.
If so, you could just tilt it in a fashion in which a line between the top-left and bottom-right is level.
Tilt the 13 and the 7 bucket in that fashion above the 19 bucket, seeing that it empties.
Otherwise?
Well... I don't know, I think Icarus is right
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ? 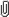 7_13_19.JPG 7_13_19.JPG
« Reply #4 on: Aug 15th, 2005, 11:02am » |
 Quote Quote  Modify Modify
|
on Aug 14th, 2005, 6:59pm, Icarus wrote:| I'm not sure how billiards ties in to this |
|
Here's how (see the attached drawing).
Consider a billiard in the form of a parallelogram with an angle 60o and sides ratio 13:7.
Draw two segments (red and cyan) perpendicular to the sides, as depicted - they will represent the capacities of 13 and 7 liters. Draw the third (green) segment to represent the 19 liters capacity, as in the picture.
Any state in the process is represented by the points on the boundary of the parallelogram. To translate this into the quantities of the buckets, just drop perpendiculars onto 3 colored segments, and read the fractions. In the picture, all the depicted points except one represent legal states (can you find the exception?).
We begin in the top-right corner, which corresponds to the initial state (13, 7, 0). The pouring process is the sequence of ball reflections in the "sides of the billiard" according to the usual "mirror reflection law". The first move is along the side of the parallelogram. Note that every section of the path is perpendicular to some colored segement, meaning that the corresponding bucket is not involved in the pouring.
The whole trajectory is the magenta path. It has 18 sections. Translating them into buckets' states, the solution starts as follows:
13 7 0
13 0 7
6 7 7
6 0 14
0 6 14
13 6 1
...
|
|
 IP Logged IP Logged |

|
|
|
River Phoenix
Junior Member
 

Gender: 
Posts: 125
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #5 on: Aug 15th, 2005, 12:48pm » |
 Quote Quote  Modify Modify
|
It is helpful to realize that we can simply throw away some of the water as we go, allowing us to isolate an odd ball amount of water in one bucket, and then empty the bucket into the ground - leaving room to continue.
Through a little bit of trial and error, with the numbers I was looking for in mind, and by quickly recognizing bad pathways, I came up with this solution:
0/19 13/13 7/7
7/19 13/13 0/7
7/19 6/13 7/7
14/19 6/13 0/7
19/19 1/13 0/7
12/19 1/13 7/7
12/19 8/13 0/7
5/19 8/13 7/7
5/19 13/13 2/7 ;isolated 2 units
5/19 13/13 0/7 ;dump 2 units
5/19 6/13 7/7
11/19 0/13 7/7
11/19 7/13 0/7
4/19 7/13 7/7
4/19 13/13 1/7 ;isolated 1 unit
4/19 13/13 0/7 ;dump 1 unit
0/19 13/13 4/7
0/19 10/13 7/7 ;WIN!
|
| « Last Edit: Aug 15th, 2005, 1:00pm by River Phoenix » |
 IP Logged IP Logged |
|
|
|
JocK
Uberpuzzler
    

Gender: 
Posts: 877
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #6 on: Aug 15th, 2005, 2:51pm » |
 Quote Quote  Modify Modify
|
on Aug 15th, 2005, 11:02am, Barukh wrote:
Here's how (see the attached drawing).
|
|
Wow..!! This is really beatiful Barukh..!
Did you invent this graphical representation yourself?
|
|
 IP Logged IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
RiverPhoenix
Guest

|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #7 on: Aug 15th, 2005, 3:09pm » |
 Quote Quote  Modify Modify
 Remove Remove
|
I just realized that my solution has the same number of steps as Barukh's (probably the same solution, then).
But my strategy was simply to realize that if we can get down to 17 units total, we are done. It is impossible to isolate 3 from the outset. It is possible to isolate 1 unit, but then after a while one will hit a dead end. Finally I tried isolating 2 units, which worked. Throwing out those 2 units, it was easy to isolate the last unit.
I guess this could be considered the "standard" approach. Barukh's method would be the "I am a rock star" approach
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #8 on: Aug 15th, 2005, 3:21pm » |
 Quote Quote  Modify Modify
|
on Aug 15th, 2005, 11:02am, Barukh wrote:| Here's how (see the attached drawing). |
|
Nice. You should make one change though: Instead of the parallelogram, you need to cut off the 0,0 corner back to the 19 liters-in-the-19-liter-bucket line, leaving you with a 5-sided figure, to truly represent the situation we have here. You can even represent RiverPhoenix's wasteful ways by allowing moving along the sides to the appropriate zero, as well as the reflection moves (it spoils the billiards analogy, but it still leaves a nice visual image).
RiverPhoenix: actually, your method has 17 steps compared to Barukh's 18. Note that each of your lines is a point on the graph, whereas a step is represented by the segment connecting the points.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
I was wrong about representing RiverPhoenix's method by movements towards zero. In fact, movement from a point in any of the three principle directions is possible without loss of water. The reflective moves represent completely filling or emptying the 7 or 13 liter buckets, while the non-reflective direction represents completely filling or emptying the 19 liter bucket.
Since emptying or filling the 19 liter bucket represents movement along the sides of the quasi-parallelogram, doing so will always leave you at one of its vertices.
With this in mind, I examined each of the vertices to see which was closest to one of the three victory points (expressed by (7-liter content, 13-liter content, 19-liter content), these are the points (7, 10, 3), (7, 3, 10), and (0, 10, 10)) using only 7-liter and 13-liter operations, and found that the corner (0,1,19) was closest (13 transfers away from (7,3,10)). Using a 19-liter transfer to get to this point gives the following path of length 15:
(7,13,0)
(0,13,7)
(0,1,19) (19-liter transfer)
(7,1,12)
(0,8,12)
(7,8,5)
(2,13,5)
(2,0,18)
(0,2,18)
(7,2,11)
(0,9,11)
(7,9,4)
(3,13,4)
(3,0,17)
(0,3,17)
(7,3,10)
Unless I've overlooked something (which never happens - honest!), this is the shortest non-wasteful path. Attached is a graphic representation I put together rather painstakingly using Word.
In order to examine the possibility of discarding water in this fashion, you would need to introduce a 3rd dimension to the graph. The third dimension would represent interactions in which water is placed in a "4th container". Since no such container actually exists, additional rules would be in place that deny the recovery of any water placed in this container.
|
| « Last Edit: Aug 15th, 2005, 7:49pm by Icarus » |
 IP Logged IP Logged |

"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
markr
Junior Member
 

Gender: 
Posts: 90
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #10 on: Aug 15th, 2005, 10:24pm » |
 Quote Quote  Modify Modify
|
on Aug 15th, 2005, 2:51pm, JocK wrote:
Wow..!! This is really beatiful Barukh..!
Did you invent this graphical representation yourself?
|
|
I saw this (without the three external lines) years ago in a book that I can't seem to find. I thought it was a Martin Gardner book, but no luck finding it.
edit: Eureka! I found it in my Applied Combinatorics text.
|
| « Last Edit: Aug 15th, 2005, 10:47pm by markr » |
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #11 on: Aug 16th, 2005, 6:19am » |
 Quote Quote  Modify Modify
|
on Aug 15th, 2005, 2:51pm, JocK wrote:Wow..!! This is really beatiful Barukh..!
Did you invent this graphical representation yourself? |
|
This approach is known for at least 65 years. I just adopted it for the specific problem at hand.
on Aug 15th, 2005, 3:21pm, Icarus wrote:| Nice. You should make one change though: Instead of the parallelogram, you need to cut off the 0,0 corner back to the 19 liters-in-the-19-liter-bucket line, leaving you with a 5-sided figure, to truly represent the situation we have here. |
|
That’s exactly what I meant when saying that exactly one point on the parallelogram is not reachable. The full parallelogram is obtained when the capacity of the bigger bucket is the sum of the capacities of small buckets (as, for instance, in 5-7-12 configuration).
With the new figure at hand, your nice solution is “almost classical mirror reflection”, except the first turn.
|
|
 IP Logged IP Logged |
|
|
|
SWF
Uberpuzzler
    

Posts: 879
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #12 on: Aug 16th, 2005, 10:41pm » |
 Quote Quote  Modify Modify
|
on Aug 15th, 2005, 10:24pm, markr wrote:
I saw this (without the three external lines) years ago in a book that I can't seem to find. I thought it was a Martin Gardner book, but no luck finding it. |
|
I think the bouncing ball approach is described in Martin Gardner's Sixth Book of Mathematical Games from Scientific American. I don't have that book, but I remember seeing this in a Gardner book from a particular small library and am pretty sure that is the only Gardner book this library had (shame on them).
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #13 on: Aug 17th, 2005, 12:22am » |
 Quote Quote  Modify Modify
|
on Aug 16th, 2005, 10:41pm, SWF wrote:| I think the bouncing ball approach is described in Martin Gardner's Sixth Book of Mathematical Games from Scientific American. |
|
It is also present in the 7th edition of Hugo Steinhaus's "Mathematical Snapshots" classic, published in 1954. It cites M. Tweedie's article in Mathematical Gazette from 1939.
|
|
 IP Logged IP Logged |
|
|
|
JocK
Uberpuzzler
    

Gender: 
Posts: 877
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #14 on: Aug 17th, 2005, 1:23pm » |
 Quote Quote  Modify Modify
|
on Aug 16th, 2005, 10:41pm, SWF wrote:
[..] Martin Gardner's Sixth Book of Mathematical Games from Scientific American. [..]
|
|
on Aug 17th, 2005, 12:22am, Barukh wrote:
[..] the 7th edition of Hugo Steinhaus's "Mathematical Snapshots" classic, published in 1954. [..]
|
|
It is like hijacking this thread, but guess that is no problem now that this riddle is so elegantly solved. So, would like to ask you all: what are the best recreational math books that you have read? I am particularly keen to hear about books that present novel and surprising insights. (Preferrably books that can be ordered on internet.)
|
|
 IP Logged IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Measure out 10 ltrs using 13 and 7 ltrs ?
« Reply #15 on: Aug 17th, 2005, 11:09pm » |
 Quote Quote  Modify Modify
|
on Aug 17th, 2005, 1:23pm, JocK wrote:| So, would like to ask you all: what are the best recreational math books that you have read? I am particularly keen to hear about books that present novel and surprising insights. (Preferrably books that can be ordered on internet.) |
|
Oh, that’s a tough question! You should put it in the hard section. 
Here’re some books that impressed me:
Ball & Coxeter, “Mathematical Recreations and Essays”
Littlewood's Miscellany
Conway & Guy. “The Book of Numbers”.
R. Courant and H. Robbins. “What is Mathematics?”
H.Dorrie “100 Great Problems Of Elementary Mathematics” (not exactly popular)
Hilbert & Cohn-Vossen. “Geometry and the Imagination” (JocK, I’m sure you would love that book!)
G.Polya. “How To Solve It” (Contains an account of how Euler computed the famous sum of reciprocals of integers’ squares)
R. Smullyan “Lady or the Tiger? And Other Logic Puzzles Including a Mathematical Novel That Features Godel's Great Discovery” (especially the Novel).
You may also want to look into Alex Bogomolny’s list.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register