Author |
Topic: Pythagorean dissection (Read 600 times) |
|
JocK
Uberpuzzler
Gender: 
Posts: 877
|
 |
Pythagorean dissection
« on: Feb 6th, 2005, 11:27am » |
 Quote  Modify
|
You have to teach a class Pythagoras' theorem. You decide to make a puzzle to help them understand this theorem.
Someone told you that one can dissect a square of area a2 into four equal pieces such that when a square of area b2 is added as a fifth piece, the five pieces together can be rearranged into a square of area a2+b2.
For arbitrary a > b, what is the shape of the four identical pieces that you have to construct?
|
| « Last Edit: Feb 6th, 2005, 11:59am by JocK » |
 IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
Note that this can be done as a pivot puzzle.
|
|
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
Well done Barukh.
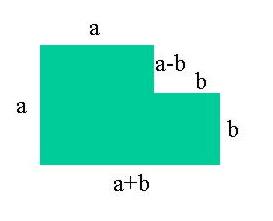
Perhaps an even better educational tool originates when dissecting below L-shape into 4 equal triangles and a square such that the five pieces can be put together in the form of a square.
What is the shape of the triangles, and what is the size of the square?
|
|
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print
Pythagorean_Dissection.zip