Author |
Topic: How Many Logic Functions (II) (Read 139484 times) |
|
Mike_V
Junior Member
Gender: 
Posts: 60
|
 |
How Many Logic Functions (II)
« on: Oct 3rd, 2003, 1:16am » |
 Quote  Modify
|
Hope you don't mind me expanding on your topic title (from the easy section).
So, you have a large number of possible logic functions with 5 boolean variables. How many of those function are essential? That is, how many functions are necessary so that using only those functions you can generate all possible functions?
Sorry if this is unclear. I'll give a 2 variable example.
Three (of the 16) functions with 2 boolean variables are:
a b|f 1 f2 f3
T T| T F F
T F| F T T
F T| F F T
F F| F T T
Here it is apparent that f3(a,b) = f2(f1(a,b),f1(a,b)). Thus you can generate f3 from the other two, so it is not necessary if you already have f1 and f2.
So, how many functions (and which ones) are essential in 5-variables? K-variables?
|
|
 IP Logged |
Don't specify the unspecified.
|
|
|
BNC
Uberpuzzler
Gender:
Posts: 1732
|
|
Re: How Many Logic Functions (II)
« Reply #1 on: Oct 3rd, 2003, 1:36am » |
Quote Modify
|
I beleive a single function is required for all K.
|
|
IP Logged |
How about supercalifragilisticexpialidociouspuzzler [Towr, 2007]
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: How Many Logic Functions (II)
« Reply #2 on: Oct 3rd, 2003, 2:31am » |
Quote Modify
|
I think BNC is right. You can make any arity function from one two-arity function, notably NAND or NOR, if I recall correctly..)
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: How Many Logic Functions (II)
« Reply #3 on: Oct 3rd, 2003, 11:32am » |
Quote Modify
|
Yes, 2-input NAND and 2-input NOR are universal, because you can make the functions AND, OR, and NOT using only NANDs (or NORs), and every Boolean function can be represented using ANDs, ORs, and NOTs. (The set of operators {AND, OR, NOT} is thus called functionally complete.) Thus if I recall correctly, most technology nowadays is built out of NAND gates.
Maybe someone will be inclined to prove that you can make AND, OR, and NOT out of NANDs -- actually that was an interview question I once saw nVidia give during a career fair. As for me I'm going to lunch.
|
| « Last Edit: Oct 3rd, 2003, 11:33am by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
BNC
Uberpuzzler
Gender:
Posts: 1732
|
|
Re: How Many Logic Functions (II)
« Reply #4 on: Oct 3rd, 2003, 3:14pm » |
Quote Modify
|
on Oct 3rd, 2003, 11:32am, william wu wrote:
Thus if I recall correctly, most technology nowadays is built out of <hidden> gates.
|
|
Not quite. Some years back, ASIC (application specific integrate circuit) technology had the "gate array" (GA) or "sea of gates" that where just many many NAND gates.
Today, the popular ASIC (term used in the wide sense) are (simplified):
- PAL (programmable array of logic) are basically "standard" complex function (actual function depends upon specific component), with selectable inputs.
- FPGA (field-programable GA) are RAM lookup table-based
- Standard cell devices have a library of common functions optimised at the silicon level
- Full custom devices work in the single transistor level.
Quote:
Maybe someone will be inclined to prove that you can make AND, OR, and NOT out of <hidden>
|
|
OK::
NOT(A) = NAND (A, A)
AND (A, B) = NOT( NAND (A, B))
and utilizing De-Morgan's rule:
OR(A,B) = NAND( NOT(A), NOT(B))
In he original question, to finish the "proof", we need to show that a two-input NAND (for example) may be obtained from a K-input NAND, but that's trivial by shortening (K-1) inputs togeter
The fact its possible to create K-input functions (K>2) from 2-input functions is actually by-definition in the case of primitive (basic) functions.
|
| « Last Edit: Oct 3rd, 2003, 3:21pm by BNC » |
IP Logged |
How about supercalifragilisticexpialidociouspuzzler [Towr, 2007]
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: How Many Logic Functions (II)
« Reply #5 on: Oct 4th, 2003, 11:01am » |
Quote Modify
|
on Oct 3rd, 2003, 11:32am, william wu wrote:| Thus if I recall correctly, most technology nowadays is built out of <hidden> gates. |
|
It's much too inefficient to do that, XOR for instance has a much, much more efficient implementation. Specialized subcircuits can safe a lot of time, energy in computation and space and connection-problems in chip-manufacturing.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
on Oct 4th, 2003, 11:01am, towr wrote:
It's much too inefficient to do that, XOR for instance has a much, much more efficient implementation. Specialized subcircuits can safe a lot of time, energy in computation and space and connection-problems in chip-manufacturing. |
|
The most efficient CMOS implementation of NAND I know of uses 4 transistors: 2 PMOS in parallel and 2 NMOS in series.
I've only seen XOR made from six CMOS transistors, but according to this google search result http://www.ap-asic.org/2000/proceedings/2-2.pdf there are 4 transistor implementations for single-rail inputs, which is the most efficient implementation as of the year 2000. (Which to me begs the question, why was it not until the year 2000 that someone figured out how to make XOR from 4 transistors with single-rail inputs? It seems like there's only so many ways to hook up a small number of transistors, I would've thought all the possibilities had been explored long ago -- if not by analytical methods, then by brute force. I'm not a circuits guy though, so maybe someone could explain to me why this is hard.) I couldn't find what the most efficient implementation is for double-rail.
The double-rail vs. single-rail distinction is new material to me, but if I understand it correctly, the NAND implementation with 4 CMOS transistors is also single-rail, since it doesn't assume that complements of the inputs exist. Thus the transistor count is 4 for both XOR and NAND, which makes me wonder how XOR can have a "much, much more efficient implementation". (Maybe in the double-rail comparisons for which I could find no information?)
Attachment: NAND in CMOS
|
| « Last Edit: Oct 6th, 2003, 4:01am by william wu » |
IP Logged |
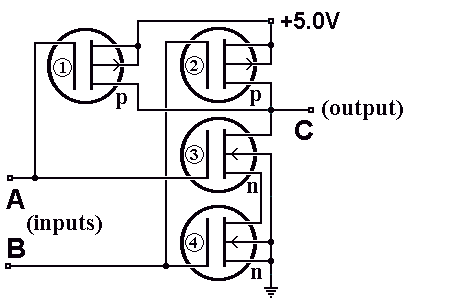
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: How Many Logic Functions (II)
« Reply #7 on: Oct 6th, 2003, 5:37am » |
Quote Modify
|
on Oct 6th, 2003, 1:39am, william wu wrote:
Thus the transistor count is 4 for both XOR and NAND, which makes me wonder how XOR can have a "much, much more efficient implementation". |
|
I think you misunderstood me.
Consider this, how many NANDS does it cost you to make a XOR ? Since it's more than one, it's more efficient to implement the XOR seperately, and not as a bunch of NANDs put together. The same goes for many other subcircuits.
Making subcircuits from NANDs makes them rather large quickly. And even though it has the benefit of only having to create the same simple gate over and over at different locations, it makes the circuits slower, and makes them use more energy.
I can't see you attachment btw. It shows up rather black.
|
| « Last Edit: Oct 6th, 2003, 5:43am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: How Many Logic Functions (II)
« Reply #8 on: Oct 9th, 2003, 5:31am » |
Quote Modify
|
OK, fair enough. I thought you were arguing that XOR + something else would be a better alternative for NAND in making a universal set, because somehow XOR uses less transistors than NAND. Repeating NAND over and over makes layout simpler, but is perhaps only acceptable in low-frequency designs.
|
|
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print