Author |
Topic: Global Traversal 2 (Read 4851 times) |
|
Kozo Morimoto
Junior Member
Posts: 114
|
 |
Global Traversal 2
« on: Jan 2nd, 2003, 3:15pm » |
 Quote  Modify
|
I saw this riddle in another forum, but I was unsatisfied with the answer, so I'll post it here in the hope that I can get a decent discussion.
You start at the equator and go north-east. How much distance do you cover when you get to the north pole? How many 'revs' around the pole would you do?
(Assume circumference is 40,000km [current estimate is 40,079km, so its close enough!] and that Earth is spherical and that you can travel over water etc.)
|
| « Last Edit: Oct 23rd, 2003, 8:11pm by Icarus » |
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender: 
Posts: 13730
|
|
Re: NEW: Global Traversal 2
« Reply #1 on: Jan 3rd, 2003, 1:10am » |
Quote Modify
|
It would, I think, take forever to reach the north pole.. But of course that doesn't mean the distance isn't finite..
I think this calls for an integral along a parametric line, and I forgot how to do that..
Although.. you walk as much east as north, so 10,000 km north, and 10,000 km east is about 14,142 km north-east..
But then, that would make the earth a cilinder, rather than a sphere..
|
| « Last Edit: Jan 3rd, 2003, 1:14am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
redPEPPER
Full Member
Posts: 160
|
|
Re: NEW: Global Traversal 2
« Reply #2 on: Jan 3rd, 2003, 4:35am » |
Quote Modify
|
on Jan 3rd, 2003, 1:10am, towr wrote:| It would, I think, take forever to reach the north pole.. But of course that doesn't mean the distance isn't finite.. |
|
If the distance is finite and you're moving at a constant speed, then it won't take forever.
But you will make an infinite number of revolutions around the pole. This is similar to the point I was trying to make with the beetle riddle. Maybe you can use it to solve this one. The fact that we're dealing with a sphere frightens me  If I work on a planar projection of the northern hemisphere like this one:
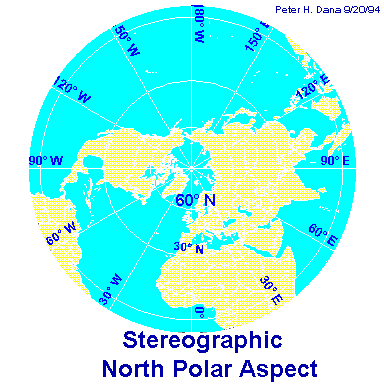
then the problem is the same as the beetle problem, and can be solved easily.
But the problem with this map (as with any planar map of a sphere) is distortion.
Too much math involved for me to take that into account. Maybe someone can take it from here.
Edit:
Quote:Although.. you walk as much east as north, so 10,000 km north, and 10,000 km east is about 14,142 km north-east..
But then, that would make the earth a cilinder, rather than a sphere.. |
|
Ohh, I missed that part. A nice, easy solution. Why do you think this wouldn't work for a sphere?
|
| « Last Edit: Jan 3rd, 2003, 4:42am by redPEPPER » |
IP Logged |
|
|
|
Kozo Morimoto
Junior Member
Posts: 114
|
|
Re: NEW: Global Traversal 2
« Reply #3 on: Jan 4th, 2003, 6:26pm » |
Quote Modify
|
The 'solution' I saw posted on another forum suggested straight trig 1/sqrt(2) m travelled for every 1m travelled north and east, but I'm not too convinced that this is the 'correct' assumption given a surface of a sphere. I wanted to see if someone can translate the NE travel into some kind of spherical coordinate system, which I tried to get my head around but couldn't.
|
|
IP Logged |
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: NEW: Global Traversal 2
« Reply #4 on: Jan 4th, 2003, 8:52pm » |
Quote Modify
|
That easy approach is correct, but if you want the equation in spherical coordinates here it is:
phi=ln( (1-cos(theta))/sin(theta) )
Here, I use phi as "longitude" and theta measured from the pole (pi/2 at the equator, 0 at north pole). The radius is held constant at R.
This gives d(phi)/d(theta) = 1/sin(theta)
In spherical coordinates an element of length is given by:
ds2= dr2 + r2*d(theta)2+ r2*sin2(theta)*d(phi)2
Arc length of the spiral is found by setting dr=0, replacing d(phi) using the expression above for d(phi)/d(theta) and integrating theta from pi/2 to 0: gives R*sqrt(2)*pi/2. It can be seen that d(phi) and the d(theta) terms are equal and the dr term is zero. Thus, at every instant the path bisects the angle between the latitude and longitude lines and moves northeast.
|
|
IP Logged |
|
|
|
Chronos
Full Member
Gender:
Posts: 288
|
|
Re: NEW: Global Traversal 2
« Reply #5 on: Jan 17th, 2003, 2:58pm » |
Quote Modify
|
An interesting side note, by the way: If you plot such a path (or indeed, any path of constant bearing) on a Mercator projection map, the path will be a straight line. This feature of the Mercator projection is why it's so valued among navigators, and also helps to show why the poles can never be shown on a Mercator map (most of the Merc maps you see in classrooms, textbooks, etc. cut off at about the arctic and antarctic circles).
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print