Author |
Topic: Bimagic Square Reconstruction (Read 1823 times) |
|
Barukh
Uberpuzzler
Gender: 
Posts: 2276
|
A bimagic square is a magic square that retains its properties after every element is squared.
That is: A bimagic square is a square matrix n x n with the following properties:
1. Every number 1, ..., n2 appears in the matrix.
2. The sum of numbers at every row, every column and two main diagonals is the same.
3. The sum of squares of numbers at every row, every column and two main diagonals is the same.
That bimagic squares exist is not immediately evident (at least for me). However, it was proved that they exist for every n > 7.
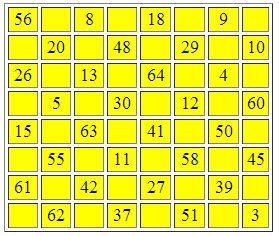
Now - the problem. You are given a partially populated bimagic square of order 8. Put in the missing numbers.
It is very probable that solution may be obtained - and quite quickly - by programming. The question is: how far can we go without any programming at all?
Note that this bimagic square was built 124 years ago!
|
| « Last Edit: Aug 9th, 2014, 7:22am by Barukh » |
 IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
 |
Re: Bimagic Square Reconstruction
« Reply #1 on: Aug 10th, 2014, 7:43am » |
 Quote  Modify
|
nitpick: two of the square's properties (1 and 3 in your list) are not retained when every element is squared...
|
|
IP Logged |
|
|
|
dudiobugtron
Uberpuzzler
Posts: 735
|
|
Re: Bimagic Square Reconstruction
« Reply #2 on: Aug 10th, 2014, 5:14pm » |
Quote Modify
|
on Aug 10th, 2014, 7:43am, rmsgrey wrote:| nitpick: two of the square's properties (1 and 3 in your list) are not retained when every element is squared... |
|
I took 'that is' to be an indicator that the properties listed were a more rigourous definition; a rewording of the earlier definition rather than a continuation.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print