Author |
Topic: Monotone Paths in Graphs (Read 8831 times) |
|
william wu
wu::riddles Administrator
Gender: 
Posts: 1291
|
 |
Monotone Paths in Graphs
« on: Nov 8th, 2011, 1:45pm » |
 Quote  Modify
|
Given an undirected connected graph with E edges, arbitrarily each edge with a unique number between 1 and E.
Show that there exists a path with monotone labels whose length is at least the average degree of the graph.
|
| « Last Edit: Nov 10th, 2011, 11:39am by william wu » |
 IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Monotone Paths in Graphs
« Reply #1 on: Nov 9th, 2011, 8:40am » |
Quote Modify
|
Your problem "hints" at a Ramsey theory solution using the Erdos result on increasing
or decreasing sequences of a certain length.
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Monotone Paths in Graphs
« Reply #2 on: Nov 10th, 2011, 6:58am » |
Quote Modify
|
Hm... I must be missing something.
Is the "average degree" the average number of edges that meet at a vertex?
By saying that the statement is true for a random placement of labels, do you mean it is true for all placements?
Because the way I understand the problem the statement is wrong for the following graph: Take 8 edges, connect each of 1,2,3,4 with each of 5,6,7,8, giving 16 connextions. The longest monotone path is 2, the average degree is 4.
|
| « Last Edit: Nov 10th, 2011, 1:25pm by Grimbal » |
IP Logged |
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
Yes, the average degree is the average # of edges that meet at a vertex. Also it is more clear to say arbitrary labeling rather than random labeling, so I will revise that in the problem statement.
The labels are also being assigned to edges, not to vertices. A path is considered monotone if the *edges* in that path are monotone.
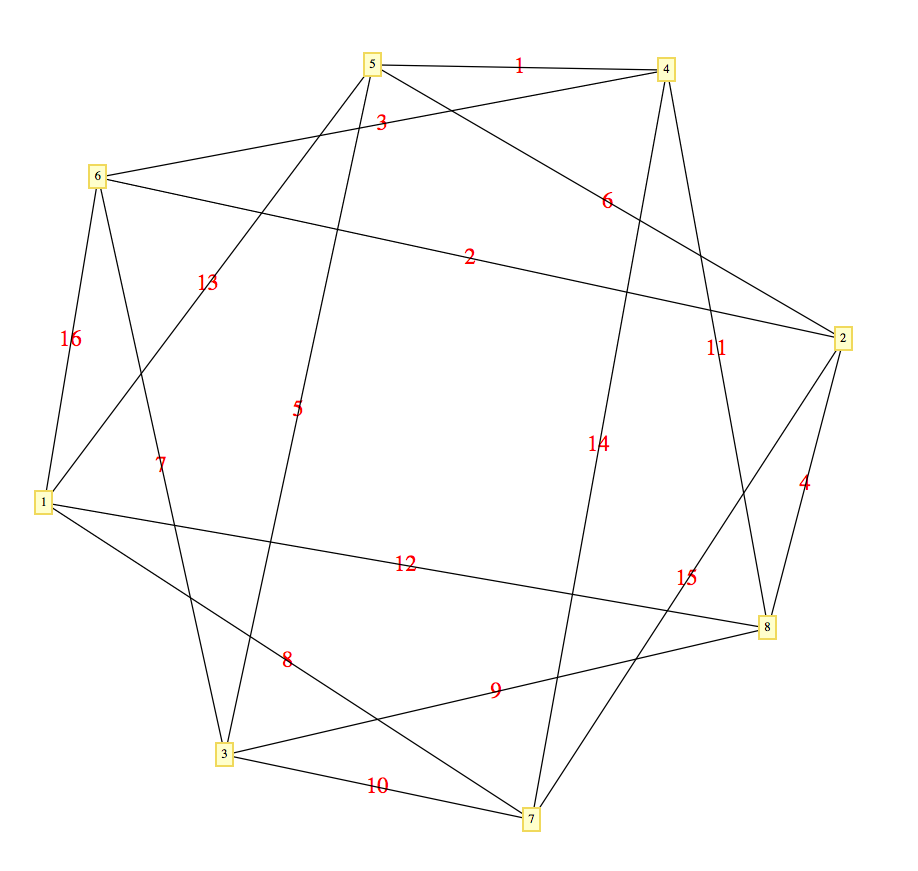
Attached is a visualization of the bipartite graph you mentioned, where the vertices {1,2,3,4} are complete to the vertices {5,6,7,8}. We see there are many monotone paths of length >= 4, such as the sequence of edges {1,3,7,9,11}. The sixteen distinct edge labels were assigned randomly without replacement.
|
| « Last Edit: Nov 10th, 2011, 11:16am by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: Monotone Paths in Graphs
« Reply #4 on: Nov 10th, 2011, 11:19am » |
Quote Modify
|
This problem may be too difficult without a hint, as I was simply told of the result:
Hint:
Imagine having a person standing on each vertex. A loudspeaker shouts the edges in sequence, and with each shout, the people move along the graph in a certain way.
|
| « Last Edit: Nov 10th, 2011, 11:19am by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Monotone Paths in Graphs
« Reply #5 on: Nov 10th, 2011, 1:24pm » |
Quote Modify
|
on Nov 10th, 2011, 11:15am, william wu wrote:| The labels are also being assigned to edges, not to vertices. A path is considered monotone if the *edges* in that path are monotone. |
|
I see. Sorry. I don't know why, I always mix up the words "edge" and "vertex" in english. Really annoying. I must have learnt it wrong the first time.
OK, Now I can start thinking about the problem.
|
| « Last Edit: Nov 10th, 2011, 1:30pm by Grimbal » |
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2874
|
|
Re: Monotone Paths in Graphs
« Reply #6 on: Nov 11th, 2011, 4:43am » |
Quote Modify
|
on Nov 10th, 2011, 11:19am, william wu wrote:This problem may be too difficult without a hint, as I was simply told of the result:
Hint:
Imagine having a person standing on each vertex. A loudspeaker shouts the edges in sequence, and with each shout, the people move along the graph in a certain way.
|
|
Well, that hint makes it obvious:
| hidden: |
Start with an empty pile of counters on each node. For each arc in order, swap the two piles at either end of the arc and add a counter to each. At the end of the process, each pile has followed a monotone path, of length equal to the number of counters in that pile.
Since the total number of counters is twice the number of arcs, which is also the sum of the degrees of the individual nodes, and the number of piles is the number of nodes, the average number of counters per pile is exactly equal to the average degree.
By the pigeonhole principle, at least one pile must have at least the average number of counters, so at least one pile must have traversed a path of length at least equal to the average degree. |
|
|
IP Logged |
|
|
|
Michael Dagg
Senior Riddler
Gender:
Posts: 500
|
|
Re: Monotone Paths in Graphs
« Reply #7 on: Nov 11th, 2011, 7:41am » |
Quote Modify
|
Excellent rmsgrey!
Ramsey theory generalizes the pigeonhole principle, guaranteeing
the existence of the required monotonic path. There are lots of fruitful
results in graph/group theory similarly derived.
|
|
IP Logged |
Regards,
Michael Dagg
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Monotone Paths in Graphs
« Reply #8 on: Nov 11th, 2011, 9:49am » |
Quote Modify
|
Very elegant proof, indeed!
|
|
IP Logged |
|
|
|
mgccl
Newbie
Posts: 1
|
|
Re: Monotone Paths in Graphs
« Reply #9 on: Feb 4th, 2013, 5:37pm » |
Quote Modify
|
on Nov 11th, 2011, 4:43am, rmsgrey wrote:
| hidden: |
At the end of the process, each pile has followed a monotone path, of length equal to the number of counters in that pile.
|
|
|
It followed a monotone walk instead of a path. Usually path means a simple path. So it is still unclear if the original statement is true.
|
| « Last Edit: Feb 4th, 2013, 5:39pm by mgccl » |
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2874
|
|
Re: Monotone Paths in Graphs
« Reply #10 on: Feb 5th, 2013, 4:34am » |
Quote Modify
|
on Feb 4th, 2013, 5:37pm, mgccl wrote:
It followed a monotone walk instead of a path. Usually path means a simple path. So it is still unclear if the original statement is true. |
|
True, there's no guarantee against loops in that proof.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print