 Author
Author |
Topic: log n and sigma 1/n (Read 3253 times) |
|
kaushiks.nitt
Newbie


Gender: 
Posts: 2
|
 |
log n and sigma 1/n
« on: Jun 13th, 2009, 10:28am » |
 Quote Quote  Modify Modify
|
I have this doubt regarding the Euler–Mascheroni constant γ . It is integral 1/[x] - 1/x limits from 1 to infinity and it is value is
0.57721 . Of cousre the big question that remains is if this is rational or not .
Let us say i keep splitting the limits i.e from 1 to 2 then 2 to 3 and so on from n to n+1 . I use limit n -> infinity.
The value would be like this 1 - (log 2 - log1 ) + 1/2 - ( log 3 - log 2) + ... 1/n - ( log (n+1) - log n ) = γ.
Firstly sigma 1/n should have been approx to log ( n+1) rather than log(n) .
In such a case the error would be .5 .
So why do we approx to me log(n) and what is the specialty of the constant .
|
|
 IP Logged IP Logged |
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: log n and sigma 1/n
« Reply #1 on: Jun 13th, 2009, 12:31pm » |
 Quote Quote  Modify Modify
|
The limit of (1 + 1/2 + ... + 1/n) - log n as n -> infty is the same thing as the limit of (1 + 1/2 + ... + 1/n) - log(n+1) as n -> infty, since the limit of log n - log(n+1) is 0 as n -> infty. So it doesn't make any difference either way.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: log n and sigma 1/n
« Reply #2 on: Jun 13th, 2009, 1:31pm » |
 Quote Quote  Modify Modify
|
If you want to be picky we should use
1+1/2+...+1/n ~ 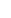 + log(n+1/2) + log(n+1/2)
for an O(1/n2) error, or more generally,
1+1/2+...+1/n ~ 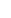 + log[ n+ 1/2 + 1/(24n) - 1/(48n3) + ... ] + log[ n+ 1/2 + 1/(24n) - 1/(48n3) + ... ]
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register