 Author
Author |
Topic: 157 (Read 1321 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
Find the smallest rational number x (smallest in the sense of smallest numerator and denominator) such that there exist rational numbers y and z and
x2 - 157 = y2
x2 + 157 = z2
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: 157
« Reply #1 on: Jul 4th, 2008, 10:42am » |
 Quote Quote  Modify Modify
|
It's Congruent!
|
|
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: 157
« Reply #2 on: Jul 4th, 2008, 11:21am » |
 Quote Quote  Modify Modify
|
157 is indeed congruent. Is that your final answer? 
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: 157
« Reply #3 on: Jul 5th, 2008, 7:24am » |
 Quote Quote  Modify Modify
|
Brute force (Google) search gives
x = 224403517704336969924557513090674863160948472041 / 17824664537857719176051070357934327140032961660.

|
| « Last Edit: Jul 5th, 2008, 7:29am by Eigenray » |
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: 157
« Reply #4 on: Jul 5th, 2008, 7:39am » |
 Quote Quote  Modify Modify
|
on Jul 5th, 2008, 7:24am, Eigenray wrote:Brute force (Google) search gives
x = 224403517704336969924557513090674863160948472041 / 17824664537857719176051070357934327140032961660.
 |
|
I was hoping it was Google-proof. What did you search for? I wonder what the fraction is for 2008. 
(I have thought of a good name for a porn search engine. How about Goggle?) 
|
| « Last Edit: Jul 5th, 2008, 5:09pm by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: 157
« Reply #6 on: Jul 5th, 2008, 10:28am » |
 Quote Quote  Modify Modify
|
on Jul 5th, 2008, 7:24am, Eigenray wrote:Brute force (Google) search gives
x = 224403517704336969924557513090674863160948472041 / 17824664537857719176051070357934327140032961660.
 |
|
The question is how to arrive at this answer? Using a complex derivation based on Elliptic Curves is one way; is there another (more elementary)?
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: 157
« Reply #7 on: Jul 5th, 2008, 11:28am » |
 Quote Quote  Modify Modify
|
I searched for '157 congruent'. The first result was wrong, so I tried searching both its numerator and denominator.
Let E be given by y2 = x3 - p2x. We are looking for a non-torsion point on this curve. I'm not sure how the point was actually found, but I'll tell you how one might find it, using the algorithm described in Silverman's "The Arithmetic of Elliptic Curves".
The complete 2-torsion of E, E[2], is (0,0), ( p,0), and the point at infinity. Since these are all rational, it turns out there is a bilinear pairing p,0), and the point at infinity. Since these are all rational, it turns out there is a bilinear pairing
E/2E x E[2]   */ */ *2. *2.
(The definition is a bit involved, but basically it is induced from the Weil pairing using the connecting homomorphisms of the Kummer sequences for  * and E.) * and E.)
But the image of this pairing is actually finite: it is contained in S = {  1, 1,  2, 2,  p, p,  2p }. Since E[2] = (Z/2Z)2 is also finite, we have an explicit embedding of E/2E into the finite group Hom(E[2], S) = S2. For each element of this group, we can try to find a point which maps to it, or prove there is no such point (but there is no known algorithm for this in general). But if we can figure out which elements of this group actually come from points on E, we get a set of representatives for the quotient E/2E, and a bit of work will give the generators for E. 2p }. Since E[2] = (Z/2Z)2 is also finite, we have an explicit embedding of E/2E into the finite group Hom(E[2], S) = S2. For each element of this group, we can try to find a point which maps to it, or prove there is no such point (but there is no known algorithm for this in general). But if we can figure out which elements of this group actually come from points on E, we get a set of representatives for the quotient E/2E, and a bit of work will give the generators for E.
So, what you actually try to do is find a point which maps to, say (-1, 1). If you look at the definitions, this amounts to trying to solve
a2 + b2 = 2p
a2 - c2 = p
in rationals. Note that it is similar to the system we started with. In practice, what is done is to repeatedly apply this procedure ("2-descent"), or more generally with an isogeny of degree 2. But in any case, this system has the solution
a=780871468723/53156661805
b=526771095761/53156661805
c=407598125202/53156661805.
(I found this by working backwards from the point on E, but in practice you would find this first.) Now
x = p-a2 = -166136231668185267540804 / 531566618052
y = -abc = -167661624456834335404812111469782006 / 531566618053
is a point on E. This point has x<0, but if we double it, we get a point with x-value
(224403517704336969924557513090674863160948472041 / 17824664537857719176051070357934327140032961660)2.
[edit]Thinking about it some more, we can start with the homogeneous space
Cp' : pw2 = p2 + p2/4 z4
for the curve E': y2 = x3 + p2/4 x. The point
(z,w) = (1143522/356441, 8345595903385/3564412)
on Cp' maps via 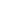 (z,w) = (p/z2, pw/z3) to (z,w) = (p/z2, pw/z3) to
(x,y) = (19946879277517/11435222, 467029870255557087245/11435223)
on E', which maps to
(x,y) = (69648970982596494254458225/4075981252022, 538962435089604615078004307258785218335/4075981252023)
on E under the isogeny  (x,y) = ((y/x)2, y(p2/(4x2)-1)). (x,y) = ((y/x)2, y(p2/(4x2)-1)).
This point then doubles to the same point. However, to continue the descent on Cp' requires passing to a larger number field I think.
|
| « Last Edit: Jul 5th, 2008, 1:36pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: 157
« Reply #8 on: Jul 5th, 2008, 5:34pm » |
 Quote Quote  Modify Modify
|
Yes, that's the proof I was thinking of.  
You are amazing, Eigenray! 
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Benny
Uberpuzzler
    

Gender: 
Posts: 1024
|
 |
Re: 157
« Reply #9 on: Jul 7th, 2008, 3:08pm » |
 Quote Quote  Modify Modify
|
Thanks Eigenray,
You can also find an interesting discussion of the congruent number problem at
http://www.math.umd.edu/~eve/cong_num.html
|
|
 IP Logged IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: 157
« Reply #10 on: Jul 7th, 2008, 9:55pm » |
 Quote Quote  Modify Modify
|
on Jul 7th, 2008, 3:08pm, BenVitale wrote:
Thanks for the link.
You would make a good researcher, Ben. Poacher turned gamekeeper, so to speak. LOL
|
| « Last Edit: Jul 8th, 2008, 1:31am by ThudnBlunder » |
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: 157
« Reply #11 on: Jul 8th, 2008, 12:56am » |
 Quote Quote  Modify Modify
|
Another good article is this.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: 157
« Reply #12 on: Jul 8th, 2008, 4:35am » |
 Quote Quote  Modify Modify
|
on Jul 7th, 2008, 3:08pm, BenVitale wrote:
Yes that's the one that has a typo in the numerator.
Googling some more I found this (pagina 19, ejemplo 6.8). So it is done via 2-isogeny:
Original curve E : y2 = x3 - p2x
Auxiliary curve E' : y2 = x3 + 4p2x
Homogeneous space Cd : dw2 = d2 + 4p2z4, d  { { 1, 1,  2, 2,  p, p,  2p}. 2p}.
According to that pdf, for the curve Cp, we parameterize
w2 = p(1+4Z2)
[It is a conic, so we can find one solution, say Z0=3/11 (since p = 112 + 4*32); then set w=w0+ut, Z=Z0+vt, and eliminate t, giving Z in terms of integers u,v.] Then use this parameterization to find a solution where Z=z2 is a square, and map it back to a point on E. There must be a way to optimize this though because the required (u,v) are either (7687738, 49921) or (2768294, 322213), and it seems like those would take as long to find as testing each z.
Note that the maps are elementary: that is, if we find a point on an associated homogeneous space it's easy to see we get a point on E; the hard part is proving that [mod the image of the dual isogeny] any point of E comes from one of these. In fact I recall reading somewhere that when Euler(?) proved y2 = x3 + 1 has no 'non-trivial' solutions [(2,3) generates the order 6 torsion subgroup], he was really using 2-isogenies, though of course that's not what they were called at the time. I believe some of Fermat's descent falls into this category too.
|
| « Last Edit: Jul 8th, 2008, 4:53am by Eigenray » |
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register