Author |
Topic: An IMO question: (4ab-1) | (4a^2 - 1)^2 (Read 5765 times) |
|
wonderful
Full Member
Posts: 203
|
 |
An IMO question: (4ab-1) | (4a^2 - 1)^2
« on: May 29th, 2008, 6:39pm » |
 Quote  Modify
|
Let a and b be positive integers. Show that if (4ab-1) divides (4a^2 - 1)^2 , then a=b.
Have A Great Day!
Source: IMO
|
| « Last Edit: Jun 11th, 2008, 5:12pm by wonderful » |
 IP Logged |
|
|
|
ecoist
Senior Riddler
Gender: 
Posts: 405
|
|
Re: a, b postive integers
« Reply #1 on: Jun 6th, 2008, 8:31pm » |
Quote Modify
|
I bet everyone interested has observed this. 4ab-1 divides (a-b)2 and therefore also divides (4b2-1)2.
|
|
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: a, b postive integers
« Reply #2 on: Jun 8th, 2008, 10:57am » |
Quote Modify
|
We can also show that there if 4ab-1 divides (4a^2-1)^2 and (b =/= a), then there must be some b' < a such that 4ab'-1 divides (4a^2-1)^2, which combined with your observation would give us an infinite decreasing sequence of natural numbers...
To show that there is a b' < a:
We can show that (4a^2-1)^2/(4ab-1) must be of the form 4ab' - 1 with 0 < b' < a, if b > a.
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: a, b postive integers
« Reply #3 on: Jun 9th, 2008, 2:43pm » |
Quote Modify
|
Wow, Aryabhatta, you can squeeze blood from a turnip! I thought my observation was hardly worth posting.
|
|
IP Logged |
|
|
|
wonderful
Full Member
Posts: 203
|
This question may have sevaral solution. For those who are interested, attached is a nice solution.
Have A Great Day!
|
| « Last Edit: Jun 10th, 2008, 5:41pm by wonderful » |
IP Logged |
|
|
|
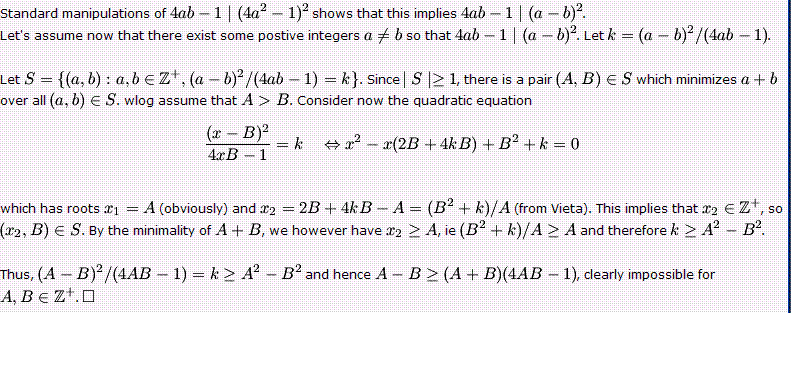
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: a, b postive integers
« Reply #5 on: Jun 11th, 2008, 4:48pm » |
Quote Modify
|
Pray tell, what's the "4" for? Seems irrelevant to both proofs. Sorry, still fascinated by both the problem and Aryabhatta's proof. (And isn't it time to correct the spelling in the title?)
|
|
IP Logged |
|
|
|
Aryabhatta
Uberpuzzler
Gender:
Posts: 1321
|
|
Re: An IMO question: (4ab-1) | (4a^2 - 1)^2
« Reply #6 on: Jun 18th, 2008, 7:21pm » |
Quote Modify
|
Sorry, i lost track of this.
ecoist, i guess i just got lucky. If had posted my observation before you did, i am sure you would have completed the proof...
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: An IMO question: (4ab-1) | (4a^2 - 1)^2
« Reply #7 on: Jun 18th, 2008, 8:32pm » |
Quote Modify
|
Like Tiger Woods winning his 14th major golf tournament, talented people are often lucky, Aryabhatta! Even though I considered infinite descent, your simple solution never occured to me.
|
|
IP Logged |
|
|
|
Hippo
Uberpuzzler
Gender:
Posts: 919
|
|
Re: An IMO question: (4ab-1) | (4a^2 - 1)^2
« Reply #8 on: Jun 18th, 2008, 10:22pm » |
Quote Modify
|
I didn't think about it much, but I don't understand the Aryabatta's proof:
... there is no a-b symmetry and b>a -> b'<a.
How do you gain b''?
|
|
IP Logged |
|
|
|
ecoist
Senior Riddler
Gender:
Posts: 405
|
|
Re: An IMO question: (4ab-1) | (4a^2 - 1)^2
« Reply #9 on: Jun 19th, 2008, 10:00am » |
Quote Modify
|
There is symmetry, Hippo, because 4ab-1 also divides (4b2-1)2 (see my post)! Hence Aryabhatta can assume that b>a if a=/=b. Then he shows that there exists b'<a such that the pair {a,b'} satisfies the same conditions (including b>a) as the pair {a,b}, with b' as the new "a" and a as the new "b". It now follows that there is a b''<b', which pair {b'',b'} also satisfies the same conditions with b'' as the new "a" and b' as the new "b".
|
|
IP Logged |
|
|
|
Hippo
Uberpuzzler
Gender:
Posts: 919
|
|
Re: An IMO question: (4ab-1) | (4a^2 - 1)^2
« Reply #10 on: Jun 19th, 2008, 3:43pm » |
Quote Modify
|
OK ... thanks for explanation.
P.S.: Now I get the time to look at it ... nice  ... symmetry 16a2b2(a-b)2 =
(4ab-1)(4ab3 + b2 - 8a2b2) + (4a2-1)2
|
| « Last Edit: Jun 20th, 2008, 1:13am by Hippo » |
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print