 Author
Author |
Topic: Math Conference Dining Rooms (Read 2213 times) |
|
william wu
wu::riddles Administrator
    


Gender: 
Posts: 1291
|
 |
Math Conference Dining Rooms
« on: May 5th, 2008, 7:06pm » |
 Quote Quote  Modify Modify
|
From the recent USAMO 2008:
At a certain mathematical conference, every pair of mathematicians are either friends or strangers. At mealtime, every participant eats in one of two large dining rooms. Each mathematician insists upon eating in a room which contains an even number of his or her friends. Prove that the number of ways that the mathematicians may be split between the two rooms is a power of two.
|
|
 IP Logged IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Math Conference Dining Rooms
« Reply #1 on: May 5th, 2008, 9:03pm » |
 Quote Quote  Modify Modify
|
Interesting. I think the hard part is to show that there is at least one solution.
This could fail in two ways, for stupid values of 'friend':
Self-friendship, e.g., A is friends with himself, but there are no other friends.
Non-symmetric, e.g., everybody has A and B as a friend, but there are no other friends (for at least 3 people).
But if friendship is symmetric, and there are no self-friends, it looks like there is always a solution.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Math Conference Dining Rooms
« Reply #2 on: May 5th, 2008, 10:49pm » |
 Quote Quote  Modify Modify
|
Here is a non-constructive proof:
| hidden: | Everything here is mod 2. Let A be the friendship matrix. If vi = 0 or 1 is the room person i belongs to, then the number of friends of person i in the same room is
vi Aijvj + (1-vi) Aijvj + (1-vi) Aij(1-vj) Aij(1-vj)
=  Aij (1+vi+vj) Aij (1+vi+vj)
= si + sivi + (Av)i,
where si is the sum of the i-th row of A. Letting S be the diagonal matrix on s, we need to find a vector v such that (A+S)v = s. So if there exists one solution, any two solutions differ by an element of the null space of (A+S). Since this is a vector space over the field of 2 elements, its order is a power of 2.
To show there exists a solution, we show that rank(A+S) = rank([A+S; s]) by showing that (A+S) and [A+S; s] have the same left null space. Since A,S are symmetric, this is equivalent to showing that Aw = Sw implies <w,s>=0.
Suppose Aw=Sw, and let W = { i : wi = 1}. Then for each i 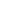 W, W,
 {j {j W} Aij = W} Aij =  j Aijwj = (Aw)i = (Sw)i = siwi = 0. j Aijwj = (Aw)i = (Sw)i = siwi = 0.
So in particular  {i {i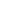 W; j W; j W} Aij = 0. And since A is symmetric, W} Aij = 0. And since A is symmetric,  {i {i W; j W; j W} Aij = 0. Therefore W} Aij = 0. Therefore
0 =  {i {i W; j W; j W} Aij + W} Aij +  {i {i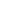 W; j W; j W} Aij W} Aij
=  {i; j {i; j W} Aij W} Aij
=  j wjsj, j wjsj,
as required. |
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Math Conference Dining Rooms
« Reply #4 on: May 6th, 2008, 12:06am » |
 Quote Quote  Modify Modify
|
Aha, yes, it's actually equivalent to the hint you posted here.
But we can also use 'Proposition 1' here to finish the proof: (A+S)v = s has a solution, because s is the diagonal of A+S.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register