Author |
Topic: Sink the (real) sub (Read 1543 times) |
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender: 
Posts: 1948
|
 |
Sink the (real) sub
« on: Feb 13th, 2008, 1:25am » |
 Quote  Modify
|
Much like Sink the Sub, an enemy sub is moving somewhere on the real line with unknown (constant) velocity, and you can launch one torpedo every minute. If the position and velocity can be arbitrary real numbers now, then it's impossible to be guaranteed to hit it exactly. But that's okay, because the sub is not a point mass: it has some positive radius.
(A) Devise a strategy that is guaranteed to eventually hit the sub, if the size of the sub is known.
(B) Can you find a strategy that works if the size of the sub is unknown?
(C) Can you find a strategy that works if the sub were moving with constant acceleration instead?
(D) Can you find a strategy that works if the sub were moving with constant velocity in the plane instead?
|
| « Last Edit: Feb 13th, 2008, 4:07pm by Eigenray » |
 IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Sink the (real) sub
« Reply #1 on: Feb 16th, 2008, 11:12am » |
Quote Modify
|
In other words, part (A) is asking you to prove:
for all r > 0, there exists a sequence of real numbers (xn) such that for all real numbers p,v, there exists an n such that |p+nv-xn| < r.
Part (B) asks if this holds with the first two quantifiers reversed.
|
| « Last Edit: Feb 22nd, 2008, 4:22pm by Eigenray » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Sink the (real) sub
« Reply #2 on: Feb 22nd, 2008, 4:34pm » |
Quote Modify
|
Any thoughts? Too hard? Too boring? Too confusing? You might find (C) to be the easiest one:
(C) Is there a sequence of real numbers (xn) such that for all real numbers p,v,a, there exists an n such that |p+nv+an2 - xn| < 1?
(D) Is there a sequence of vectors (Xn)   2 such that for all vectors P,V 2, there exists an n such that |P+nV - Xn| < 1?
And a followup to parts A,B:
(E) Let f(n) be a (fixed, known) function of n, and suppose the sub's position is given by r(n) = a + bf(n), for unknown a,b. When does there exist a strategy that works?
|
| « Last Edit: Feb 22nd, 2008, 9:32pm by Eigenray » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Sink the (real) sub
« Reply #3 on: Feb 29th, 2008, 11:45pm » |
Quote Modify
|
Anybody tried this?
Hint: if you fix n and xn, what do the regions |p+nv-xn|<1 and |p+nv+an2-xn|<1 look like?
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Sink the (real) sub
« Reply #4 on: Mar 1st, 2008, 11:44am » |
Quote Modify
|
For (A), I think this idea works, but don't have the time to pursue it anymore right now: As indicated by Eigenray's last post, first of all it is sufficient to consider the case of r = 1. Look at the vp plane. Choose x1 = 0. This catches all points (v,p) in a  2 - wide strip centered on the line p=v. Now suppose you have chosen the values for {xi} for i < n. These values catch points in the plane lying in strips of width 2/(i2+1). Choose among the nearest points to the origin that are not in any of the strips, and choose xn in such away as to cover as much area around these points as possible.
As n increases, so does the radius of the covered disk about the origin. If you do it right, the radius should -->  .
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Sink the (real) sub
« Reply #5 on: Mar 1st, 2008, 9:38pm » |
Quote Modify
|
on Mar 1st, 2008, 11:44am, Icarus wrote:| If you do it right, the radius should --> . |
|
That's the idea. It suffices to use only a small part of each strip, which makes it simpler (but not too small a part: taking a square from each strip, you can't cover the plane).
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Sink the (real) sub
« Reply #6 on: Mar 16th, 2008, 7:00pm » |
Quote Modify
|
I haven't made any more progress on this, but hate to see it slip into obscurity nearly as much as Eigenray seems to.
While Eigenray has confirmed that my initial direction is correct, it is evident to me that I am still in need of an additional insight, as I have not been able to demonstrate that the minimal covered radius can be forced to increase without bound.
Perhaps someone such as Hippo, Obob, or SWF can step in where I have failed?
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Hippo
Uberpuzzler
Gender:
Posts: 919
|
|
Re: Sink the (real) sub
« Reply #7 on: Mar 17th, 2008, 4:14am » |
Quote Modify
|
on Mar 16th, 2008, 7:00pm, Icarus wrote:| Perhaps someone such as Hippo, Obob, or SWF can step in where I have failed? |
|
Wow, what a credit to be named (and first even more), thanks Icarus  ... I didn't thing about the problem at all yet. ... may be later 
|
| « Last Edit: Mar 17th, 2008, 4:16am by Hippo » |
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: Sink the (real) sub
« Reply #8 on: Mar 17th, 2008, 2:03pm » |
Quote Modify
|
I think this works for (A).
As before, let p be the initial starting position and v the velocity of the sub. We need to produce a sequence xn such that the sets Sn = {(p,v):|p+nv-xn| 1} cover the pv-plane. This is because it is enough to solve the problem when r=1+e for some small e, but then we can replace the < sign with a sign by instead requiring that we hit a sub of radius 1+e within 1 unit.
Now write the pv-plane as the union of the squares Tn={(p,v):|p|n, |v|n}. We show that given any index n and any number N (presumably very large), there is a choice of points xN,xN+1,...,xN+k for some finite k (dependent on n and N) such that the corresponding sets SN,...,SN+k cover Tn. If we can prove this, then we will form a full sequence xn as follows: we use finitely many xn to cover T1. Then we use finitely many more to cover T2, finitely many more to cover T3, etc. In the end we construct a sequence exhausting the whole pv-plane, and the problem is solved.
The preceding steps were all purely formal; now the geometry comes in. Suppose we fix p, n and xn. Then the region Sn restricted to the line p=constant is described as those v such that (xn-p-1)/n v (xn-p+1)/n. Thus the intersection of Sn with the line p=constant is a line segment centered about v=(xn-p)/n and of radius 1/n about the center. The geometric description of the whole region Sn is therefore that Sn is the region surrounding the line v=(xn-p)/n of vertical width 2/n (where p is considered the horizontal direction and v the vertical direction). Reversing this calculation (i.e. holding v fixed), we get that the horizontal width of the strip is 2. Letting xn vary, we see that by choosing xn appropriately, Sn can be taken to be any region centered about a line of slope -1/n in the pv-plane whose vertical width is 2/n and whose horizontal width is 2.
With this geometric description of Sn out of the way, we proceed with the proof of the result alluded to in the third paragraph. Namely, given an index n and a number N, we construct a finite sequence xN,xN+1,...,xN+k such that the sets SN,SN+1,...,SN+k cover the square Tn. We do this as follows. Consider the top edge of Tn and the left edge of Tn. Let xN be such that the line SN is centered about passes through the top edge of Tn one unit left of the top right corner of the square. Recall that the horizontal width of SN is 2. So all the points of the top edge of Tn within one unit of the intercept of the line Sn is centered about are contained in Sn. Pick the next point xN+1 so that the line Sn+1 is centered about meets the top edge 3 units to the left of the right. Continuing in this manner by picking xi's so that the corresponding lines are spaced 2 units apart, we cover the entire top edge of the square using the corresponding sets. Next, we do a similar thing with the left edge of the square. Things here are more tricky though, since the vertical width of the strips is 2/n (in particular, it decreases each step of the way) instead of 2. We want to cover the whole left edge using the sets xn, in an exactly analogous manner to how we covered the top edge. However, this can be done because the harmonic series diverges. At the end of the edge things may not line up perfectly, but we can just throw in an x value such that the corresponding line meets the lower left corner of the square.
Now we have constructed a finite sequence xN,...,xN+k whose corresponding sets SN,...,SN+k cover the top and left edge of the square Tn. The claim is that these sets cover the whole square. The essential reason for this is that the slopes of the lines corresponding to the xi's are increasing as i increases. The union of the first j sets SN,...,SN+j looks like the region between the graph of a decreasing function from [-n,n] to [-n,n] and the top edge of the square Tn; the function in question is the minimum of the v-values of the bottom lines of the first j regions SN,...,SN+j. But the lower-left corner of the square is in the union of all the sets, and the only decreasing function from [-n,n] to [-n,n] with f(-n)=-n is the constant function f(x)=-n. So the union of all the sets is the whole square, as was to be shown.
Its interesting that the easier integer version of this problem follows from the basic set theory remark that the product of two countable sets is countable, whereas there is some real geometry lurking in this problem.
|
| « Last Edit: Mar 17th, 2008, 2:03pm by Obob » |
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: Sink the (real) sub
« Reply #9 on: Mar 17th, 2008, 2:30pm » |
Quote Modify
|
And (C) appears impossible.
Consider pva-space, and the obvious definition for Sn corresponding to a choice of point xn (as in my last post). Then Sn is the region in pva-space centered about a plane with thickness in the a-direction of 2/n2. Consider the intersection of Sn with some cube Tk, analogous to defined in my previous post. For each choice of p,v, there is at most one point (p,v,a) contained in the central plane of Sn. So the volume of Sn intersected with Tk is at most the area of one side of Tk times the thickness 2/n2 of Sn in the a-direction. This is (2k)2 . 2/n2. Then volume of the union of the Sn intersected with Tk is at most the sum of the volumes of all the regions Sn  Tk, which is at most a constant C (independent of k, and coming from the convergence of  1/n^2) times k2. If we choose k to be sufficiently large, then (2k)3 (the volume of Tk) is bigger than C k2. That is, it is impossible for any choice of a sequence xn to correspond to a set of regions Sn covering Tk. So the sets Sn cannot cover all of pva-space, and no strategy will always hit the sub if it has unknown constant acceleration, initial velocity and initial position.
In fact, even if we know the initial velocity, the same argument shows that there is no strategy. There is just one less factor of k floating around.
|
| « Last Edit: Mar 17th, 2008, 2:32pm by Obob » |
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: Sink the (real) sub
« Reply #10 on: Mar 17th, 2008, 2:59pm » |
Quote Modify
|
(B) should be possible. The key is the step in my proof of (A) where we show that the square Tn can be covered by finitely many regions SN,...,SN+k, no matter what N is. Recalling that the solution for r=1 is equivalent to the solution for arbitrary r by a scaling argument, we proceed as follows. First cover T1 corresponding to a radius of r=1. Next cover T2 corresponding to a radius of r=1. Next cover T1 corresponding to a radius of r=1/2. Next cover T3 corresponding to r=1, T2 corresponding to r=1/2, and T1 corresponding to r=1/3. Continuing in this fashion, we eventually cover Tn corresponding to a radius of 1/k for all n,k, which means that no matter the radius of the sub we will eventually hit it.
Anybody care to tackle D?
|
| « Last Edit: Mar 17th, 2008, 3:00pm by Obob » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Sink the (real) sub
« Reply #11 on: Mar 17th, 2008, 3:08pm » |
Quote Modify
|
Excellent. My construction for (A) isn't as 'efficient' as yours, but I think it's simpler (for me, anyway, since I don't have much intuition for geometry):
To make |p+nv - xn| < 1, it suffices to estimate p within 1/2, and v within 1/2n. Thus the strip contains a 1 x 1/n rectangle (this is actually the largest axes-parallel rectangle in the strip). These still do the job, but are much easier to work with.
Note that for (C), the proof shows that, even if we know the initial velocity, and a bound on the initial position and acceleration, we still may not be able to sink the sub.
I think you must know the answer to E by now.
|
|
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: Sink the (real) sub
« Reply #12 on: Mar 17th, 2008, 3:38pm » |
Quote Modify
|
Ah yes, Eigenray. Using that Sn can be made to contain any 1 x 1/n strip does make things easier. And efficiency isn't too important really, since in all likelihood it will take a very very long time. Using 1 x 1/n strips you could also avoid recovering the previous square each step of the way, as I did in my solution.
I haven't given any thought to (E) yet. I have real work to do, unfortunately, and shouldn't think about it now.
|
|
IP Logged |
|
|
|
Hippo
Uberpuzzler
Gender:
Posts: 919
|
|
Re: Sink the (real) sub
« Reply #13 on: Mar 18th, 2008, 6:04am » |
Quote Modify
|
Good job Obob. I thought about it some minutes. The strips with changing slopes are natural reformulation but I have missed the geometrical part ... the top, left covering strategy.
(I was thinking about covering of the nearest uncovered point instead but I have not spent much time on it).
So only the divergence of "unit errors" ... 1/n resp. 1/n^2 matters for the one dimensional case.
So what about (D): I am very weak in geometry, especially in 4D  . Our initial configuration is plane of positions times plane of velocities.
n-th hit hits 4D "stripe" with unit square slices in the plane of positions with the slant defined by velocity cordinates. My (weak) intuition says that covering the 4dimensional cubes differnce by top "3Dedge", left "3D edge", ... will fail as in one 3Dedge the increments are with two of three cordinates going along the edge are 1/n long so the 1/n^2 increments does not diverge to allow its filling (the total volume of intersections with the 4D nxnxnxn cube is less than n^4 for sufficintly large n).
|
| « Last Edit: Mar 18th, 2008, 6:07am by Hippo » |
IP Logged |
|
|
|
Hippo
Uberpuzzler
Gender:
Posts: 919
|
|
Re: Sink the (real) sub
« Reply #14 on: Mar 19th, 2008, 12:50am » |
Quote Modify
|
Actually the arguments can be supported by solving "easier" puzzle:
Sub starts at position 0 resp 02, and the velocity (resp. acceleration) is unknown.
You shoot a torpedo per minute starting at time 1.
So we reduce the unknown initial position and with the velocity plane for (D) we don't need 4D.
A shot at time n covers disk (ball) of radii 1/n of the velocities. So its area is c/n2. Sum of it converges so we never cover the whole plane.
For the 1D speed the "area/length" is 1/n. As sum of it diverges we can cover all starting configurations. Actually we can as well cover countable number of planes (corresponding to all unit shifts of the initial position).
For the acceleration the shot at time n covers ball of radii 1/n^2 of accelerations. So the sum of "areas" converges even for the 1D case and we are not able to cover all starting configurations.
Interesting thing is that even for unknown acceleration and velocity in 2D there is no problem to cover all rational initial positions so the dense subset of configurations is solvable.
|
| « Last Edit: Mar 19th, 2008, 12:51am by Hippo » |
IP Logged |
|
|
|
Obob
Senior Riddler
Gender:
Posts: 489
|
|
Re: Sink the (real) sub
« Reply #15 on: Mar 19th, 2008, 5:55am » |
Quote Modify
|
Very nice, Hippo!
|
|
IP Logged |
|
|
|
Hippo
Uberpuzzler
Gender:
Posts: 919
|
|
Re: Sink the (real) sub
« Reply #16 on: Mar 19th, 2008, 9:13am » |
Quote Modify
|
Thanks , I think the problem is exhausted ... there are only small variants ...
(F) the constant speed is known, but the direction unknown for 2D case (we have already seen it does not play role if the original position is known or not).
Or the cadence is a function of time. Say increasing linearly.
But I think its the same level of complexity as the others and the solution is as obvious as them.
Ooops, there is the (E) case served by Eigenray ... he surprises me all the time
So as the a is unimportant we solve the unknown b times known f(n). Shoot at time n fills ball(interval) of length 1/|f(n)|. And we need the sum of the areas(lengths) to diverge. So 1/|f(n)| should be divergent in the 1D case and 1/|f^2(n)| divergent in the 2D case. So bouned by f1(n)=n\log n\loglog n\logloglog n ... for the 1D case and by f2=f1 for the 2D case.
|
| « Last Edit: Mar 19th, 2008, 9:32am by Hippo » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Sink the (real) sub
« Reply #17 on: Mar 19th, 2008, 2:33pm » |
Quote Modify
|
Very nice indeed!
For (D) I had solved it by fixing one coordinate of P. Then |P+nV-Xn|<1 is a cylinder in R3 with cross sectional area 1/n2, so these will not cover R3 for a reason very similar to the 'slabs' of thickness 1/n2 as in (C).
But I hadn't realized that the starting position is irrelevant in the same way the radius of the sub is, i.e., if we can solve it with known starting position and radius, then we can solve the more general case (and conversely, of course).
So here's my final followup:
Fix a positive increasing function f : 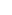  +, and suppose the position of the sub is P + f(n)C, with P,C d.
(1) If we can solve it when P and the radius are known, show that we can solve it when they are unknown.
(2) Show that the above problem is solvable iff f(n)-d diverges. (Trickier than it sounds, I think.)
|
| « Last Edit: Mar 19th, 2008, 3:40pm by Eigenray » |
IP Logged |
|
|
|
Hippo
Uberpuzzler
Gender:
Posts: 919
|
|
Re: Sink the (real) sub
« Reply #18 on: Mar 19th, 2008, 5:24pm » |
Quote Modify
|
Happy to realize what you don't Eigenray but actually I cannot see where is the problem in (2).
As f(n)-d diverges the ball hits can cover whole initial space for C for a fixed P.
(at least it has sufficient total volume, I didn't actually experiment with the filling strategy, but its sufficient to show that hypercubes with size n can be covered for an arbitrary high N (Obobs proof method) I am week in highD geometry so if there should be extremely large overlaps it can make problems, but I don't expect it would be problem as for high n the ball radii will be almost equal and you can approximate the balls with hypercubes with volume decreased only by constant factor so the overlaps would be only at most constant factor of the balls total volume).
But as it diverges we can extend the hypercube by position cordinates to efectively cover all C spaces for countable number of unit shifts of the fixed P.
Actually we didn't cover initial space for C for a fix point position P but a for a fixed unit disk (sub contains 2 units disk in this case).
Oh ... now I understand the (1) question ... I takes me long time sometimes ... How to solve the riddle if the hit ball size is unknown ... increasing C by same constant is simillar as decreasing the sub size (the same hit volume) but in the former case we have problems as we are blind at ball positioninig. But we can "simultaneously" solve the problem for radii 2-i.
... Add the i dimension to Obob's hypercube in the proof.
OK if you find another nontrivial extension I would be very surprised.
BTW: I wouldn't expect this problem can be so funny
|
| « Last Edit: Mar 19th, 2008, 5:24pm by Hippo » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Sink the (real) sub
« Reply #19 on: Mar 20th, 2008, 3:08am » |
Quote Modify
|
Well, that's the tricky bit, proving that if the sum of the d-volumes of a set of balls in d is infinite, then they cover d. It is 'obviously' true, but it's not obvious how to prove it.
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
|
Re: Sink the (real) sub
« Reply #20 on: Mar 20th, 2008, 9:42am » |
Quote Modify
|
on Mar 20th, 2008, 3:08am, Eigenray wrote:| Well, that's the tricky bit, proving that if the sum of the d-volumes of a set of balls in d is infinite, then they cover d. It is 'obviously' true, but it's not obvious how to prove it. |
|
Either I'm missing something, or it's obviously not true - for example, consider the area of the region between y=1 and y=-1 - an infinite area that fails completely to cover the plane...
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Sink the (real) sub
« Reply #21 on: Mar 20th, 2008, 11:09am » |
Quote Modify
|
I thought of that too, but in this case we can choose the center of each ball, so, if I understand correctly, the question is to prove that, given a set of balls in d the sum of whose d-volumes is transfinite, it is possible to cover d. Right?
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Sink the (real) sub
« Reply #22 on: Mar 20th, 2008, 1:15pm » |
Quote Modify
|
Yes, we have a set of physical d-dimensional balls with infinite combined volume. We can put them wherever we like.
Also, it's important that they be balls, instead of things like n by 1/n2 rectangles, which won't cover.
So we can replace them with cubes. It suffices to show inductively that for each d, there is a constant C such that whenever any set of d-cubes has d-volume > C, they will cover the unit d-cube. But I wonder if there isn't a simpler way. This must be a well-known problem.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print