 Author
Author |
Topic: randomness (Read 4594 times) |
|
Benny
Uberpuzzler
    

Gender: 
Posts: 1024
|
Gregory J. Chaitin stated, "Although randomness can be precisely defined and can even be measured, a given number cannot be proved to be random. This enigma establishes a limit to what is possible in mathematics. "
Does there exist a mathematical definition of randomness, and if so what is it? Furthermore, when one wishes to prove that a given sequence of say integers is random, then what is it that they would have to show?
Finally, is it possible that a precise (mathematical) definition of randomness is impossible?
|
|
 IP Logged IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: randomness
« Reply #1 on: Feb 12th, 2008, 1:03am » |
 Quote Quote  Modify Modify
|
There exists a "Kolmogorov complexity".
If you fixed a programming language.
Each computation is started with a code and initial data. For each such pair (code,data) measure their length.
Each such pair generates one sequence.
Measure the complexity of a sequence by the size of the minimal pair of code and data generaing it. Random sequences are those where in optimal pair the code is empty.
|
| « Last Edit: Feb 12th, 2008, 2:10am by Hippo » |
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: randomness
« Reply #2 on: Feb 12th, 2008, 2:05am » |
 Quote Quote  Modify Modify
|
[obsolete]... where the shortest program is as long as the sequence it generates.[/obsolete]
While that definition works well in practice, it doesn't help to prove randomness of a sequence because that definition depends on a specific programming language. For every sequence you can design a language that generates that sequence in a single instruction. So every sequence would be non-random in some programming language. That means that the definition is not universal.
|
| « Last Edit: Feb 13th, 2008, 9:12am by Grimbal » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: randomness
« Reply #3 on: Feb 12th, 2008, 2:13am » |
 Quote Quote  Modify Modify
|
Yes: I thing Kolmogorov uses Turing machines with explicit restrictions so the model is fixed and rather "natural", but I agree this condition is not testable by a computer (halting problem involved).
|
| « Last Edit: Feb 12th, 2008, 2:18am by Hippo » |
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: randomness
« Reply #4 on: Feb 12th, 2008, 2:36am » |
 Quote Quote  Modify Modify
|
Entropy is a good way to measure randomness.
And there are tons of statistical tests you can use (e.g. chi-square test)
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: randomness
« Reply #5 on: Feb 13th, 2008, 8:17am » |
 Quote Quote  Modify Modify
|
... yes these tests conjecture some kind of nonrandomness and statisticaly proves that the conjecture holds with high probability.
... they cannot guarantee randomness!
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: randomness
« Reply #6 on: Feb 13th, 2008, 8:50am » |
 Quote Quote  Modify Modify
|
on Feb 13th, 2008, 8:17am, Hippo wrote:... yes these tests conjecture some kind of nonrandomness and statisticaly proves that the conjecture holds with high probability.
... they cannot guarantee randomness! |
|
No amount of measures can guarantee randomness. There is no way to tell a random sequence apart from a well crafted sequence made to look random.
A computers pseudo random number generator is not random, yet pretty much any measure of randomness you can unleash on it would say it produces random numbers.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: randomness
« Reply #7 on: Feb 13th, 2008, 10:27am » |
 Quote Quote  Modify Modify
|
on Feb 13th, 2008, 8:50am, towr wrote:
No amount of measures can guarantee randomness. There is no way to tell a random sequence apart from a well crafted sequence made to look random.
A computers pseudo random number generator is not random, yet pretty much any measure of randomness you can unleash on it would say it produces random numbers. |
|
This again correspond to conclussions from Kolmogorov ... there are cases when we can prove the sequence is not random, but to prove it's random is uncomputable.
Probably statistical property which proves nonrandomness can be used for "wavelet kind" packing so there is close correspondence
(for long enough sequences).
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
on Feb 13th, 2008, 10:27am, Hippo wrote:| ... there are cases when we can prove the sequence is not random ... |
|
Can we? I do not think so; we can never be completely sure that any given sequence is not the result of some random process.
|
| « Last Edit: Feb 13th, 2008, 10:46am by pex » |
 IP Logged IP Logged |

|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: randomness
« Reply #9 on: Feb 13th, 2008, 1:01pm » |
 Quote Quote  Modify Modify
|
A sequence of twenty consecutive heads might not seem random, but it should occur once every 220 runs; just the same as any 20-coin sequence.
And similar things can be said for any kind of sequence.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: randomness
« Reply #10 on: Feb 13th, 2008, 4:03pm » |
 Quote Quote  Modify Modify
|
on Feb 13th, 2008, 8:50am, towr wrote:| A computers pseudo random number generator is not random, yet pretty much any measure of randomness you can unleash on it would say it produces random numbers. |
|
Except, of course, for algorithmic randomness. There are several 'natural' ways to define algorithmically random that all end up being equivalent, which makes this a good definition (much like there are several equivalent ways to define an algorithm or computable function).
Of course, for any sequence, there exists a function whose output is that sequence, but this function will almost always be non-computable. And if a sequence is computable, then it's not algorithmically random. But there are of course non-computable sequences which aren't algorithmically random too: let X = (xi) be an infinite binary sequence with x2i=0 for all i. There are uncountably many such sequences, so most of them are non-computable. But using the null cover characterization, we can see that X is not algorithmically random, because for any n, X lies in the union Un of 2n intervals each of length 2-2n, and the intersection of the Un has measure 0.
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: randomness
« Reply #11 on: Feb 14th, 2008, 12:05am » |
 Quote Quote  Modify Modify
|
on Feb 13th, 2008, 4:03pm, Eigenray wrote:| Of course, for any sequence, there exists a function whose output is that sequence, but this function will almost always be non-computable. |
|
If you have a finite sequence, isn't it very very simple to plot a polynomial through all the points? (i.e such that the sequence is f(0), f(1), f(2) etc)
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: randomness
« Reply #12 on: Feb 14th, 2008, 2:01am » |
 Quote Quote  Modify Modify
|
It is not the data that is random, but the process that generates it. Once you generate a random sequence, it becomes just data. Even though it might be meaningless to you.
A truly random process generates all outcomes with equal probability. Getting Shakespeare's complete works is just as likely as any other outcome. It wouldn't be truly random if Shakespeare's works and other suspicious outcomes, like all zeros, would be excluded as "non-random". So no sequence is more random than another one. You cannot test randomness, just like if I give you a number between 1 and 6, you cannot tell whether I used a perfect die to generate it.
But, well, some data are suspicious. Some small subset of all possible outcomes can be explained by a simple non-random process. By declaring all these suspicious cases as "generated by a non-random process" and all others as "generated by a random process", you have a good probabiliy to be right ... provided you can recognize the simple process. Encrypted or compressed data can look very random, even though it usually is not.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: randomness
« Reply #13 on: Feb 14th, 2008, 5:04am » |
 Quote Quote  Modify Modify
|
on Feb 14th, 2008, 12:05am, towr wrote:
If you have a finite sequence, isn't it very very simple to plot a polynomial through all the points? (i.e such that the sequence is f(0), f(1), f(2) etc) |
|
Yes but almost all sequences are infinite 
Besides, randomness only makes sense in the limit. It doesn't make much sense to ask if a single number, or finite sequence of numbers, is random. Unless these numbers are real valued, but then you can think of them as infinite binary sequences. The binary expansion of any computable number would be non-algorithmically random, of course, but there are only countably many such numbers.
|
|
 IP Logged IP Logged |
|
|
|
pex
Uberpuzzler
    

Gender: 
Posts: 880
|
 |
Re: randomness
« Reply #14 on: Feb 14th, 2008, 5:24am » |
 Quote Quote  Modify Modify
|
In my opinion, randomness is a property of the process that generates a sequence of numbers, not of the numbers themselves. Thus, given a sequence of numbers (be it finite or infinite, even ignoring the problem of how one can be given an infinite sequence if there is no deterministic rule for generating it), there is no way to tell whether the numbers come from a random process or not - unless one is shown the generating mechanism, of course.
|
|
 IP Logged IP Logged |
|
|
|
Benny
Uberpuzzler
    

Gender: 
Posts: 1024
|
 |
Re: randomness
« Reply #15 on: Feb 14th, 2008, 11:57am » |
 Quote Quote  Modify Modify
|
Kolmogorov complexity remained more of a curiosity than a practical mathematical tool. Right?
|
|
 IP Logged IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
Benny
Uberpuzzler
    

Gender: 
Posts: 1024
|
 |
Re: randomness
« Reply #16 on: Feb 14th, 2008, 12:06pm » |
 Quote Quote  Modify Modify
|
Didn't Paul Vitanyi, an information theorist at the Centre for Mathematics and Computer Science and the University of Amsterdam, both in the Netherlands, and his long-time collaborator Ming Li at the University of Waterloo in Canada, make huge progress in using Kolmogorov complexity?
I am referring to the famous geometric problem set out in the first half of this century by the German mathematician Hans Heilbronn.
The problem being : If a number of pebbles (n) are placed inside a square and triangles are drawn between them, what arrangement of pebbles makes the smallest triangle as large as possible?
Didn't they show that the area of the smallest triangle is proportional to 1/n^3?
I've tried to search for their result on the net, but couldn't find it. Could anyone provide a link?
|
|
 IP Logged IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: randomness
« Reply #17 on: Feb 14th, 2008, 2:02pm » |
 Quote Quote  Modify Modify
|
I believe you're referring to the Heilbronn triangle problem. Note that the largest possible value for the area of the smallest triangle is > 1/(8n2), because taking a prime p between n and 2n, no three of the p points (x,x2) mod p are collinear.
What Vitanyi et al. showed is that if the points are chosen uniformly at random, then the expected area of the smallest triangle is bounded above and below by C/n3.
Here's the idea: Fix n, and an integer 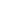 > 0. There are C(K2,n) ways to pick n points from a KxK grid. So most configurations X can't be described in much fewer than log C(K2,n) bits (log=log2). Specifically, at least the fraction (1-2- > 0. There are C(K2,n) ways to pick n points from a KxK grid. So most configurations X can't be described in much fewer than log C(K2,n) bits (log=log2). Specifically, at least the fraction (1-2-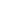 ) of them satisfy ) of them satisfy
(*) C(X|n,K)  log(C(K2,n)) - log(C(K2,n)) - 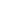 , ,
where C(X|n,K) is the length of the smallest program that outputs X given n,K. Call the configuration X incompressible if (*) holds.
Here's one way to describe a configuration X. Let PQR be the triangle of smallest area A, and suppose L=PQ is the longest side, and let H=2A/L. Then we can specify all points other than R in C(K2,n-1) ways, and then {P,Q} in C(n-1,2) ways. Let g be the gcd of the coordinates of Q-P. Then 2A = |(Q-P)x(Q-R)| is divisible by g, so HL = 2A = fg for an integer f. Specify this integer f with log(f) bits. This determines H. Now the point R lies on a line segment parallel to PQ, and a distance H from it. Since PQ was the longest side, the length of these segments are < PQ, and the two of them together have no more than 2g points. So finally we can specify R given an extra log(2g) bits. Since 2fg=4A, we therefore have
C(X|n,K)  log[C(K2,n-1)C(n-1,2)*4A] + c, log[C(K2,n-1)C(n-1,2)*4A] + c,
where c is an absolute constant (the length of a program which can reverse the steps in the above paragraph). Now we can combine the two inequalities to get that if X is incompressible, then
A/(K-1)2  2c-1- 2c-1-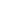 (K2-n-1)/(K-1)2 1/[n(n-1)(n-2)] (K2-n-1)/(K-1)2 1/[n(n-1)(n-2)]  c'/[2 c'/[2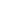 n3] n3]
for K sufficiently large, where c' is again an absolute constant. Since X is incompressible with probability at least (1-2-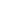 ), the lower bound on the expected value of the smallest area follows. ), the lower bound on the expected value of the smallest area follows.
For the upper bound, the idea is: if the area A of the smallest triangle is large, then any two points rule out a large area where there can be no third point. Then one can pick n/2 points such that, once specified, the other n/2 points lie in a small region, so they can be specified efficiently. If A is large enough, then this shows that X is compressible.
|
| « Last Edit: Feb 14th, 2008, 8:17pm by Eigenray » |
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: randomness
« Reply #18 on: Feb 14th, 2008, 4:49pm » |
 Quote Quote  Modify Modify
|
on Feb 13th, 2008, 10:45am, pex wrote:
Can we? I do not think so; we can never be completely sure that any given sequence is not the result of some random process. |
|
You lost the context ... two posts earlier I have said ... ... with high probability
|
|
 IP Logged IP Logged |
|
|
|
JiNbOtAk
Uberpuzzler
    

Hana Hana No Mi
Gender: 
Posts: 1187
|
 |
Re: randomness
« Reply #19 on: Feb 14th, 2008, 7:52pm » |
 Quote Quote  Modify Modify
|
on Feb 14th, 2008, 2:01am, Grimbal wrote:| Getting Shakespeare's complete works is just as likely as any other outcome. |
|
I was reminded of the time I was in my high school, we had an essay assignment ( of about 150 words ) to be completed. A really weird thing happened, when 2 of my classmates submitted an essay which was identical, even to the grammar mistakes ! The teacher of course, assumed that one guy copied from the other, but as one of them is my best friend, plus the fact he wrote out the essay together with me, independently, it was truly a weird experience. Even the guys who wrote it did not seem to understand how it came to be. So I guess, in selecting random words to form an essay ( from a select group ), there is a probability of 2 people choosing exactly the same 150 words.
|
|
 IP Logged IP Logged |
Quis custodiet ipsos custodes?
|
|
|
temporary
Full Member
  

Posts: 255
|
 |
Re: randomness
« Reply #20 on: Feb 14th, 2008, 8:41pm » |
 Quote Quote  Modify Modify
|
You can only have randomness in an infinite sequence without pattern or function, but you would need to see every one of the infinite numbers to know it is random.
|
|
 IP Logged IP Logged |
My goal is to find what my goal is, once I find what my goal is, my goal will be complete.
|
|
|
Christine
Full Member
  

Posts: 159
|
 |
Re: randomness
« Reply #21 on: Mar 3rd, 2008, 12:41am » |
 Quote Quote  Modify Modify
|
I don't understand the idea that a book is probably not a completely random string, that it can be compressed significantly. How could you compress it? I'm not really sure about this. Say you take Hamlet from Shakespeare. How could you compress it? you cannot create a small program that will be able to create all hamlet again, unless you actually write the text on the program. I've read the Infinite monkey theorem, see link http://en.wikipedia.org/wiki/Infinite_monkey_theorem
I guess I might be wrong or just confused about the whole thing, but I don't see how. What do you guys think?
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: randomness
« Reply #22 on: Mar 3rd, 2008, 1:04am » |
 Quote Quote  Modify Modify
|
on Mar 3rd, 2008, 12:41am, Christine wrote:| I don't understand the idea that a book is probably not a completely random string, that it can be compressed significantly. How could you compress it? I'm not really sure about this. Say you take Hamlet from Shakespeare. How could you compress it? you cannot create a small program that will be able to create all hamlet again, unless you actually write the text on the program. I've read the Infinite monkey theorem, see link http://en.wikipedia.org/wiki/Infinite_monkey_theorem |
|
Neverytheless, I wrote a program that did exactly that, compressing Hamlet to a fraction of its size. 
Consider what it means to not be random*: it means that there are significant patterns in the string. Take another example, consider you throw a coin 5 times, and they all come up heads. Now you can write HHHHH to describe it, or 5H, the latter is only 40% of the size, by exploiting the pattern.
In the case of a text like Hamlet, you can use the fact that most words repeat. So you can use a dictionary and replace them with a shorter index (which tells you which word in the dictionary it is).
Now, if you have a totally random string, then you can't have an algorithm that is guaranteed to compresses it, because there aren't enough shorter strings to uniquely identify strings of that size. But, texts are never random strings (otherwise we couldn't understand them), so they're compressible as long as you know in what way they aren't random. The more you know, the better you can compress them.
But the same algorithms that can compress texts well, would probably inflate random strings. Consider again a series of coinflips, HHTHT, using the same kind of encoding as before, we get 2H1T1H1T, 60% longer than before, rather than shorter. This is because the pattern we try to exploit simply isn't there in this case.
*) I'm using the colloquial sense of random here; as has been said, 'random' doesn't really apply to sequences but to the process that generates them. But some days it just doesn't pay to say "this sequence is, with very high likelihood, generated by a process that is significantly random" instead of "this sequence is random".
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Random Lack of Squiggily Lines
Senior Riddler
   

Everything before 7/1/2008 is now irrelevant.
Gender: 
Posts: 460
|
 |
Re: randomness
« Reply #23 on: Mar 3rd, 2008, 4:49pm » |
 Quote Quote  Modify Modify
|
But I AM the product of those monkeys.....
|
|
 IP Logged IP Logged |
You can only believe i what you can prove, and since you have nothing proven to cmpare to, you can believe in nothing.
I have ~50 posts to hack a "R" into a "D". Which one?
|
|
|
Benny
Uberpuzzler
    

Gender: 
Posts: 1024
|
 |
Re: randomness
« Reply #24 on: Mar 17th, 2008, 8:42am » |
 Quote Quote  Modify Modify
|
I need to go back to this thread if you don't mind. I'm considering doing some work with randomness.
Eigenray wrote,
"Note that the largest possible value for the area of the smallest triangle is > 1/(8n^2), because taking a prime p between n and 2n, no three of the p points (x,x^2) mod p are collinear."
I don't understand this. Could you please elaborate?
|
|
 IP Logged IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register