Author |
Topic: Designing a Pi Resistance (Read 3688 times) |
|
Barukh
Uberpuzzler
Gender: 
Posts: 2276
|
 |
Designing a Pi Resistance
« on: Nov 30th, 2007, 3:55am » |
 Quote  Modify
|
You are given an unlimited supply of unit (1 Ohm) resistors.
Devise an electrical circuit from a minimum number of unit resistors that has a resistance equal to  Ohms accurate to 8 decimal places.
|
|
 IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Designing a Pi Resistance
« Reply #1 on: Nov 30th, 2007, 4:35am » |
Quote Modify
|
Woud continued fractions help?
edit: here is a first try:
Code:--3-|-16-|--
|-1--|
|-1--|
|-1--|
|-1--|
|-1--|
|-1--|
|-1--|
|
|
Makes 355/113 = 3.1415929 with 26 resistors.
(numbers are resistors in series).
|
| « Last Edit: Nov 30th, 2007, 12:46pm by Grimbal » |
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Designing a Pi Resistance
« Reply #2 on: Nov 30th, 2007, 12:20pm » |
Quote Modify
|
on Nov 30th, 2007, 4:35am, Grimbal wrote:| Woud continuous fractions help? |
|
Nice guess! 
Quote:Makes 355/113 = 3.1415929 with 26 resistors.
(numbers are resistors in series). |
|
That's only 6 decimal places, right? I mean, after decimal point.
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Designing a Pi Resistance
« Reply #3 on: Nov 30th, 2007, 12:46pm » |
Quote Modify
|
I know, but the next item in the continued fraction is 292...
pi = [3, 7, 15, 1, 292, 1, 1, 1, 2, ...]
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Designing a Pi Resistance
« Reply #4 on: Nov 30th, 2007, 1:18pm » |
Quote Modify
|
And in the meantime, I know that a circuit as above, but where the 16 and 1's are replaced with other numbers can do it in 95 resistors.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Designing a Pi Resistance
« Reply #5 on: Dec 2nd, 2007, 6:05am » |
Quote Modify
|
on Nov 30th, 2007, 1:18pm, Grimbal wrote:| And in the meantime, I know that a circuit as above, but where the 16 and 1's are replaced with other numbers can do it in 95 resistors. |
|
|
|
IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 7527
|
|
Re: Designing a Pi Resistance
« Reply #6 on: Dec 2nd, 2007, 11:09am » |
Quote Modify
|
If you put in parallel:
29, 22, 11, 10, 8, 3, 3, 1, 1, 1, 1, 1, 1 ohm,
you get 0.141592658 ohm. And that takes 92 1-ohm resistors.
So add 3 at one end and you get pi ohm to 8 decimals.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Designing a Pi Resistance
« Reply #7 on: Dec 2nd, 2007, 2:43pm » |
Quote Modify
|
I think you can get 355/113 with only 15 resistors (that's what my program finds; unfortunately it doesn't say how it gets it yet). But it does offer potential for substantial improvement in general (assuming it's correct).
[edit]26 resistors seem to be enough to get 103993/33102; I'll need to work out how though  [/edit]
|
| « Last Edit: Dec 3rd, 2007, 3:10am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Designing a Pi Resistance
« Reply #8 on: Dec 3rd, 2007, 3:12am » |
Quote Modify
|
Beautiful solution, Grimbal!
The question is: is this the best possible circuit?
I think I've got an idea to approach this systematically, but need to think about this more.
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
Here's my proposal for 103993/33102 with 26 1-Ohm resistors
Note that this still needn't be the best circuit. Just the best of it's kind that realizes this fraction (if my algorithm didn't make mistakes, and if I didn't make a mistake drawing it out).
[edit]With equally many resistors, I can also get the next one, 104348/33215
And with 28,29,31,31,35,35 the next 6 fractions for pi respectively. Surprisingly few, I'd say.[/edit]
|
| « Last Edit: Dec 3rd, 2007, 4:31am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Designing a Pi Resistance
« Reply #10 on: Dec 4th, 2007, 9:23am » |
Quote Modify
|
Towr, I confirm your solution. Absolutely brilliant!
Is your algorithm based on integer factoring? What does it produce for the fraction 102928/32763?
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Designing a Pi Resistance
« Reply #11 on: Dec 4th, 2007, 9:42am » |
Quote Modify
|
on Dec 4th, 2007, 9:23am, Barukh wrote:Towr, I confirm your solution. Absolutely brilliant!
Is your algorithm based on integer factoring? |
|
Partly.
If we have two circuits which realize fraction a/b and c/d then by composing them in serial we get (ad+bc)/bd, and by composing them in parallel we get ac/(ad+bc). What my program does is to decompose a fraction x/y back into a,b,c,d and the recurse until we get the form x/1 or 1/y, picking the smallest among all decompositions each time (and storing intermediate results).
Quote:| What does it produce for the fraction 102928/32763? |
|
Also 26 resistors.
I'm still not sure it has to be the best circuit, though, because I don't really know if a circuit like
+-a-+--+
| d |
-+-b-+ +-
| e |
+-c-+--+ can be decomposed into a circuit of parallel and serial resistors.
|
| « Last Edit: Dec 4th, 2007, 9:43am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Designing a Pi Resistance
« Reply #12 on: Dec 4th, 2007, 10:04am » |
Quote Modify
|
Sure it can: since the node between a and d and the node between c and e are connected by the "output" wire they can be collapsed into one node, leading to a network with a || c || (b + (d || e)).
--SMQ
|
| « Last Edit: Dec 4th, 2007, 10:10am by SMQ » |
IP Logged |
--SMQ
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Designing a Pi Resistance
« Reply #13 on: Dec 4th, 2007, 10:12am » |
Quote Modify
|
Ah yes, I forgot a few resistors from my example.. (actually, the example I came across had even more, but those didn't contribute to my worries)
+-a-+-f-+
| d |
-+-b-+ +-
| e |
+-c-+-g-+
(Actually the original example is rather interesting, because it tries to arrive at an approximation of pi by using resistors of 1,2,3,..,10 ohms, at most once each)
|
| « Last Edit: Dec 4th, 2007, 10:14am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Designing a Pi Resistance
« Reply #14 on: Dec 4th, 2007, 10:45am » |
Quote Modify
|
Or even more simply:
---+-a-+-d-+
| c |
+-b-+-e-+---
Obviously networks like that can still be solved with KCL/KVL, but I don't think they have a simple series/parallel representation, no.
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Designing a Pi Resistance
« Reply #15 on: Dec 4th, 2007, 10:54am » |
Quote Modify
|
So might we have a smaller circuit that has such sub-circuits? Or is 26 the best?
Trying every possible circuit with 25 or less nodes seems a bit much work.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Designing a Pi Resistance
« Reply #16 on: Dec 5th, 2007, 11:06am » |
Quote Modify
|
I'm not sure if this approach can yield a computationally-workable search for a minimal network or not, but there's a relatively-simple method for solving general equal-valued resistor networks using KCL to generate a system of linear equations. Consider the following resistor network with eight equal-valued resistors connecting four nodes (labeled a, b, c and d):
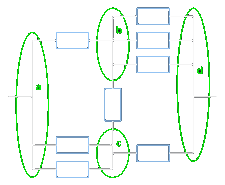
It can be represented by the following symmetric weighted adjacency matrix A, where the weights are the numbers of resistors connecting a pair of nodes (and therefore the reciprocals of the resistances between the nodes):
| | | a | b | c | d | | a | | | 0 | 1 | 2 | 0 | | b | | | 1 | 0 | 1 | 3 | | c | | | 2 | 1 | 0 | 1 | | d | | | 0 | 3 | 1 | 0 |
KCL states simply that, in a steady state, the net current entering any node is equal to the net current leaving that node. Let Ixy be the current from node x to node y, Rxy = 1 / Axy be the (direct, not equivalent) resistance between nodes x and y, and Vx be the voltage at node x with respect to some reference voltage. By Ohm's law, Ixy = (Vx - Vy) / Rxy = (Vx - Vy)Axy.
To use KCL to solve for the equivalent resistance of the network, we define voltages at the input node (a) and output node (d), then use KCL to generate a system of linear equations to solve for the voltages at the other nodes. Let Va = 1 and Vd = 0. By KCL we have:
Iab = Ibc + Ibd at node b and
Iac + Ibc = Icd at node c.
Substituting using the Ohm's law equation above gives:
(Va - Vb)Aab - (Vb - Vc)Abc - (Vb - Vd)Abd = 0
(Va - Vc)Aac + (Vb - Vc)Abc - (Vc - Vd)Acd = 0
Substituting Va = 1 and Vd = 0 and rearranging terms gives the following system of linear equations in Vb and Vc:
(Aab + Abc + Abd) Vb - Abc Vc = Aab
-Abc Vb + (Aac + Abc + Acd) Vc = Aac
This is a specific case of the general form in which there is an equation for each node with unknown voltage where, in the equation for node x, the coefficient of Vx is sum(Axy) for all y, the coefficient for every other Vy is -Axy, and the constant term on the right is Aax. (Since A is symmetric, Axy and Ayx can be used interchangeably.)
Solving the system of equations gives values of the unknown voltages. In our example, Vb = 6/19 and Vc = 11/19.
With the voltages at all nodes determined, the total current Inet through the network is just Aad + VbAbd + VcAcd (in general, if the last node is x, Inet = sum(VyAxy) for all y) -- 29/19 in our example.
Finally, from Ohm's law again, Requiv = (Va - Vd) / Inet = 1 / Inet = 19/29. This gives us a method for efficiently solving any symmetric weighted adjacency matrix for an equivalent resistance.
Now, what I'm thinking is thet there might be some dynamic/iterative approximation algorithm to work this process in reverse: given a target Requiv, a tolerance, and a number of nodes, find integer values for the elements of the adjacency matrix with the least sum.
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Designing a Pi Resistance
« Reply #17 on: Dec 5th, 2007, 1:41pm » |
Quote Modify
|
| |  | a1,n | 
| T | | 1 | 0 |  | 0 | 0 |
| -1 | | 1 |
| | |  | a2,n |
| | | -a2,1 |  a2,i | | -a2,n-2 | -a2,n-1 |
| | | 0 |
| | Requiv = 1 / | |  |
| | | | |  | | |
| | | |
| | | | an-2,n |
| | | -an-2,1 | -an-2,2 | | an-2,i | -an-2,n-1 |
| | | 0 |
| | |  | an-1,n | 
| | | -an-1,1 | -an-1,2 | | -an-1,n-2 | an-1,i |
| | | 0 |
|
--SMQ
|
| « Last Edit: Dec 6th, 2007, 5:14am by SMQ » |
IP Logged |
--SMQ
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print
Pi-circuit.pdf