 Author
Author |
Topic: try to solve this riddle (Read 3475 times) |
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
try to solve this riddle
« on: Sep 27th, 2007, 8:02pm » |
 Quote Quote  Modify Modify
|
Prove that uncountable infinity is higher than countable infinity. Linking to a page that says uncountable infinity is higher doesn't count.
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: try to solve this riddle
« Reply #1 on: Sep 27th, 2007, 8:57pm » |
 Quote Quote  Modify Modify
|
Should we use cardinals or robins?
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: try to solve this riddle
« Reply #2 on: Sep 27th, 2007, 9:35pm » |
 Quote Quote  Modify Modify
|
Let S be a set with uncountably many elements. Now suppose that the size of S is less than or equal to the size of the set of natural numbers, i.e. suppose that "uncountable infinity" is no bigger than "countable infinity". Then, by the definition of the terms, there is a one-to-one mapping from S to the natural numbers. Then there is a sequence of natural numbers n1, n2, n3,... such that the image of S in the natural numbers consists exactly of that sequence. But then S is countable, for we can order the elements of S by making first the element of S mapping to n1, second the element mapping to n2, etc. This contradicts the assumption that S is uncountable. So it is not the case that the size of S is less than or equal to the size of the set of natural numbers. Thus the size of S is bigger than countable infinity, i.e. "uncountable infinity" is bigger than countable infinity.
Of course, showing that an uncountable set (and therefore "uncountable infinity") exists is a very different (and more difficult) matter.
|
| « Last Edit: Sep 27th, 2007, 9:41pm by Obob » |
 IP Logged IP Logged |
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: try to solve this riddle
« Reply #3 on: Sep 28th, 2007, 7:21am » |
 Quote Quote  Modify Modify
|
True. Which is bigger, uncountable infinitycountable infinity or countable infinityuncountable infinity?
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: try to solve this riddle
« Reply #4 on: Sep 28th, 2007, 7:33am » |
 Quote Quote  Modify Modify
|
Which uncountable infinity?
Because, you know, there are more than one.
|
|
 IP Logged IP Logged |
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: try to solve this riddle
« Reply #5 on: Sep 28th, 2007, 8:16am » |
 Quote Quote  Modify Modify
|
Yes; your initial question was well defined because every uncountable set has more than countably many elements. This is why I put "uncountable infinity" in quotes in my initial post: uncountable infinity does not specify a precise "size."
Provided that in your follow up you have fixed a single set S with uncountably many elements, the second cardinal will be larger.
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: try to solve this riddle
« Reply #6 on: Sep 28th, 2007, 8:18am » |
 Quote Quote  Modify Modify
|
Well, let's see; assuming the axiom of choice:
Let  = =  0 and 0 and 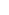 = =   , where , where 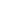 > 0. > 0.
Max( , 2 , 2 ) = 2 ) = 2     Max(2 Max(2 , 2 , 2 ) = 2 ) = 2    = 2 = 2 , ,
Max(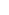 , 2 , 2 ) )  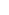   Max(2 Max(2 , 2 , 2 ) = 2 ) = 2  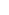   2 2 . .
    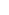   countable infinityuncountable infinity is at least as large as or larger than uncountable infinitycountable infinity. countable infinityuncountable infinity is at least as large as or larger than uncountable infinitycountable infinity.
Furthermore, since for all naturals (of which the cardinals are an extension) 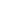 , ,  : : 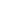  3, 3,   4, 4,  > > 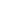 , we have that , we have that 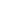  > >   , and since the normal arithmetic rules of exponentiation in naturals apply to cardinals as well, it would be reasonable to assume that countable infinityuncountable infinity is strictly larger than uncountable infinitycountable infinity -- but then reasonable assumptions tend to fail where transfinite cardinals are involved, so I'll stick with the weaker result. , and since the normal arithmetic rules of exponentiation in naturals apply to cardinals as well, it would be reasonable to assume that countable infinityuncountable infinity is strictly larger than uncountable infinitycountable infinity -- but then reasonable assumptions tend to fail where transfinite cardinals are involved, so I'll stick with the weaker result. 
on Sep 27th, 2007, 8:57pm, Michael_Dagg wrote:| Should we use cardinals or robins? |
|
Don't you mean orioles? 
--SMQ
|
| « Last Edit: Sep 28th, 2007, 8:21am by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: try to solve this riddle
« Reply #7 on: Sep 28th, 2007, 8:41am » |
 Quote Quote  Modify Modify
|
In fact, if w denotes the cardinality of the natural numbers and y denotes the cardinality of an uncountable set, then yw=y and wy=2y>y. So in fact wy is strictly larger.
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: try to solve this riddle
« Reply #8 on: Sep 28th, 2007, 6:10pm » |
 Quote Quote  Modify Modify
|
on Sep 28th, 2007, 8:18am, SMQ wrote:
Don't you mean orioles?  --SMQ --SMQ |
|
Yes, you are correct. I don't know what I was thinking!
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
srn437
Newbie


the dark lord rises again....
Posts: 1
|
 |
Re: try to solve this riddle
« Reply #9 on: Sep 28th, 2007, 7:43pm » |
 Quote Quote  Modify Modify
|
Correct. Is countable infinity a subset of uncountable infinity?
|
|
 IP Logged IP Logged |
|
|
|
Obob
Senior Riddler
   

Gender: 
Posts: 489
|
 |
Re: try to solve this riddle
« Reply #10 on: Sep 28th, 2007, 11:27pm » |
 Quote Quote  Modify Modify
|
Countable infinity and uncountable infinity aren't sets, so that question makes no sense.
An uncountably infinite set does have a countably infinite subset, however.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register