 Author
Author |
Topic: Pandigital expressions (Read 2440 times) |
|
Leo Broukhis
Senior Riddler
   

Gender: 
Posts: 459
|
 |
Pandigital expressions
« on: Sep 17th, 2007, 9:29pm » |
 Quote Quote  Modify Modify
|
What is the min positive integer that cannot be represented as an expression that uses only digits 1 to 9 - each one exactly once in any order, four arithmetic operations (+, -, *, /) and parentheses?
Concatenating digits is not allowed.
E.g.
1 = (3+5+7-2-9)/8*(6-4)*1
10 = 3*5*1+6-9+8+4-7*2
100 = 4*1+(2+7)*8+6+9*(5-3)
1000 = 8*(3+7)*(6+9-2*5/4/1)
10000 = (7*(((2+3)*9)*(5-1))-6-4) * 8
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Pandigital expressions
« Reply #1 on: Sep 18th, 2007, 8:27am » |
 Quote Quote  Modify Modify
|
I wouldn't try that without a computer.
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Pandigital expressions
« Reply #2 on: Sep 18th, 2007, 8:33am » |
 Quote Quote  Modify Modify
|
I'm working on trying it with a computer, but there are a huge number (tens of trillions) of legal expressions, with likely multiple billions of unique integer values (although integer values must be in the range of 1-9! to 9!). If I can find a fast way to eliminate expressions which are equivalent by commutation or associativity that might bring it into the realm of computational feasibility practicality on my hardware...
--SMQ
|
| « Last Edit: Sep 18th, 2007, 8:59am by SMQ » |
 IP Logged IP Logged |
--SMQ
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Pandigital expressions
« Reply #3 on: Sep 18th, 2007, 9:25am » |
 Quote Quote  Modify Modify
|
on Sep 18th, 2007, 8:33am, SMQ wrote:| (although integer values must be in the range of 1-9! to 9!). |
|
Or maybe 9!*3/2. 
|
|
 IP Logged IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
   

Gender: 
Posts: 459
|
 |
Re: Pandigital expressions
« Reply #4 on: Sep 18th, 2007, 10:04am » |
 Quote Quote  Modify Modify
|
Quote:
Exactly!
SMQ: I have not started writing such a program, but the base data structure should be the bitmask of used digits, the value, top arith op, and two links to the operands. This way all equivalences are automatically avoided.
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Pandigital expressions
« Reply #5 on: Sep 18th, 2007, 10:19am » |
 Quote Quote  Modify Modify
|
Actually, after some thought, I think I'm going to use common subexpression elimination "in reverse." Two subexpressions are unique iff they have different values or have the same values but utilize different terms. Given all all unique subexpressions of lengths 1 through n-1 it is fairly straightforward to calculate all subexpressions of length n, and by eliminating duplicate values early in the process the number of calculations is greatly reduced. Together with a few other tricks, I think that can be made to run in a reasonable amount of time.
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Pandigital expressions
« Reply #6 on: Sep 18th, 2007, 10:46am » |
 Quote Quote  Modify Modify
|
I've got a program (written for another thread long time ago). It's highly non-optimized - takes a long time to run!

|
|
 IP Logged IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
   

Gender: 
Posts: 459
|
 |
Re: Pandigital expressions
« Reply #7 on: Sep 18th, 2007, 11:11am » |
 Quote Quote  Modify Modify
|
Another interesting question: what is the expected value of such an expression (assuming all 4 arith ops are equiprobable, and omitting division by zero).
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Pandigital expressions
« Reply #8 on: Sep 19th, 2007, 2:18am » |
 Quote Quote  Modify Modify
|
Just for the record:
Digits Min non-rep
-----------------------------
1-5 76
1-6 284
1-7 1413
|
| « Last Edit: Sep 19th, 2007, 2:18am by Barukh » |
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Pandigital expressions
« Reply #10 on: Sep 19th, 2007, 2:37am » |
 Quote Quote  Modify Modify
|
It is not exactly the same. The Integer Sequence Encyclopedia includes zero, which could be used to cancel some terms. It doesn't seem to affect the result much, though.
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Pandigital expressions
« Reply #11 on: Sep 19th, 2007, 6:16am » |
 Quote Quote  Modify Modify
|
Also, the Sloanes sequence doesn't require you to use all the digits (see the example there). My program looks like it'll be reasonably fast, but it runs out of memory, so I have to rewrite parts of it to be able to store intermediate results to disk...
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Pandigital expressions
« Reply #12 on: Sep 19th, 2007, 6:51am » |
 Quote Quote  Modify Modify
|
SMQ, I think that restriction won't change the final result.
But computing the result in a reasonable amount of time is an interesting and non-trivial task in its own right. My naive program would compute it in more than 27 years on a single machine... 
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Pandigital expressions
« Reply #13 on: Sep 19th, 2007, 2:44pm » |
 Quote Quote  Modify Modify
|
I can now confirm that the smallest positive integer which cannot be represented as a pandigital expression is 38103 (matching the sequence from Sloanes). 
My program takes a bit over 1/2 hour (on a 3.2 GHz Pentium 4) to generate all unique integer values of pandigital expressions (there are 205901 of them). I'll work on the expected value question tomorrow. 
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Leo Broukhis
Senior Riddler
   

Gender: 
Posts: 459
|
 |
Re: Pandigital expressions
« Reply #14 on: Sep 19th, 2007, 3:16pm » |
 Quote Quote  Modify Modify
|
SMQ: Disallow division, and things should be much faster  This will let you answer the question what is the min number that really needs division, and how many of them out of 205901 do. This will let you answer the question what is the min number that really needs division, and how many of them out of 205901 do.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: Pandigital expressions
« Reply #15 on: Sep 20th, 2007, 6:49am » |
 Quote Quote  Modify Modify
|
Very impressive, SMQ! I would like to learn about your program more than you outlined in one the previous posts.
|
|
 IP Logged IP Logged |
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Pandigital expressions
« Reply #16 on: Sep 20th, 2007, 7:02am » |
 Quote Quote  Modify Modify
|
Hmm, so far I count the number of expressions as 9! 48(C714-C614). Which is of order around 1013.
So you must optimise the enumeration as you have limited time...
|
| « Last Edit: Sep 20th, 2007, 7:03am by Hippo » |
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Pandigital expressions
« Reply #17 on: Sep 20th, 2007, 7:30am » |
 Quote Quote  Modify Modify
|
on Sep 20th, 2007, 6:49am, Barukh wrote:| Very impressive, SMQ! I would like to learn about your program more than you outlined in one the previous posts. |
|
Thanks. 
The primary data structure is a 512-element array of sets of rationals in lowest terms (one set of rationals for each set of digits used). After populating the trivial sets for single-digit subexpressions, the main loop is as follows:
For each n from 2 through 9
For each set S of n digits
For each pair of (nonempty) sets of digits A, B, A  B = S, A B = S, A  B = B = 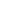
For each rational a in the set of rationals associated with A
For each rational b in the set of rationals associated with B
Add (iff not already present) to the set of rationals associated with S, each of:
a + b,
a - b,
b - a,
a * b,
a / b (iff b 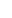 0), and 0), and
b / a (iff a 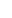 0). 0).
By keeping the sets of rationals in lowest terms, duplicate subexpression values are eliminated early in the process, bringing the number of calculations down by a factor of several thousand. To reach the 1/2 hour timeframe I additionally only consider integer results for n = 9, rather than deriving the entire set of unique rational results. The rest of the details are in caching large sets of rationals to disk in order to keep the RAM requirements reasonable for my platform (under 1GB).
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Pandigital expressions
« Reply #18 on: Sep 20th, 2007, 7:39am » |
 Quote Quote  Modify Modify
|
on Sep 20th, 2007, 7:02am, Hippo wrote:| Hmm, so far I count the number of expressions as 9! 48(C714-C614). Which is of order around 1013. |
|
You must be eliminating some obvious duplicates, as I get the number of lexicographically-distinct expressions as (17C8/17)  9! 9!  48 = 16C8 48 = 16C8  48. 48.
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Hippo
Uberpuzzler
    

Gender: 
Posts: 919
|
 |
Re: Pandigital expressions
« Reply #19 on: Sep 21st, 2007, 6:42am » |
 Quote Quote  Modify Modify
|
I enumerate all expresions in polish notation.
The hardest question was to count positions where can the operators be placed. (The 14C7-14C6 term).
BTW: I have thought about the algoritmn meanwhile ... I would use another set of 4 operations:
+/- as one of them, *, / , \ the others.
I would apply less complex expression to more complex therefore two kinds of division should be used /, \.
I would not store rational results if quotient is not multiple of not used numbers.
I would store results without sign with flag denoting if both signs are reachable.
If the same result is obtained for the given set of numbers, the flags are ored. (*,/,\ or's the flag's too, +/- ... the flag rules are more complicated but easy ... it generates two results, one with flag set (-), the other is ored flag of the originals (+))
Rest will be simillar algorithm to yours, but I will generate expressions in order of growing number of used numbers.
... I haven't start codding yet (and I am not sure I will).
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Pandigital expressions
« Reply #20 on: Sep 21st, 2007, 7:09am » |
 Quote Quote  Modify Modify
|
I thought that if I were to write the program, I would restrict the expressions to something like
expression = term ['+' term]* ['-' term]*
term = factor ['*' factor]* ['/' factor]*
factor = number | '(' expression ')'
where the terms and factors are in increasing order within each operation. As a result, for instance, I would not try A+B if B is already a sum or if A is the result of a subtraction. This way, I would not try the same sum in all possible permutations. But I later realized that SMQ's method of pairing intermediate results in all possible ways and checking whether the value exists already for the same set of digits is just as efficient to prune these cases. The only difference is that the result needs to be actually computed. So in the end, I don't think it would be much faster.
|
| « Last Edit: Sep 21st, 2007, 7:10am by Grimbal » |
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Pandigital expressions
« Reply #21 on: Sep 21st, 2007, 7:45am » |
 Quote Quote  Modify Modify
|
on Sep 21st, 2007, 6:42am, Hippo wrote:I enumerate all expresions in polish notation.
The hardest question was to count positions where can the operators be placed. (The 14C7-14C6 term). |
|
As did I, but I'm pretty sure that term should be Cat(8) (where Cat(n) is the nth Catalan Number) = 17C8/17 = 16C8 - 16C7 = 1430 rather than Cat(7) = 15C7/15 = 14C7 - 14C6 = 429.
My program to enumerate the complete set of result values, along with their multiplicities and an example expression, looks like it should finish sometime tomorrow (the relative slowness due mainly to my inefficient algorithm to merge partial results in memory with the 3GB+ file of results on disk). Then I'll be able to answer the expected value question. 
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 7527
|
 |
Re: Pandigital expressions
« Reply #22 on: Sep 21st, 2007, 8:28am » |
 Quote Quote  Modify Modify
|
I think that a mean value has no meaning unless you tell exactly what expression are considered as equal.
For instance, do "1-(2-3)", "(1-2)+3" and (3+1)-2 count as different expressions?
Co "(1+2)+3" and "1+(2+3)" count as the same?
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Pandigital expressions
« Reply #23 on: Sep 21st, 2007, 8:46am » |
 Quote Quote  Modify Modify
|
I would consider all of those distinct expressions, some of which have the same value as others. My reasoning being that when written in postfix notation or graphed as an operator tree they would have distinct representations. That's the definition of multiplicity my currently-running program is using. ... or would be if I had remembered to multiply by 2 for addition and multiplication, gol durn it!   Now I'm going to have to start it over. Maybe I can improve on the merge algorithm while I'm at it. Now I'm going to have to start it over. Maybe I can improve on the merge algorithm while I'm at it.
(That definition is useful in this case as the total number of distinct expressions is fairly easily calculated (although Hippo and I seem do disagree on which Catalan number to use) and can serve as a sanity check on the results of the program...)
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Leo Broukhis
Senior Riddler
   

Gender: 
Posts: 459
|
 |
Re: Pandigital expressions
« Reply #24 on: Sep 21st, 2007, 9:05am » |
 Quote Quote  Modify Modify
|
on Sep 21st, 2007, 6:42am, Hippo wrote:
I would not store rational results if quotient is not multiple of not used numbers.
|
|
And that would be your mistake. Note, for example, that 21 = 6 / (1 - 5/7)
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register