 Author
Author |
Topic: Card Game (Read 4932 times) |
|
spanchap
Newbie


Suresh
Gender: 
Posts: 40
|
Hello.
Thanks to all the contributors for the many excellent puzzles. I am a puzzle freak and have enjoyed solving these puzzles tremendously.
Here is my first contribution - I do not know if this puzzle or a variation has been posted in the past
I suggest the following game to you: I have a deck of 52 cards where the cards are well shuffled and random.
You get to pick a card. If it is red and you choose to pick no more cards, I pay you a dollar. If it is black and you choose to pick no more cards, you pay me a dollar.
You can continue picking additional cards from the deck till you choose to stop. When you choose to stop, I pay you the number of dollars equal to # of red cards picked minus # of black cards picked. If you ended up picking more black cards, you pay me the number of dollars equal to # of black cards picked minus # of red cards picked. If # of black cards picked = # of red cards picked, we call it even and go to a bar and have a quite drink. What is the expected value of this game for you? What should your strategy be?
- Suresh
|
| « Last Edit: Mar 23rd, 2007, 7:19am by spanchap » |
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Card Game
« Reply #1 on: Mar 23rd, 2007, 3:41am » |
 Quote Quote  Modify Modify
|
Is it a standard 52 cards deck, i.e. with exactly half of them red and half of them black?
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Card Game
« Reply #2 on: Mar 23rd, 2007, 3:44am » |
 Quote Quote  Modify Modify
|
At worst you'd gain nothing and lose nothing, because you can always go to the end of the deck.
The problem sounds somewhat familiar..
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
spanchap
Newbie


Suresh
Gender: 
Posts: 40
|
 |
Re: Card Game
« Reply #3 on: Mar 23rd, 2007, 7:20am » |
 Quote Quote  Modify Modify
|
It is a 52 card deck and yes, the value of the game is non zero as the worst you can do is to lose no money
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Card Game
« Reply #4 on: Mar 23rd, 2007, 10:47am » |
 Quote Quote  Modify Modify
|
I did a numerical simulation calculation in Ex... a well-known spreadsheet program. I get a value of 2.6245.
For each possible number of reds and blacks I average the values for the situation with one red or one black card less, weighted with the probability of each possibility. I stop if the offered value (red-black) is larger than the expected earning.
Roughly you should stop if you have 25% +1 more reds than blacks.
|
| « Last Edit: Mar 25th, 2007, 7:00am by Grimbal » |
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Card Game
« Reply #5 on: Mar 23rd, 2007, 12:52pm » |
 Quote Quote  Modify Modify
|
I agree with your expected value of the game, Grimbal, but not your characterization of the strategy -- near the beginning of the game you want to allow far more than 25% reds. For instance, if you start out drawing all reds, you don't want to stop until you have 6 reds and no blacks...
Empirically, one formula I found is that you want to stop iff your current score > (1/2) * (number of remaining cards)0.618. I don't know if that 1/ (where (where  is the golden ratio) in the exponent is a coincidence or not... is the golden ratio) in the exponent is a coincidence or not...
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
spanchap
Newbie


Suresh
Gender: 
Posts: 40
|
 |
Re: Card Game
« Reply #6 on: Mar 23rd, 2007, 1:00pm » |
 Quote Quote  Modify Modify
|
The process used by Grimbal to calculate the expected value can also be used to find the optimum strategy. Essentially you can find the expected value of the game with r red cards left and b black cards left. You continue playing the game if the expected value of the game with the remaining cards is positive.
|
|
 IP Logged IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Card Game
« Reply #7 on: Mar 23rd, 2007, 1:43pm » |
 Quote Quote  Modify Modify
|
Indeed, but I was phrasing the strategy in terms of the question: "if there are N cards remaining, what split of red and black cards gives a positive expected value?" And the empirical answer I found was: the expected value of a game of N cards is positive if and only if the number of black cards minus the number of red cards (i.e. the number of extra red cards you're already holding) is less than approximately (1/2)N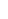 where where  = =  -1 -- a somewhat surprising formula given its apparent inclusion of the Golden Ratio -- a value which doesn't often appear in statistical formulas. -1 -- a somewhat surprising formula given its apparent inclusion of the Golden Ratio -- a value which doesn't often appear in statistical formulas.
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
Random Lack of Squiggily Lines
Senior Riddler
   

Everything before 7/1/2008 is now irrelevant.
Gender: 
Posts: 460
|
 |
Re: Card Game
« Reply #8 on: Mar 23rd, 2007, 3:47pm » |
 Quote Quote  Modify Modify
|
smq, how did you get the symbols on your post, i know you have to use ALT
|
|
 IP Logged IP Logged |
You can only believe i what you can prove, and since you have nothing proven to cmpare to, you can believe in nothing.
I have ~50 posts to hack a "R" into a "D". Which one?
|
|
|
Random Lack of Squiggily Lines
Senior Riddler
   

Everything before 7/1/2008 is now irrelevant.
Gender: 
Posts: 460
|
 |
Re: Card Game
« Reply #9 on: Mar 23rd, 2007, 3:48pm » |
 Quote Quote  Modify Modify
|
as soon as you have more red than black pay out, and if that never happens just go to the end of the deck.
|
|
 IP Logged IP Logged |
You can only believe i what you can prove, and since you have nothing proven to cmpare to, you can believe in nothing.
I have ~50 posts to hack a "R" into a "D". Which one?
|
|
|
spanchap
Newbie


Suresh
Gender: 
Posts: 40
|
 |
Re: Card Game
« Reply #10 on: Mar 23rd, 2007, 4:00pm » |
 Quote Quote  Modify Modify
|
tiber13,
Even if you are ahead by 1 ( 1 red more than black), you would want to continue the game if the expected value of playing a new game with the remaining cards is positive
|
|
 IP Logged IP Logged |
|
|
|
spanchap
Newbie


Suresh
Gender: 
Posts: 40
|
 |
Re: Card Game
« Reply #11 on: Mar 23rd, 2007, 4:22pm » |
 Quote Quote  Modify Modify
|
Grimbal,
Apart from running simulations, one could also derive the expected value as follows:
Expected value of game with R red cards and B blue cards = E(R,B) = Max(0, Probability of choosing R red cards from R+B cards times (E(R-1,B) + 1)) + Probability of choosing B black cards from R+B cards times (E(R,B-1) + 1)) )
Therfore E(R,B) = MAX (0, R/R+B * (E(R-1,B) + 1) + B/B+R * (E(R,B-1) -1))
Setting E(0,0) = 0, E(1,0) = 1 and E(0,1) = 0 and iterating for higher values of R and B results in E(26,26) = 2.6244755
|
|
 IP Logged IP Logged |
|
|
|
SWF
Uberpuzzler
    

Posts: 879
|
 |
Re: Card Game
« Reply #12 on: Mar 23rd, 2007, 6:21pm » |
 Quote Quote  Modify Modify
|
Perhaps towr is thinking of this similar question:
"A deck of 26 red and 26 black cards is shuffled into random order and placed face down. Then the cards are turned up one by one and observed by a guesser. He gets one guess: At a moment of his choice he may assert that the next card will turn up red. After this card is turned up the game ends and he wins if his assertion was correct, loses otherwise. And if he doesn't guess at all by the time all cards have been dealt, he loses by default. What guessing policy chosen in advance maximizes his chance of winning?"
Here is a link to thread discussing it.
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Card Game
« Reply #13 on: Mar 23rd, 2007, 8:04pm » |
 Quote Quote  Modify Modify
|
on Mar 23rd, 2007, 3:47pm, tiber13 wrote:| smq, how did you get the symbols on your post, i know you have to use ALT |
|
There are a number of ways of putting symbols in that are not universal, so if you use them, some part of your audience will not be able to see what you've done. Instead, they will see a meaningless string of characters. The ALT method you are thinking of is one of these methods.
There is, however, a method in this forum that is universal, since it makes use of gif images to produce the symbols. Exactly how has undergone several alterations, but the current method - due to SMQ - is explained in this thread.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
If there are n={1,2,3,...} cards left, then in order to keep playing, the number of red cards left should be at least
R = {1, 1, 2, 2, 2, 3, 3, 4, 4, 4, 5, 5, 6, 6, 7, 7, 8, 8, 8, 9, ...}.
In the first 10000 terms, every positive integer appears exactly twice, except for the numbers
A = {2, 4, 8, 13, 19, 27, 37, 47, 60, 73, 88, 105, 123, 142, 163, 185, 209, 234, 260, 288, 317, 348, 380, 413, 448, 485, 522, 562, 602, 644, 688, 733, 779, 826, 876, 926, 978, 1031, 1086, 1142, 1200, 1259, 1319, 1381, 1445, 1509, 1575, 1643, 1712, 1782, 1854, 1927, 2002, 2078, 2155, 2234, 2315, 2396, 2479, 2564, 2650, 2737, 2826, 2916, 3008, 3101, 3195, 3291, 3389, 3487, 3587, 3689, 3792, 3896, 4002, 4109, 4218, 4328, 4440, 4552, 4667, 4783, 4900},
which all appear three times each. The above list actually contains all the information you need to play the game with less than 10,000 cards. And for a standard deck, you only need to know the first five numbers.
For example, suppose there are 100 red cards left. Since there are 11 numbers  100 in the above list, you should keep playing as long as there are 100 in the above list, you should keep playing as long as there are  2*100+11 cards remaining. 2*100+11 cards remaining.
Doing a log-log fit on the last 50 entries, log A[x] ~ 1.995 log x - 0.317, so A[x] is apparently quadratic: A[x] ~ .709 x2 + 0.180 x + 0.730.
So A contains ~ sqrt(r/.709) numbers less than r, and if there are r red cards left, there should be no more than n ~ 2r + (r/.709)1/2 cards left to keep playing. Solving for r, if there are n cards left, there should be at least r ~ n/2 - (n/(8*.709))1/2 red cards left, which means
n - 2r ~ (.840 n)1/2
is the asymptotic threshold, agreeing with the analysis here (but disagreeing with SMQ).
Attached is a plot of f(n) = n - 2R[n], as a function of n, where R[n], as above, is the smallest r for which it is worth playing when there are r red cards left (out of n). For the most part, R[n+1] is alternately R[n] or R[n]+1, so f(n+1) is alternately f(n)+1 or f(n)-1, respectively; but when R[n+2]=R[n] (so R[n]  A), we have f(n+2) = f(n)+2. That is, f(n) mostly alternates up 1, down 1, but occasionally (~1/sqrt(n) of the time) goes up twice in a row, so at this resolution, the plot appears to consist of horizontal bars, bounded on either side by those n for which R[n] A), we have f(n+2) = f(n)+2. That is, f(n) mostly alternates up 1, down 1, but occasionally (~1/sqrt(n) of the time) goes up twice in a row, so at this resolution, the plot appears to consist of horizontal bars, bounded on either side by those n for which R[n]  A. A.
In red is the best <1, sqrt(n)>-fit through the last 50 "middle" points (n, f(n)) -- those for which R[n-1]=R[n+1]  A -- given by f(n) ~ 0.840 sqrt(n) - 1.493. (For clarity, only n<1000 is shown.) A -- given by f(n) ~ 0.840 sqrt(n) - 1.493. (For clarity, only n<1000 is shown.)
|
|
 IP Logged IP Logged |

|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Card Game
« Reply #15 on: Mar 25th, 2007, 7:06am » |
 Quote Quote  Modify Modify
|
on Mar 23rd, 2007, 12:52pm, SMQ wrote:| I agree with your expected value of the game, Grimbal, but not your characterization of the strategy -- near the beginning of the game you want to allow far more than 25% reds. For instance, if you start out drawing all reds, you don't want to stop until you have 6 reds and no blacks... |
|
Yep, I said "roughly". The optimal limit is at +/- 1 card.
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: Card Game
« Reply #16 on: Mar 25th, 2007, 7:09am » |
 Quote Quote  Modify Modify
|
on Mar 23rd, 2007, 4:22pm, spanchap wrote:Grimbal,
Apart from running simulations, one could also derive the expected value as follows:
|
|
I should have said "calculation". My formulas look much like the one you give. Probably they are a variation.
|
|
 IP Logged IP Logged |
|
|
|
Benny
Uberpuzzler
    

Gender: 
Posts: 1024
|
 |
Re: Card Game
« Reply #17 on: May 11th, 2008, 12:27pm » |
 Quote Quote  Modify Modify
|
A new problem:
When playing a game of blackjack, what are the odds that you will be dealt BlackJack on the first deal?
Assume you are playing with one opponent and your opponent is the dealer.
10, Jack, Queen, King are worth 10.
Aces are worth 11.
There's only one deck of cards being dealt.
To get a BlackJack (a natural), you need an ace and a card that is worth 10.
|
|
 IP Logged IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Card Game
« Reply #18 on: May 11th, 2008, 12:48pm » |
 Quote Quote  Modify Modify
|
Either you get the 10/J/Q/K first and then the A, or first the A and then 10/J/Q/K
So, 2* 4/13 * 1/13 = 8/169
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Benny
Uberpuzzler
    

Gender: 
Posts: 1024
|
 |
Re: Card Game
« Reply #19 on: May 11th, 2008, 1:45pm » |
 Quote Quote  Modify Modify
|
Perhaps i'm missing something here. This is how i see it:
First:
There are 16 ways to get a face card or 10. And there are 4 ways to get an ace. So there are 16*4 ways to get blackjack this way.
Second:
There are 52 cards in the deck,
so, there are 52 ways to draw the first card
then the dealer gets his first card,
then you're dealt w/ your second card
and 50 ways to draw the second.
so, 52*50 (number of ways)
The probability of getting blackjack is then:
(number of ways to get blackjack) / 52*50 = p
This gives a probability, and change that to odds.
|
|
 IP Logged IP Logged |
If we want to understand our world — or how to change it — we must first understand the rational choices that shape it.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: Card Game
« Reply #20 on: May 11th, 2008, 2:02pm » |
 Quote Quote  Modify Modify
|
It doesn't matter whether a card is in the dealer's hand or in the stack.
But I did make a mistake, it should be
16/52*4/51 + 4/52*16/51 = 32/663
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
temporary
Full Member
  

Posts: 255
|
 |
Re: Card Game
« Reply #21 on: May 13th, 2008, 7:14pm » |
 Quote Quote  Modify Modify
|
Do I not get to see the card until I stop or what, because if I do it is too easy to win(or in the worst case, draw)? The expected payoff(assuming I see the cards and play optimally) is 13.
|
|
 IP Logged IP Logged |
My goal is to find what my goal is, once I find what my goal is, my goal will be complete.
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
    

The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
 |
Re: Card Game
« Reply #22 on: May 13th, 2008, 7:38pm » |
 Quote Quote  Modify Modify
|
on May 13th, 2008, 7:14pm, temporary wrote:| Do I not get to see the card until I stop or what, because if I do it is too easy to win(or in the worst case, draw)? The expected payoff(assuming I see the cards and play optimally) is 13. |
|
It asked for the expected value of the game, not your age. 
|
|
 IP Logged IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
JiNbOtAk
Uberpuzzler
    

Hana Hana No Mi
Gender: 
Posts: 1187
|
 |
Re: Card Game
« Reply #23 on: May 14th, 2008, 4:44am » |
 Quote Quote  Modify Modify
|
on Mar 23rd, 2007, 12:52pm, SMQ wrote:I don't know if that 1/ (where (where  is the golden ratio) in the exponent is a coincidence or not... is the golden ratio) in the exponent is a coincidence or not... |
|
Very interesting SMQ. Anyone has any idea why ? And does it only work for 52 cards deck ? What if we had an 80 cards deck ( Assuming 20 cards for each suit ) ?
|
|
 IP Logged IP Logged |
Quis custodiet ipsos custodes?
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 2084
|
 |
Re: Card Game
« Reply #24 on: May 14th, 2008, 5:26am » |
 Quote Quote  Modify Modify
|
on May 14th, 2008, 4:44am, JiNbOtAk wrote:| Very interesting SMQ. Anyone has any idea why ? And does it only work for 52 cards deck ? What if we had an 80 cards deck ( Assuming 20 cards for each suit ) ? |
|
Eigenray's analysis above (with the graph) is much more thorough than mine and shows that the apparent  is just an illusion. is just an illusion.
--SMQ
|
|
 IP Logged IP Logged |
--SMQ
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register