 Author
Author |
Topic: 10 Prisoners and hats (Read 29271 times) |
|
irrational
Junior Member
 

Gender: 
Posts: 52
|
 |
10 Prisoners and hats
« on: Sep 19th, 2006, 9:20am » |
 Quote Quote  Modify Modify
|
10 straight-jacketed prisoners are on death row. Tomorrow they will be arranged in single file, all facing one direction. The guy in the front of the line (he can't see anything in front of him) will be called the 1st guy, and the guy in the back of the line (he can see the heads of the other nine people) will be called the 10th guy. An executioner will then put a hat on everyone's head; the hat will either be black or white, totally random. Prisoners cannot see the color of their own hat. The executioner then goes to the 10th guy and asks him what color hat he is wearing; the prisoner can respond with either "black" or "white". If what he says matches the color of the hat he's wearing, he will live. Else, he dies. The executioner then proceeds to the 9th guy, and asks the same question, then asks the 8th guy ... this continues until all of the prisoners have been queried.
This is the night before the execution. The prisoners are allowed to get together to discuss a plan for maximizing the number of lives saved tomorrow. What is the optimal plan?
My apologies if this has already been posted.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: 10 Prisoners and hats
« Reply #1 on: Sep 19th, 2006, 9:36am » |
 Quote Quote  Modify Modify
|
This problem is on the riddles' page.
The links are here.
|
|
 IP Logged IP Logged |
|
|
|
alien
Guest

|
 |
Re: 10 Prisoners and hats
« Reply #2 on: Sep 21st, 2006, 1:08pm » |
 Quote Quote  Modify Modify
 Remove Remove
|
It took me a week to solve this one on my own.  And a headache. And a headache. 
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: 10 Prisoners and hats
« Reply #3 on: Sep 22nd, 2006, 10:53am » |
 Quote Quote  Modify Modify
|
So what happens when the guy at the back has a grudge against the 9th guy?
|
|
 IP Logged IP Logged |
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: 10 Prisoners and hats
« Reply #4 on: Sep 25th, 2006, 4:09am » |
 Quote Quote  Modify Modify
|
Then he switches color.
Either that saves him and he can plead legitimate defense for killing his pal, or the switch kills him, in that case the bad guy gets killed by his own deeds. In both cases the story suits Hollywood moral standards.
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 10 Prisoners and hats
« Reply #5 on: Sep 25th, 2006, 3:26pm » |
 Quote Quote  Modify Modify
|
But what happens to everyone else?
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: 10 Prisoners and hats
« Reply #6 on: Sep 26th, 2006, 12:38am » |
 Quote Quote  Modify Modify
|
on Sep 25th, 2006, 3:26pm, Icarus wrote:| But what happens to everyone else? |
|
I'd say the 9th guy dies, the rest lives.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: 10 Prisoners and hats
« Reply #7 on: Sep 26th, 2006, 7:21am » |
 Quote Quote  Modify Modify
|
on Sep 26th, 2006, 12:38am, towr wrote:
I'd say the 9th guy dies, the rest lives.
|
|
But what if the 9th guy doesn't trust the 10th guy?
|
|
 IP Logged IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
    

Some people are average, some are just mean.
Gender: 
Posts: 13730
|
 |
Re: 10 Prisoners and hats
« Reply #8 on: Sep 26th, 2006, 7:58am » |
 Quote Quote  Modify Modify
|
on Sep 26th, 2006, 7:21am, rmsgrey wrote:| But what if the 9th guy doesn't trust the 10th guy? |
|
Well, if no one trusts anyone, it's 50-50 chances allround.
|
|
 IP Logged IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Grimbal
wu::riddles Moderator
Uberpuzzler
    

I am sorry Dave, I *can* do that.
Gender: 
Posts: 7528
|
 |
Re: 10 Prisoners and hats
« Reply #9 on: Sep 26th, 2006, 7:59am » |
 Quote Quote  Modify Modify
|
Yes, what if the 9th guy suspects the 10th guy would try something bad?
And What if the 7th guy trusts the 10th guy but believes the 9th guy is paranoid about the 10th, and feels the 8th guy is suicidal?
|
|
 IP Logged IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    

    
Gender: 
Posts: 2874
|
 |
Re: 10 Prisoners and hats
« Reply #10 on: Sep 28th, 2006, 5:39pm » |
 Quote Quote  Modify Modify
|
My preferred version with prisoners is for the successes and failures to be announced during the process, and then N prisoners to be shot at random (where N is the number of wrong "guesses") - that way, every (non-suicidal) prisoner has an incentive to follow the system.
Suicidal prisoners are easier to accomodate under a scheme where only the prisoner(s) guessing wrong get(s) killed, but the correct colour of each hat is announced immediately after the guess - they can then self-terminate without taking anyone else with them.
In fact, if the correct colour is announced after each guess, then only the first prisoner to speak needs to be reliable when each controls their own fate, but lacks incentive; when the penalties/rewards are shared, then everyone has incentive, but any unreliable prisoner can mess things up.
My preferred formulation overall is for a gameshow, where a number of contestants play the game, the pot increases for each correct answer, and then all participants split the pot.
|
|
 IP Logged IP Logged |
|
|
|
grungy
Newbie


Posts: 20
|
 |
Re: 10 Prisoners and hats
« Reply #11 on: Dec 9th, 2006, 2:50am » |
 Quote Quote  Modify Modify
|
If all the people are smart enough to understand this plan - it will even out to be a 95% success rate.
First of all, the guy at the back will see 9 hats. If he sees an odd amount of black hats, he will say black, if he sees an odd amount of white hats, he will say white. He is the only person who can die - and he has a 50% chance of survival anyway.
Then, say if the guy at the back says black, then it is the 9th person's turn. If he sees an odd number of black hats, he will know that his hat must be a white one. He will say white.
Then, the person ahead, knowing that since the other person said white, there must still be an odd number of black hats ahead. If the 8th person sees an even amount of black hats, he will know that his is white.
Then, this will continue all the way to the 1st person.
|
|
 IP Logged IP Logged |
|
|
|
Whiskey Tango Foxtrot
Uberpuzzler
    

Sorry Goose, it's time to buzz a tower.

Gender: 
Posts: 1672
|
 |
Re: 10 Prisoners and hats
« Reply #12 on: Dec 9th, 2006, 8:32am » |
 Quote Quote  Modify Modify
|
If you notice the link in the second post, you'll see that this is indeed the answer. I'm curious, though. What can be done if there are 30 prisoners (to round it off) and 3 different hat colors? What if there are 40 prisoners and 4 different hat colors?
|
|
 IP Logged IP Logged |
"I do not feel obliged to believe that the same God who has endowed us with sense, reason, and intellect has intended us to forgo their use." - Galileo Galilei
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 10 Prisoners and hats
« Reply #13 on: Dec 9th, 2006, 9:49am » |
 Quote Quote  Modify Modify
|
The first guy's chances get smaller, but everyone else can still be saved.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Whiskey Tango Foxtrot
Uberpuzzler
    

Sorry Goose, it's time to buzz a tower.

Gender: 
Posts: 1672
|
 |
Re: 10 Prisoners and hats
« Reply #14 on: Dec 9th, 2006, 10:13am » |
 Quote Quote  Modify Modify
|
What would the process be for that? What would the first guy saying red, blue, or yellow mean?
|
|
 IP Logged IP Logged |
"I do not feel obliged to believe that the same God who has endowed us with sense, reason, and intellect has intended us to forgo their use." - Galileo Galilei
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 10 Prisoners and hats
« Reply #15 on: Dec 9th, 2006, 12:52pm » |
 Quote Quote  Modify Modify
|
on Dec 9th, 2006, 10:13am, Whiskey Tango Foxtrot wrote:| What would the process be for that? What would the first guy saying red, blue, or yellow mean? |
|
The 2-color riddle uses mod-2 logic...
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Uwygoda
Newbie



Gender: 
Posts: 3
|
 |
Re: 10 Prisoners and hats
« Reply #16 on: Apr 7th, 2007, 1:56pm » |
 Quote Quote  Modify Modify
|
This riddle can be made much more interesting:
The basic problem stays the same, but this time there are an infinite (but enumerable) number of prisoners, and an infinite (but enumerable) number of hat colors. the solution assumes the Axiom of Choice (though non-mathematicians need not care about this fine point).
good luck to all.
anybody who wants the solution can email me.
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 10 Prisoners and hats
« Reply #17 on: Apr 7th, 2007, 3:05pm » |
 Quote Quote  Modify Modify
|
If we are limiting ourselves to denumerable sets, then there is no need for the Axiom of Choice, as the natural numbers are well-ordered even without it. It is only when you are dealing with larger sets that the A.C. is required.
|
| « Last Edit: Apr 7th, 2007, 3:07pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
iyerkri
Newbie


 
Gender: 
Posts: 17
|
 |
Re: 10 Prisoners and hats
« Reply #18 on: Apr 7th, 2007, 10:29pm » |
 Quote Quote  Modify Modify
|
on Dec 9th, 2006, 9:49am, Icarus wrote:| The first guy's chances get smaller, but everyone else can still be saved. |
|
In the n-color riddle, I think n-1 prisoners' fate have to sacrificed to luck, in order to save the rest. Using mod-n logic will still leave doubts in the second guy's mind, if n > 2. But, he can trust luck and save the others.
|
|
 IP Logged IP Logged |
|
|
|
Uwygoda
Newbie



Gender: 
Posts: 3
|
 |
Re: 10 Prisoners and hats
« Reply #19 on: Apr 7th, 2007, 11:57pm » |
 Quote Quote  Modify Modify
|
The solution I know to the denumerable version of the problem actually does require the A.C., even though natural numbers are well-ordered even without it.
If someone knows another solution which doesn't require it, I'd be glad to know.
|
|
 IP Logged IP Logged |
|
|
|
Barukh
Uberpuzzler
    

Gender: 
Posts: 2276
|
 |
Re: 10 Prisoners and hats
« Reply #20 on: Apr 8th, 2007, 4:37am » |
 Quote Quote  Modify Modify
|
on Apr 7th, 2007, 11:57pm, Uwygoda wrote:The solution I know to the denumerable version of the problem actually does require the A.C., even though natural numbers are well-ordered even without it.
If someone knows another solution which doesn't require it, I'd be glad to know. |
|
Maybe you will find this relevant.
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 10 Prisoners and hats
« Reply #21 on: Apr 8th, 2007, 5:21pm » |
 Quote Quote  Modify Modify
|
Uwygoda is correct about it requiring the Axiom of Choice. I was too glib in my assessment (something I realized at the time, but didn't let it stop me). After all, while 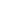 can be well-ordered without the axiom of Choice, can be well-ordered without the axiom of Choice, 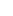 ( (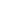 ) cannot be (at least this is my understanding - if it could be, then you could construct unmeasurable sets without A.C., and I've heard that this is impossible). ) cannot be (at least this is my understanding - if it could be, then you could construct unmeasurable sets without A.C., and I've heard that this is impossible).
I think that if you could make the needed choices here without A.C., you could also well-order 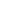 . .
Barukh's link brings up a side question of interest to me: Was this puzzle Eigenray's invention, or did he also get it from someplace else? I am curious about this because I have seen certain other puzzles that were invented by members of this forum (Eric Yeh in particular) and first published here make their way around other venues, and even find their way back here as newer members repost them - unaware of their origin. "Gods of Gibberland" is a particular example.
Is this another one?
|
| « Last Edit: Apr 8th, 2007, 5:29pm by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: 10 Prisoners and hats
« Reply #22 on: Apr 8th, 2007, 8:19pm » |
 Quote Quote  Modify Modify
|
on Apr 8th, 2007, 5:21pm, Icarus wrote:| Was this puzzle Eigenray's invention, or did he also get it from someplace else? |
|
I heard it from someone else, and I don't think it was original with him (although he noticed the connection to diamond himself).
I hadn't considered the case of more than one hat color, but it looks like for any ordinality of prisoners, and any set of hat colors, the prisoners can still save all but the first.
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: 10 Prisoners and hats
« Reply #23 on: Apr 8th, 2007, 9:52pm » |
 Quote Quote  Modify Modify
|
Yes. Deedlit's solution only needs minor modification to work for any number of hat colors. Specifically, if we can consider the hat colors to be values in some additive group G, then the first prisoner adds up the differences between the actual sequence and the representative sequence to obtain his value.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: 10 Prisoners and hats
« Reply #24 on: Apr 8th, 2007, 10:32pm » |
 Quote Quote  Modify Modify
|
That's cleaner than what I was thinking (e.g., if there are infinitely many prisoners, and an infinite set of hats H, they would agree on a bijection of H with the set of all finite strings from H).
But if you just say that they can find a group of any given cardinality, then the strategy is independent of whether there are infinitely many prisoners or hats.
|
|
 IP Logged IP Logged |
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register