Author |
Topic: Non-integer colouring (Read 7341 times) |
|
JocK
Uberpuzzler
Gender: 
Posts: 877
|
 |
Non-integer colouring
« on: May 24th, 2006, 2:55pm » |
 Quote  Modify
|
(Inspired by http://www.ocf.berkeley.edu/~wwu/cgi-bin/yabb/YaBB.cgi?board=riddles_med ium;action=display;num=1148278845)
Imagine an infinite square grid of points. The distance between nearest neighbour points is unity. And imagine that you are provided with an unlimited supply of 'anti-Diophantine markers'. If you place such a marker at a certain gridpoint, that gridpoint as well as all gridpoints that are a non-integer distance away from the marker get coloured.
Question 1: if you can place the markers at any gridpoint, how many markers do you need to colour the whole grid?
Question 2: if you are constraint to place the markers [edit]on gridpoints[/edit] such that their mutual distances are all integer, how many markers do you need to colour the whole grid?
|
| « Last Edit: May 27th, 2006, 11:57am by JocK » |
 IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Non-integer colouring
« Reply #1 on: May 24th, 2006, 6:41pm » |
Quote Modify
|
Well, let's start with the obvious. 
In one dimension, you need aleph-null markers either way: one covering each integer.
In two dimensions, the points left uncovered by a marker at (0,0) are exactly the legs of the pythagorean triples.
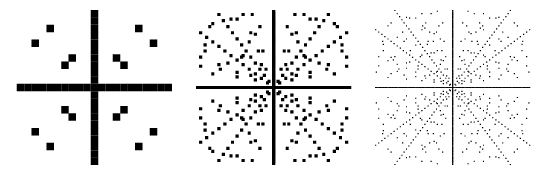
(image credit: Mathworld)
So far, that's all I have. 
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Non-integer colouring
« Reply #2 on: May 25th, 2006, 1:13am » |
Quote Modify
|
Interesting...
I think 2 markers placed at points (0, 0) and (-1, -1) will suffice. All we need is to show that the following system of Diophantine equations has no solutions:
x2 + y2 = m2,
(x+1)2 + (y+1)2 = n2
Indeed, subtracting the first from the second, we get:
2(x+y+1) = n2 - m2,
which means n-m >= 2. Therefore, 2(x+y+1) >= 4m+4, or x+y >= 2m+1. This is a contradiction, since x < m and y < m.
Even simpler: two markers (0, 0), (-1, 0) satisfy the conditions of the second question.
Makes sense?
|
| « Last Edit: May 25th, 2006, 3:36am by Barukh » |
IP Logged |
|
|
|
Sjoerd Job Postmus
Full Member
Posts: 228
|
|
Re: Non-integer colouring
« Reply #3 on: May 25th, 2006, 3:49am » |
Quote Modify
|
on May 25th, 2006, 1:13am, Barukh wrote:Even simpler: two markers (0, 0), (-1, 0) satisfy the conditions of the second question.
Makes sense?
|
|
(0,0), (-1,0):
Is (-2,0) covered? It's integer distance from (0,0) and integer distance from (-1,0) too... so it's not coloured.
Ok, the 0,0 and -1, -1:
The point (-4,3) is still uncovered! Proof:
0 - -4 = 4
3 - 0 = 3
Squared, summed, and sqrooted: 5
So marker (0,0) doesn't cover it.
What about marker (-1,-1)
-1 - -4 = 3
3 - -1 = 4
Again, leaving distance 5. So our grid isn;t coloured.
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Non-integer colouring
« Reply #4 on: May 25th, 2006, 6:14am » |
Quote Modify
|
Your analysis is correct, Sjoerd. My argument is flawed... 
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Non-integer colouring
« Reply #5 on: May 25th, 2006, 7:00am » |
Quote Modify
|
[edit]I missed part of SJP's analysis -- he disproved (0,0) and (-1,-1) but not (0,0) and (-1,0) right? If (0,0) and (-1,0) leave any points uncolored axcept the x-axis, disregard all the below...  [/edit]
OK, then I think we can answer question 1 in the plane: two markers cannot be sufficient. WOLG consider markers at (0,0) and (x,y): at least points (x,0) and (0,y) (the axis crossings) will remain uncolored. Certainly, though, by Barukh's analysis, markers at (0,0), (1,0), and (0,1) are sufficient to color the plane: the first two markers color all points except the x-axis and the third marker colors the entire x-axis.
That still leaves Q2 open, as the distance from (1,0) to (0,1) is non-integral, although we know from the axis-crossing argument that at least three markers are required. It also still leaves both questions open in higher dimensions -- the axis-crossing argument doesn't hold in higher dimensions.
--SMQ
|
| « Last Edit: May 25th, 2006, 7:05am by SMQ » |
IP Logged |
--SMQ
|
|
|
Sjoerd Job Postmus
Full Member
Posts: 228
|
|
Re: Non-integer colouring
« Reply #6 on: May 25th, 2006, 9:47am » |
Quote Modify
|
Let's denote our three markers M1, M2 and M3 - since, by our axes-crossing-theorem/argument, we need at least 3 markers...
They must all be integral distance from eachother...
Without loss of generality, we can position our marker first on M1 = (0,0).
The second markers will be on:
M2 = (p,q)
M3 = (r,s)
Yielding:
p^2 + q^2 = n^2
r^2 + s^2 = m^2
and
(p-r)^2 + (q-s)^2 = o^2
p^2 - 2pr + r^2 + q^2 - 2qs + s^2 = o^2
Substracting m^2 and n^2
-2pr - 2qs = o^2 - n^2 - m^2
2 * (-pr - qs) = o^2 - n^2 - m^2
0 or 2 of these are even... We know all numbers are integer, so -pr and -qs will be an even, or an odd number. Twice that, will be even.
o^2 - n^2 - m^2 = even
If three of these were odd:
odd + odd + odd ?= even... NO!
Or one of these:
even + even + odd ?= even... NO!
So two or none must be odd.
But, where to place these? I assume a pythagorean triplet would work... but would it...
Let's take
M1 = (0,0)
M2 = (4,0)
M3 = (4,3)
Just for kicks...
It won't work... (0,3) isn't covered. Would covering that one, be sufficient? I don't know.
Who knows, help us all, and give us the answer!
---
Edit: Anyhow, I think for Q2, the answer is 4... why, I dunno, because 3 wouldn't be enough
|
| « Last Edit: May 25th, 2006, 10:01am by Sjoerd Job Postmus » |
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Non-integer colouring
« Reply #7 on: May 27th, 2006, 9:24am » |
Quote Modify
|
Question 2 doesn't state expicitly that markers can be placed only at grid points. But I assume this is the case?
|
|
IP Logged |
|
|
|
Sjoerd Job Postmus
Full Member
Posts: 228
|
|
Re: Non-integer colouring
« Reply #8 on: May 27th, 2006, 11:18am » |
Quote Modify
|
on May 27th, 2006, 9:24am, Barukh wrote:| Question 2 doesn't state expicitly that markers can be placed only at grid points. But I assume this is the case? |
|
I assume this is the case. What would be your solution if this isn't true?
Ok... yet another thing...
Let us consider the grid, and the integer-distance-marker-problem.
Let's think of three markers, M1, M2 and M3
Let's consider the mid-point of any of the sides, call it S - without a reason
find angle M1,S,M3, and distance S,M3...
Now, on the line through S and M3, mark another marker, the same distance away from S, but on the other side, obviously it is on a grid point. But, now our question is: Is the distance from M3 to M3' integer?
I can't proof it yet... but I don't have enough time!
Let us consider, WOLG, M1 = (0,0), if your solution doesn't have a marker there, move it to there!
M2 = (a,b)
M3 = (c,d)
Midpoint S will be: (.5a, .5b)
Let's flip M3 in M2...
((-(c - .5a) + .5a), (-(d - .5b) + .5b))
Which makes:
M3' = ((-c + a), (-d + b))
Distance?
M3 - M3'
sqrt((c - (-c + a))^2 + (d - (-d + b))^2)
Let's see...
sqrt{(2c - a)^2 + (2d - b)^2}
Now, is this value an element from N? I don't know...
But we already know that
sqrt{(c-a)^2 + (d-b)^2} is from N
sqrt{a^2 + b^2} is from N
sqrt{c^2 + d^2} is from N
Now, ((-c + a), (-d + b)) must be of integer distance from M1 and M2..., because, in reality, all we did was take the triangle, and rotate it 180 degrees in midpoint S ...
So...
sqrt{(-c+a)^2 + (-d + b)^2} is from N
sqrt{((-c+a)-a)^2 + ((-d+b)-b)^2} would mean
sqrt{(-c)^2 + (-d)^2} is from N, wich is a duh-statement.
I'll continue it when I have pencil and paper near me... (read: Not Now!)
|
|
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: Non-integer colouring
« Reply #9 on: May 27th, 2006, 12:02pm » |
Quote Modify
|
on May 27th, 2006, 9:24am, Barukh wrote:| Question 2 doesn't state expicitly that markers can be placed only at grid points. But I assume this is the case? |
|
Sure it is! (Edited the problem statement to make this explicit.)
|
|
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Non-integer colouring
« Reply #10 on: May 28th, 2006, 6:32am » |
Quote Modify
|
on May 25th, 2006, 9:47am, Sjoerd Job Postmus wrote:
Let's take
M1 = (0,0)
M2 = (4,0)
M3 = (4,3)
Just for kicks...
It won't work... (0,3) isn't covered. Would covering that one, be sufficient? I don't know.
Who knows, help us all, and give us the answer! |
|
Sjoerd, I think your 4-point configuration is sufficient. Here’s what I came with.
First, I took 2 points (0,0) and (4,0) and tried to identify all other points that are at integer distances from this pair. This means to solve a pair of quadratic Diophantine equations (QDE):
x2 + y2 = m2,
(x-4)2 + y2 = n2
It is immediately clear that m-n should be even. Several cases need to be considered (I won’t make the same mistake again!):
1. m = n. This yields the unique solution on an x-axis: (2,0).
2. |m – n| = 4. This yields an infinite number of solutions (m, 0) on x-axis.
3. |m – n| = 2. This is the most interesting case. Combining all three equations together, I got m = |2x-3|, and plugging this into the first equation, finally:
-3x2 + y2 + 12x – 9 = 0.
Now, there is a standard way to solve such QDE (there is even a nice online solver). In this particular case, there are two basic solutions (1, 0), (4, 3) that generate two infinite families of solutions according to the following recurrent formula:
xk+1 = 2xk - yk – 2,
yk+1 = -3xk + 2yk + 6.
I immediately noticed that the first family – except two solutions - consists of solutions in the 2nd quadrant only, while the second family similarly consists almost of solution in the the 4th quadrant.
Next, I took another pair of points - (0,0), (0,3) – and made the same derivation. The QDE to solve this time was
x2 - 8y2 + 24y – 16 = 0,
which again has two basic solutions (0, 1), (0, 2) and two iterative families:
xk+1 = 3xk + 8yk – 12,
yk+1 = xk + 3yk - 3.
Now, these families generate solutions in the 1st and 3rd quadrants, except a few cases on the axes.
Conclusion: the only point not on the axes at the integer distance from the triple (0,0), (4,0), (0,3) is the point (4,3). This point is at the irrational distance from the points (-4,0) and (0,-3). Therefore, the four points mentioned by Sjoerd colour the whole plane.
If I didn’t make any mistake, I’m sure an easier demonstration must exist.
|
|
IP Logged |
|
|
|
Sjoerd Job Postmus
Full Member
Posts: 228
|
|
Re: Non-integer colouring
« Reply #11 on: May 28th, 2006, 7:14am » |
Quote Modify
|
Woah! This is way above my head... hope I'll be able to do such math one-day too...
So, we know there's one solution.
I also suggest that: Any Primitive Pythagoras Triplet, plus the point obtained by rotating the right angle around the midpoint of the hypothenusa(sp?) will yield another valid solution.
So: Let's have Primitive Pyth.Triplet: (a,b,c), then
(0,0)
(a,0)
(a,b)
(0,b)
Yields a valid solution.
Iff this is true, then
(0+n,0+m)
(a+n,0+m)
(a+n,b+m)
(0+n,b+m)
is also a valid solution.
n and m being whole integer values, that are not related to those mentioned in Barukh's proof.
Do I need to get you more stuff to proof?  j/k... I'm just the trial-and-error bloke, and the rest of you are more into the rigorous proof thing...
Me too, actually, but my math isn't good enough to do it for this hard stuff.
Thanks! Now I need to either find a failure in your proof using: There exists a value for which it doesn't work, thingy... or wait for someone else to go through your proof step-by-step, and find that it's correct. I think it is, though... makes sense.
|
|
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: Non-integer colouring
« Reply #12 on: May 28th, 2006, 7:31am » |
Quote Modify
|
on May 28th, 2006, 6:32am, Barukh wrote:
Sjoerd, I think your 4-point configuration is sufficient. |
|
Well done guys.
Is a 4-point configuration also necessary?
|
| « Last Edit: May 28th, 2006, 7:35am by JocK » |
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Non-integer colouring
« Reply #13 on: May 28th, 2006, 10:46am » |
Quote Modify
|
on May 28th, 2006, 7:14am, Sjoerd Job Postmus wrote:| Thanks! Now I need to either find a failure in your proof using: There exists a value for which it doesn't work, thingy... or wait for someone else to go through your proof step-by-step, and find that it's correct. I think it is, though... makes sense. |
|
Unfortunately, my above argument is broken: I just realized that in the first case when (xn, yn) is a solution, so is (xn, -yn), and likewise in the second case. So, both cases generate solutions in every quadrant.
Fortunately, the result is still valid: the argument may be repaired by considering the ratios of xn/yn in both cases.
This is intimately related to continued fractions. I remember Icarus once or twice posted a method of solving such recurrences.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Non-integer colouring
« Reply #14 on: May 28th, 2006, 11:41am » |
Quote Modify
|
The method I have posted solves homogenous linear recurrences with constant coefficients. Unfortunately, your recurrence is not homogenous.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sjoerd Job Postmus
Full Member
Posts: 228
|
|
Re: Non-integer colouring
« Reply #15 on: May 28th, 2006, 1:13pm » |
Quote Modify
|
Well... let me ask something. because we just have a rectangle, if there is any problem(non-coloured item), we have 4, 8, 12, etc problems.
Let's say (x,y) isn't coloured. Then, I say... (4-x,y) isn't coloured, (x,3-y) isn't coloured, and (4-x,3-x) isn't coloured. See why?
So, we can actually ignore the solutions in other quadrants then the first, because those are just copies.
Maybe this helps a bit more?
|
|
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Non-integer colouring
« Reply #16 on: May 29th, 2006, 8:15pm » |
Quote Modify
|
on May 28th, 2006, 6:32am, Barukh wrote:If I didn’t make any mistake, I’m sure an easier demonstration must exist.
|
|
You don't need to solve the QDEs separately -- two hyperbolas intersect in 4 points.
By the triangle inequality, and parity, (x,y) satisfies one of the following 5*4 pairs of equations:
r1 = |(x, y)| - |(x-4, y)| = 0, +/-2, +/-4,
r2 = |(x, y)| - |(x, y-3)| = +/-1, +/-3.
r1=0 or +/-4 means y=0. Since (3,4,5) is the only Pythagorean triple with a 3, x=+/-4, but (-4,0) is no good, and (4,0) is taken.
Similarly, r2=+/-3 means x=0; (3,4,5) is also the only triple with a 4, so again y=+/-3 is no good.
(r1,r2)=(2,1) implies (x,y)=(4,3), which we have.
(r1,r2)=(+/-2, -/+1) implies (via Mathematica, i.e., a finite calculation but I'm lazy) that (x,y) = (4(10+/-3[sqrt]6), 27-/+8[sqrt]6)/23, no good.
Finally, (r1,r2)=(-2,-1) implies (x,y) = (20, 21)/23, no good.
In fact this argument shows that if infinitely many points in the plane have mutual distances all integral, then they are all collinear (specifically, given any non-degenerate triangle, there are only finitely many places for the other points). Hence we can start with any Pythagorean triple and mark uncolored points all willy-nilly, and it'll only take a finite number of markers. But:
Question 3: For any N, find N non-collinear markers, on gridpoints, with mutual distances all integral, which do not color the whole grid.
|
|
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: Non-integer colouring
« Reply #17 on: May 30th, 2006, 12:12pm » |
Quote Modify
|
Guys, I'm gonne give you a BIG helping hand here:
3 markers at integer distance suffice to colour all gridpoints ... 
Try it! 
|
| « Last Edit: May 30th, 2006, 12:16pm by JocK » |
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Non-integer colouring
« Reply #18 on: May 30th, 2006, 8:25pm » |
Quote Modify
|
on May 30th, 2006, 12:12pm, JocK wrote:| 3 markers at integer distance suffice to colour all gridpoints ... |
|
And all this time I've been trying to prove they don't...
Any lattice triangle has rational area K (in fact 2K is an integer by Pick's theorem). Hence if the sides a,b,c are integers, it's Heronian. (in fact, by Hero's formula, (a+b+c)4 = 4(2K)2 = 0 mod 2, so a+b+c is even, and then 2K is even, hence K is an integer). (It's worth noting that given an integral lattice triangle, there will be lots of rational points a rational distance from all three vertices (e.g., the base of each altitude).)
For a Heronian triangle with sides lengths (a,b,c) to color all lattice points, it must not be a right triangle, and no side may be parallel to an axis. In particular, each of a,b,c must be the hypotenuse of some Pythagorean triple, but (a,b,c) itself can't be Pythagorean.
Take a Heronian triple (a,b,c). For each way of writing a2=u2+v2, with u,v>0, there are two rational points (p,q) a distance b from (0,0), and c from (u,v). If (p,q) is integral, and p != 0,u and q != 0,v, then for each |i|<a, |j|<b, with i=a, j=b mod 2, check for integral points (x,y) satisfying
|(x,y)| - |(x-u,y-v)| = i,
|(x,y)| - |(x-p,y-q)| = j.
If there are no such (x,y) other than the 3 vertices, congratulations.
Using this list of primitive Heronian triangles with sides < 300, I checked all 2080 Heronian triangles with sides < 300. Assuming my program is correct, none of them work.
|
| « Last Edit: May 31st, 2006, 1:32am by Eigenray » |
IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Non-integer colouring
« Reply #19 on: Jul 30th, 2007, 3:12am » |
Quote Modify
|
on May 30th, 2006, 12:12pm, JocK wrote:| 3 markers at integer distance suffice to colour all gridpoints ... |
|
Anyone have any thoughts on this?
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Non-integer colouring
« Reply #20 on: Jul 30th, 2007, 1:52pm » |
Quote Modify
|
on Jul 30th, 2007, 3:12am, Eigenray wrote:
Anyone have any thoughts on this? |
|
From your above, in the case where a (or b) is even, and so i (or j) can be 0, is |(x,y)| - |(x-u,y-v)| = 0 (or |(x,y)| - |(x-p,y-q)| = 0) sufficient to establish that |(x,y)| is an integer? If not, is it within the realm of possibility that one or more solutions could have been missed by your program because it found an erroneous disqualifying point (x,y) where |(x,y)| - |(x-u,y-v)| = 0 but |(x,y)| is not an integer? Assuming your program is otherwise correct and the bounds sufficient, that's the only potential loophole I can find...
--SMQ
|
|
IP Logged |
--SMQ
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: Non-integer colouring
« Reply #21 on: Jul 30th, 2007, 11:58pm » |
Quote Modify
|
That's a good point, but it turns out (empirically, no proof) that |(x,y)| is always an integer. The only possible exception would be if both i=j=0, so (x,y) is the intersection of the bisectors from (0,0) to (u,v) and (p,q), which works out to
{ x, y }= { [v(p2+q2)-q(u2+v2)]/[2(pv-qu)], [u(p2+q2)-p(u2+v2)]/[2(qu-pv)] }
But you agree with the rest of the reasoning? I use Mathematica's Rest@OrderedSumOfSquaresRepresentations[2,a2] to find the possibilities for (u,v) [WLOG, u > v > 0; Rest drops the first term which is (a,0)]. For each (u,v), I find
(p,q) = t/a (u,v)  h/a (-v,u), where t=(a2+b2-c2)/(2a), h =  {b2-t2}.
h is the altitude from side a, so is rational because of Heronity. If (p,q) is integral, and not on the same row or column as (0,0) or (u,v), I look for a 4-th point (x,y). The expression for x,y in terms of u,v,p,q,i,j is nasty, but in all cases I've found such a point, and checked to make sure there were no false positives.
The tricky part seems to be generating the Heronian triplets to test: this parameterization doesn't produce primitive triplets, only one from each similarity class, and the gcd can be arbitrarily large. I don't actually know a good way to produce all triplets with max side < M. And it's not enough to just consider primitive triplets, since the property we're looking for depends on the embedding. For example, the smallest multiple of (5,5,6) which can be embedded in a lattice with no side parallel to an axis is 13*(5,5,6).
|
| « Last Edit: Jul 31st, 2007, 12:46am by Eigenray » |
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Non-integer colouring
« Reply #22 on: Jul 31st, 2007, 6:02am » |
Quote Modify
|
on Jul 30th, 2007, 11:58pm, Eigenray wrote:| But you agree with the rest of the reasoning? |
|
I think I need an explanation how does the 4th point prove anything.
|
|
IP Logged |
|
|
|
SMQ
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 2084
|
|
Re: Non-integer colouring
« Reply #23 on: Jul 31st, 2007, 7:38am » |
Quote Modify
|
on Jul 30th, 2007, 11:58pm, Eigenray wrote:| But you agree with the rest of the reasoning? |
|
I do. To restate, just to be sure I'm understanding: consider any three lattice points at mutually-integer distances, and the triangle they form:
1) The area of any triangle with verteces on the lattice points is clearly integer or half-integer (construct the rectangular bounding-box with sides parallel to the lattice axes, subtract the areas of the at-most-three right triangles outside the original triangle).
2) Any triangle with integer side lengths and integer or half-integer area is, by definition, Heronian.
3) For any right triangle, a fourth point at the remaining corner of a rectangle created by rotating a copy of the triangle 180 degrees and joining the hypotenuses is clearly at an integer distance from all three original points (and therefore not colored by any of the three original points).
4) For any triangle with a side parallel to one of the lattice axes, the lattice point at the base of the altitude to that side will clearly be at an integer distance from all three original points (unless the parallel side is a leg of a right triangle, in which case observation (3) applies instead).
5) WLOG, Let the verteces of the triangle be at coordinates (0,0), (u,v) and (p,q) where p, q, u and v are all integers, u and v are positive, and |(u,v)|, |(p,q)|, and |(u-p),(v-q)| are integers. By parity and the triangle inequality, any point (x,y) at an integer distance from all three points of the triangle will be at an intersection of the hyperbolas given by |(x,y)| - |(x-u,y-v)| = +/- i and |(x,y)| - |(x-p,y-q)| = +/- j for some 0 < i <|(u,v)|, i = |(u,v)| mod 2, 0 < j <|(p,q)|, j = |(p,q)| mod 2.
6) If any such (x,y) coincides with a lattice point and is not a vertex of the original triangle then none of the three original points colors (x,y) and so together they do not constitute a solution.
Quote:| The tricky part seems to be generating the Heronian triplets to test |
|
Although the fact that the triangles are Heronian is interesting, I'm not sure it's helpful. What if instead of generating Heronian triples, you generate Pythagorean triples? Generating all Pythagorean triples up to some max side < M is fairly straightforward. Then, given Pythagorean triples (u,v,a) and (s,t,b) check the up-to-eight possible points (p,q) = { (s,t), (s,-t), (-s,t), (-s,-t), (t,s), (t,-s), (-t,s), (-t,-s) }, p <> u, q <> v for integer distance to (u,v), then search for (x,y) as before for any that form non-degenerate, non-right triangles with (0,0).
--SMQ
|
| « Last Edit: Jul 31st, 2007, 3:50pm by SMQ » |
IP Logged |
--SMQ
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Non-integer colouring
« Reply #24 on: Jul 31st, 2007, 10:31am » |
Quote Modify
|
Aha! I think I've got it! The intersection of two hyperbolas! Thanks, SMQ. BTW:
on Jul 31st, 2007, 7:38am, SMQ wrote:| By parity and the triangle inequality, any point (x,y) at an integer distance from all three points of the triangle will be at an intersection of the hyperbolas given by (x2 + y2) - [(x-u)2 + (y-v)2] = i2 and (x2 + y2) - [(x-p)2 + (y-q)2] = j2 for some 0 < i <|(u,v)|, i = |(u,v)| mod 2, 0 < j <|(p,q)|, j = |(p,q)| mod 2. |
|
these are not exactly hyperbolas.
Eigenray, how do compute this intersection? Again using Mathematica?
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print