 Author
Author |
Topic: Periodic Poles (Read 1639 times) |
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Periodic Poles
« on: Jan 5th, 2006, 7:32pm » |
 Quote Quote  Modify Modify
|
Evaluate
 n=- n=- 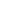 (x - n)-k (x - n)-k
where k > 1 is an integer.
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Periodic Poles
« Reply #1 on: Jan 11th, 2006, 2:19pm » |
 Quote Quote  Modify Modify
|
Hint: Take the case k=2 first and look for a function whose numerator involves pi. For the latter cases of k, just differentiate this function the appropriate number of times.
|
| « Last Edit: Jan 11th, 2006, 2:21pm by Michael Dagg » |
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
SWF
Uberpuzzler
    

Posts: 879
|
 |
Re: Periodic Poles
« Reply #2 on: Jan 11th, 2006, 5:26pm » |
 Quote Quote  Modify Modify
|
I don't see if this fits with Michael's hint, but one thing that can be done is to convert to a different series involving Riemann zeta functions of even integers:
Consider only 0<x<1, because the integer part of x does not affect the sum. The sum has a 1/x term when n=0. Expand the rest of the sum in a Taylor series about x=0 (taking multiple derivatives with resepect to x is easy). That gives something like ( z(y) is Riemann zeta function ):
For k=even (sum is over m=0,2,4,6,...): 1/x + [sum] 2(k+m-1)!*z(k+m)*x^m / (k-1)! / m!
For k=odd (sum is over m=1,3,5,...): 1/x - [sum] 2(k+m)!*z(k+m)*x^m / (k-1)! / m!
Every zeta function above has an even argument and is therefore expressible in terms of pi. Perhaps there is some zeta function identity that is related to Michael's hint which will simplify the expressions.
|
|
 IP Logged IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Periodic Poles
« Reply #3 on: Jan 11th, 2006, 6:29pm » |
 Quote Quote  Modify Modify
|
The connection between this series and the Riemann zeta function is part of why I felt this was intriguing enough to post. I had ideas of exploring this once the original problem is solved. However, the Riemann connection is not necessary to find a solution. The series can be expressed using elementary functions.
A further hint:
| hidden: | | If you can find another function with the same poles and zeros, having the same behavior at those poles and zeros, then the ratio of the two is analytic everywhere - and if the two also behave the same at infinity... |
|
|
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Periodic Poles
« Reply #4 on: Jan 13th, 2006, 5:12pm » |
 Quote Quote  Modify Modify
|
Poisson summation is also useful.
|
|
 IP Logged IP Logged |
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
    

Gender: 
Posts: 1948
|
 |
Re: Periodic Poles
« Reply #5 on: Feb 10th, 2006, 9:03pm » |
 Quote Quote  Modify Modify
|
The Poisson summation formula states that, under certain conditions on f, we have
[sum]n=-oooo f(n) = [sum]n=-oooo F(n),
where, for lack of better typography, F denotes the Fourier transform
F(n) = [int]-oooo f(x)e-2pi inxdx.
In particular, this holds when f is holomorphic and (1+x2)|f(x+iy)| is bounded in some horizontal strip containing the x-axis, so we may apply it to the function
f(z) = (z + t)-k, k>2,
supposing first that Im(t) > 0. In this case
F(n) = [int] g(x) dx, where g(z) = e-2pi inz/(z+t)k.
Now, g is meromorphic with a single pole at z=-t, of residue
(-2pi i n)k-1/(k-1)! e2pi int.
If |z|=R is sufficiently large, then |f(z)| < (R/2)-k. Also, if n<0, then |e-2pi inz| = e2pi n Im(z) <1 for z in the upper halfplane, so |g(z)| < (R/2)-k over a large semi-circle, and the integral goes to 0 since k>1. Since g has no pole in the upper halfplane, we have F(n) = 0 for n<0. Similarly, if n>0, then the integral of g over a large semicircle in the lower halfplane goes to 0. Going around clockwise, we pick up -(2 pi i) times the residue, so
F(n) = (-2pi i)k/(k-1)! nk-1e2pi i nt.
Thus, for Im t > 0, we have by Poisson summation
[sum] (n+t)-k = (-2pi i)k/(k-1)! [sum]n=1oo nk-1e2pi i nt.
If k=2, we can write this as
[sum] (n+t)-2 = -4 pi2 [sum] n e2pi i nt
= -4 pi2 e2pi it/(1-e2pi it)2
= -4pi2/(e-pi it-epi it)2
= -4pi2/(-2i sin pi t)2
= pi2/sin2(pi t).
Moreover, since both sides are meromorphic on C (the sum converging uniformly on compact subsets of C\Z), this holds for all t not an integer. Finally, if we differentiate both sides (k-2) times, we can also write
[sum] (n - t)-k = 1/(k-1)! dk-2/dtk-2 (pi2/sin2(pi t)).
|
|
 IP Logged IP Logged |
|
|
|
Michael Dagg
Senior Riddler
   

Gender: 
Posts: 500
|
 |
Re: Periodic Poles
« Reply #6 on: Feb 10th, 2006, 11:10pm » |
 Quote Quote  Modify Modify
|
Very nice. Your last line is my hint!
|
|
 IP Logged IP Logged |
Regards,
Michael Dagg
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
    

Boldly going where even angels fear to tread.
Gender: 
Posts: 4863
|
 |
Re: Periodic Poles
« Reply #7 on: Feb 11th, 2006, 8:11am » |
 Quote Quote  Modify Modify
|
The argument that I found which sparked this is (again for the k=2 case):
let f(z) =  (z - n)-2. f is easily seen to be convergent for all non-integral z, and is obviously periodic of period 1, with double poles at each integer. (z - n)-2. f is easily seen to be convergent for all non-integral z, and is obviously periodic of period 1, with double poles at each integer.
g(z) =  2sin-2 2sin-2  z is also periodic of period 1 with double poles. Further, both f(z) and g(z) have identical singular part at each pole. I.e. f(z) - g(z) is analytic everywhere. z is also periodic of period 1 with double poles. Further, both f(z) and g(z) have identical singular part at each pole. I.e. f(z) - g(z) is analytic everywhere.
Let z = x+iy, for real x, y. The limit of f(x+iy) as |y| --> oo is easily seen to be 0. |sin(x+iy)|2 = cosh2y - cos2x , so g(x+iy) --> 0 as |y| --> oo as well.
Thus f(z)-g(z) must be bounded on the strip [0,1] + iR. By periodicity, it is also bounded everywhere. The only bounded analytic functions on the entire plane are constants, so f(z)-g(z) = k, and since the limit as y --> oo is 0, k=0.
Hence  (z - n)-2 = (z - n)-2 =  2sin-2 2sin-2  z. z.
______________________________________________________________________
For k > 2, you can indeed use the differentiation method on the k=2 case. But this can get messy as k gets larger. It seems to me that the proof of the k=2 case above offers an alternative approach.
For each k, find a period 1 function g(z) whose only poles are at the integers and whose singular part at z=0 is 1/zk, and for which g(x+iy) --> 0 as |y| --> oo. All such functions are necessarily equal, by the argument used above.
So by playing around with sin z and cot z, you ought to be able to construct formulas for each value of k simply by matching poles.
|
| « Last Edit: Feb 11th, 2006, 8:17am by Icarus » |
 IP Logged IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
|
 WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register WRITE MATH!
WRITE MATH!
 Home
Home  Help
Help  Search
Search  Members
Members  Login
Login  Register
Register