Author |
Topic: random motion in a rectangle (Read 1977 times) |
|
JocK
Uberpuzzler
Gender: 
Posts: 877
|
 |
random motion in a rectangle
« on: Jan 9th, 2005, 11:06am » |
 Quote  Modify
|
A particle at the centre of a rectangle starts a perfectly random Brownian motion. Given that the likelihood it first hits a longer boundary is twice as large than the likelihood that it hits a shorter boundary first, determine the aspect ratio (ratio of long side to short side) of the rectangle.
|
|
 IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
|
Re: random motion in a rectangle
« Reply #1 on: Jan 9th, 2005, 12:01pm » |
Quote Modify
|
::roughly 1.4::?
As a (vaguely) educated guess
|
|
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: random motion in a rectangle
« Reply #2 on: Jan 9th, 2005, 1:55pm » |
Quote Modify
|
on Jan 9th, 2005, 12:01pm, rmsgrey wrote:::roughly 1.4::?
As a (vaguely) educated guess |
|
Close, but no sigar. (Rounded off to one decimal place, the solution is not 1.4.)
|
|
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: random motion in a rectangle
« Reply #3 on: Jan 9th, 2005, 3:06pm » |
Quote Modify
|
Another guess, ::1.62::
Or maybe ::1.57::
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: random motion in a rectangle
« Reply #4 on: Jan 9th, 2005, 5:12pm » |
Quote Modify
|
Was this puzzle inspired by SIAM 2002 Problem #10?
It has a rectangle of 10 x 1 and a probability of hitting one of the shorter sides of only 1 in 2605802 (!)
So I think the ratio L/W should be pretty small.
How about 1.15?
|
| « Last Edit: Jan 10th, 2005, 10:39am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
BNC
Uberpuzzler
Gender:
Posts: 1732
|
|
Re: random motion in a rectangle
« Reply #5 on: Jan 9th, 2005, 10:14pm » |
Quote Modify
|
My guess would be ::1.73::
|
|
IP Logged |
How about supercalifragilisticexpialidociouspuzzler [Towr, 2007]
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: random motion in a rectangle
« Reply #6 on: Jan 10th, 2005, 12:41am » |
Quote Modify
|
on Jan 9th, 2005, 10:14pm, BNC wrote:| My guess would be ::<hidden>:: |
|
That's what I thought of as well just before I went to sleep yesterday..
It's what you get by considering a wave starting at the center and looking what part of the energy hits what side. But the result for the similar problem mentioned by Thud doesn't correspond to the one given in the page he links to.
|
| « Last Edit: Jan 10th, 2005, 1:16am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
BNC
Uberpuzzler
Gender:
Posts: 1732
|
|
Re: random motion in a rectangle
« Reply #7 on: Jan 10th, 2005, 1:37am » |
Quote Modify
|
on Jan 10th, 2005, 12:41am, towr wrote:
That's what I thought of as well just before I went to sleep yesterday..
It's what you get by considering a wave starting at the center and looking what part of the energy hits what side. But the result for the similar problem mentioned by Thud doesn't correspond to the one given in the page he links to. |
|
Yeah, I noticed it too... 
|
|
IP Logged |
How about supercalifragilisticexpialidociouspuzzler [Towr, 2007]
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: random motion in a rectangle
« Reply #8 on: Jan 10th, 2005, 2:18am » |
Quote Modify
|
The reason why it's wrong is also mentioned in the page Thud links to, the capture at the edges changes the distribution inside the rectangle (so it stops being a nice gaussian wave).
I think I'll wait to see what my simulation will yield as a result before making any more guesses. But that might take the rest of the day to finish.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: random motion in a rectangle
« Reply #9 on: Jan 10th, 2005, 9:50am » |
Quote Modify
|
Here's my try: [smiley=square.gif]1.29...[smiley=square.gif]
|
| « Last Edit: Jan 10th, 2005, 11:22am by Barukh » |
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: random motion in a rectangle
« Reply #10 on: Jan 10th, 2005, 1:38pm » |
Quote Modify
|
I suspect my simulation program must be screwed up, I get about 1.70, which all things considering may be a bit high.
Not much reason to hide it, we're just bidding numbers here without further justifaction.
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: random motion in a rectangle
« Reply #11 on: Jan 11th, 2005, 9:23am » |
Quote Modify
|
Barukh... I think you are close... very close..! 
(Getting a rough approximation shouldn't be too difficult... I'm very curious though what accuracy will be reached...)
|
|
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: random motion in a rectangle
« Reply #12 on: Jan 11th, 2005, 5:23pm » |
Quote Modify
|
I am convinced that probability should be governed by the same PDE as diffusion. If for a point (x,y) the probability of random walk reaching the long vertical sides before one of the horizontal sides is [phi](x,y), and the rectangle has dimensions 2 by 2*h, [phi] must satisfy:
0 = [partial]2[phi]/[partial]x2 + [partial]2[phi]/[partial]y2 with boundary conditions [phi]([pm]1,y) = 1 and [phi](x,[pm]h)=0
Solution for probability at any point in the rectangle is:
[phi](x,y) = (4/[pi])*[sum] (-1)n/(2n+1) cos(any) cosh(anx)/cosh(an)
where sum is over n=0 to infinity and an=(2n+1)[pi]/2/h. For probability of reaching one of the long sides first to be double of it reaching a short side first, [phi](0,0)=2/3:
[pi]/6 = [sum] (-1)n/(2n+1)/cosh((2n+1)[pi]/2/h)
Solving for h gives: 1.279261571171...
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: random motion in a rectangle
« Reply #13 on: Jan 12th, 2005, 4:17am » |
Quote Modify
|
SWF, I am just curious how did you solve the last equation for h?
From different sources, I've got an elementary expression that can be easily computed and gives the same result as SWF's, but its derivation includes a few steps that I still don't understand. I will try to consolidate my efforts and explain it here later.
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: random motion in a rectangle
« Reply #14 on: Jan 12th, 2005, 6:52am » |
Quote Modify
|
Quote:| [pi]/6 = [sum] (-1)n/(2n+1)/cosh((2n+1)[pi]/2/h) |
|
According to the above notation, what is w/x/y/z?
What does the above formula give for h = 10?
|
| « Last Edit: Jan 12th, 2005, 6:56am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: random motion in a rectangle
« Reply #15 on: Jan 12th, 2005, 7:04pm » |
Quote Modify
|
Barukh, I just solved that last equation numerically. I would be interested in the more elementary solution. Often using functions of a complex variable and conformal mapping a more simple solution can be found that does not require an infinte series. By the way I found another expression that can be used to find h:
[pi]/12 = [sum] (-1)n tan-1( exp(-(2n+1)[pi]/2/h) )
ThudandBlunder, I have no idea what you mean by "w/x/y/z", unless some of the special symbols like pi or subscripts are showing up strangely for you. When h is 10, that formula gives probability of reaching a long side first as 0.999999616...
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
Here’s what I know so far.
First of all, it is clear that the SIAM Challenge #10 mentioned by T&B, is just the inverse of the problem stated (up to parameters given). Also, it was clear to me that if I don’t want to rely on the Monte-Carlo method, I need some advanced technique from high math that I don’t master. So, I went to learn what the winners of the contest had to suggest. In what follows, I will describe what I liked most. Sometimes, I will omit details – partially because I cannot explain them, and partially because they are too technical.
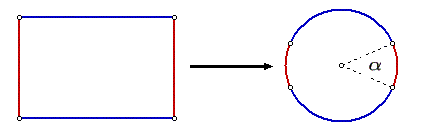
I thought that if we were given the circle with the marked arcs - instead of the rectangle with long and short sides – then the solution would be trivial (see the drawing), since the probability would be simply [alpha]/[pi]. The real question is: how do we transform the rectangle to the circle so that the probability of hitting the small arc is the same as the probability of hitting the small side? It turns out that the needed transformation is the conformal mapping – as was correctly suggested by SWF. The conformal mapping (CM) is a transformation that preserves angles.
Hmm, if you ask me why CM leaves the sought probability unchanged – I will say that I don’t understand. One of the possible answers would be that the Brownian process stated in the problem obeys the Laplace Equation, and the solutions of the latter are preserved under CM (my friend mathematician I talked to this morning, confirmed this and told it’s not difficult to prove).
Now, let’s see, how do we get the required transformation. This is dealt in Complex Analysis and took me a lot of time to understand at the very high level. Usually, it is done in two steps: first, the rectangle is transformed onto the half-plane using Complete Elliptic Integrals of the first kind, and then the half-plane is transformed onto the unit circle using Mobius transformations. It sounds frightening, but the essentials are easy to comprehend: the complete elliptic integral is a function E(k) of the parameter k, and it turns out that the aspect ratio r of the rectangle and the arc length [alpha] of its circle image are related by the following formula:
r = E(cos([alpha]/2))/E(sin([alpha])/2)
(again, I don’t know how to prove this, but it shouldn’t be difficult for the specialist).
At this point, it seems that we didn’t get too far. Fortunately, there is an elegant way to evaluate elliptic integrals using the Arithmetic-Geometric Mean (AGM) of 2 numbers. In fact, we have:
E(k) = AGM(1, k).
The following nice article (section 4.2) provides an insight. AGM is such a simple algorithm that can be programmed at the advanced calculator.
Going back to the conditions of the problem, we see that [alpha] = [pi]/3, and therefore r = AGM(1, [sqrt]3/2) / AGM(1, 1/2) = 1.27926157117100..
It is interesting to mention that for the problem posted at SIAM Challenge, this approach also works, but requires an iteration process to find the [alpha].
|
| « Last Edit: Jan 13th, 2005, 8:12am by Barukh » |
IP Logged |
|
|
|
JocK
Uberpuzzler
Gender:
Posts: 877
|
|
Re: random motion in a rectangle
« Reply #17 on: Jan 13th, 2005, 12:33pm » |
Quote Modify
|
Nice job SWF and Barukh!
|
|
IP Logged |
solving abstract problems is like sex: it may occasionally have some practical use, but that is not why we do it.
xy - y = x5 - y4 - y3 = 20; x>0, y>0.
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: random motion in a rectangle
« Reply #18 on: Jan 13th, 2005, 8:53pm » |
Quote Modify
|
I found deciding that the probability was a solution to Laplace equation was the tough part. How to solve this partial differential equation in a rectangle with simple boundary conditions is fairly well known- at least the solution by infinite series is. As for this probability following Laplace equation, I justified to myself by noticing that starting at the center of a circle, the first point reached on the cirfumference is equally likely all around. So [phi] (as defined above) in the center of the circle equals the mean value of [phi] on the circumference. I remembered that this is a property of solutions to the Laplace Equation.
Barkuh, after you suggested there is an elementary solution, I briefly tried conformal mapping, but immediately quit upon seeing elliptic integrals. I was not familar with that AGM relation to elliptic integrals. Thanks for explaining all of that.
Here is a side exercise: Starting with the expression I gave above where [pi]/6=...cosh()..., how did I convert it to [pi]/12=...arctan()...? (complex variable transformations not required).
|
|
IP Logged |
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: random motion in a rectangle
« Reply #19 on: Jan 15th, 2005, 1:53am » |
Quote Modify
|
cosh(x) = (ex+e-x)/2
1/cosh(x)
= 2e-x(1/(1+e-2x))
= 2[sum](e-x)2i+1
Let x = [(2n+1) [pi] /2h]
Sub this expression in the formula involving cosh.
This will give us a double sum expression.
Interchange the order of summation, the inner sum then becomes the arctan series and we are done!!
-- AI
|
| « Last Edit: Jan 15th, 2005, 1:58am by TenaliRaman » |
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print