Author |
Topic: A Prisoner & 100 light bulbs (Read 2571 times) |
|
mattian
Senior Riddler
 
Gender: 
Posts: 404
|
Inspired by the now famous 100 prisoners problem, I have derived a new riddle. It actually doesn't relate to the original in any way except for the cast of characters - light bulbs, prisoners and cells.
Here is the riddle: (Please be aware of updates added to the end of this post)
-----------------------------------------------
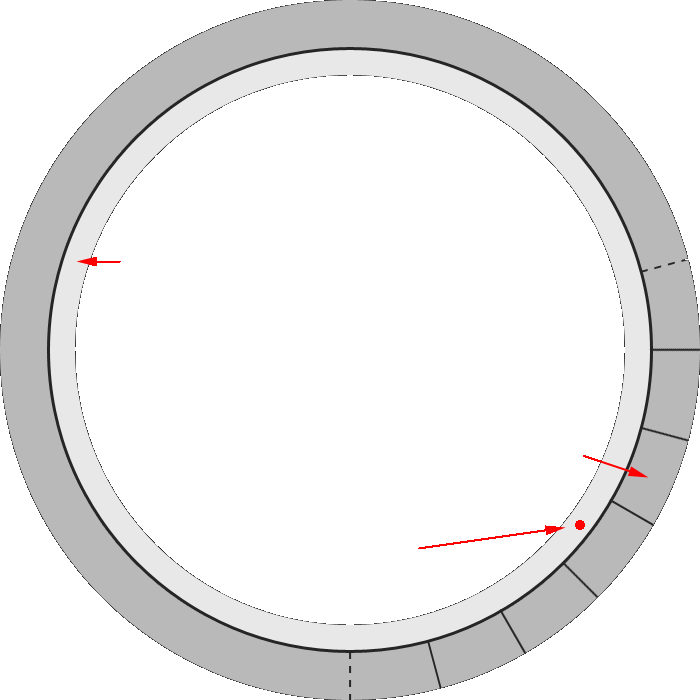
A circular prison has its cells positioned uniformly around its circumference. Each cell has a light bulb. Each room also has a button which clicks each time it is depressed. Each button controls an arbitrary light bulb in one of the cells. For example, if the light bulb connected to a particular button is on and the button is pushed, that light bulb will go off, and vice versa.
A circular corridor lies on a circle just inside the circle of cells and there is a single door from the corridor into each cell.
A prison guard gives the sole prisoner some instructions and teleports him into the circular corridor to an arbitrary position. His instructions are to establish which buttons are connected to which bulbs and to declare it when he knows the complete solution in exchange for his freedom. The prisoner may make his declaration if and only if he knows the configuration of the button-bulb connections. His declaration will be made from within the corridor where he is able to reference doors in his solution.
The following facts apply:
1. The prisoner does not know how many cells there are in the prison.
2. The prisoner may visit the cells in any order.
3. The prisoner does not know the initial state of any of the bulbs.
4. The prisoner does not know any of the relationships between buttons and bulbs.
5. The switch may indeed be connected to the bulb in the same cell.
6. The relationships between buttons and bulbs are entirely random (white noise). There is no definable bias.
Question 1 - What strategy can the prisoner employ to guarantee his freedom?
Question 2 - How can the prisoner minimize the number of cell visits he needs to make before he can declare the solution?
Some wise-guy filters (disclaimers):
1. The buttons always work.
2. The bulbs burn entirely cold and will never burn out.
3. The prisoner cannot gain physical access to the bulbs in order to break them or damage them
4. Nothing that the prisoner does can have any effect on the prison except pressing a button in a cell which has only one outcome; a bulb somewhere in the prison comes on (or off).
5. The prison is pristine and exists in a perfect world where on means on and off means off and there is no inbetween.
6. The prisoner cannot beat up the guards.
7. The cells are entirely indistinguishable from each other in every respect other than the state of the light bulb - ON or OFF. There are no special markings, the prisoner doesn't have any crayons handy, no bloodstains may be left behind in any room.
8. Despite any efforts he might make, the prisoner can not extract any positional state information from the button - it always looks the same.
9. All operations on the button must be performed from within the respective cell with the door closed.
10. No information from the outside world will be available to the prisoner when he is inside a cell - the only information available to him from within the cell, is the state of the light bulb in that cell, and what he decides to do with the button (if anything).
11. To be set free, the prisoner must know the absolute solution and may not guess based on probabilities.
12. If you think you have an answer which solves the problem using some trivial "kill the guards, steal the key" solution which doesn't contradict any of the limitations of this puzzle, then this statement says you're wrong.
13. If your name is Nigel_Parsons, your solution is wrong.
14. Doors close automatically, and faster than the prisoner can move from one cell to another. There are no gaps around the door through which light can pass. From the corridor, the prisoner can see the state of only one bulb at a time - when he is entering or leaving a room. Observing the state of a bulb counts as a visit.
Addendum 1:
1a. I just realised that I should not have used "100" in the topic name as the number of cells (and therefore lightbulbs) is arbitrary in this problem.
Addendum 2:
2a. The prisoner does not have access to any measuring equipment.
2b. It is safe to assume that all cells may be visited in reasonable (finite) time. For the purpose of keeping this within scope, let us assume that the number of cells does not exceed 100 (and the prisoner knows this).
2c. It is also safe to assume the prisoner can travel to any cell in reasonable (finite) time, which implies that the area of the prison is also reasonably small and finite. Let us assume that the prison has a diameter no greater than 100 yds (300 ft).
2d. From within the corridor, the prisoner can see nothing but the corridor itself curving off and the doors to the cells on the outer wall.
Addendum 3:
3a. Please note new disclaimer additions #13 and #14.
3b. If this riddle is too long due to all the disclaimers then don't tell me, tell Nigel_Parsons  . (It's cool, Nigel, I'm just playing, keep sending your solutions!)
Addendum 4: (Compliments of Leonid Broukhis)
Quote:| 4a. The prisoner does not have access to any measuring equipment, and he does not need any, because the width of the corridor happens to be equal to the distance between doors + the door width. |
|
|
| « Last Edit: Jul 20th, 2004, 5:20pm by mattian » |
 IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
 |
Re: A Prisoner & 100 light bulbs
« Reply #1 on: Jul 16th, 2004, 11:27am » |
 Quote  Modify
|
Some initial thoughts:
::
1) The prisoner cannot get any information from his first visit to a cell.
2) The only information potentially gained by toggling the bulb in a previously unvisited cell is that the switch doesn't control the light in any previously visited cell.
3) If the initial state is known, a binary approach will solve the problem with absolute certainty in O(n log n) visits to cells.
4) Due to the circular nature of the prison, determining the number of cells (assuming the prisoner can't measure the angle between successive cells or otherwise derive the number of cells - eg by tracking his orientation or by somehow recognising a specific cell) is going to be the meat of the problem, and will probably automatically solve most of the switch identification as well...
::
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #2 on: Jul 16th, 2004, 12:00pm » |
Quote Modify
|
Note:
1. The prisoner does not have access to any measuring equipment.
2. It is safe to assume that all cells may be visited in reasonable (finite) time. For the purpose of keeping this within scope, let us assume that the number of cells does not exceed 1000 (and the prisoner knows this).
Responses to your initial comments.
::
1. Agreed.
2. Could you rephrase this statement making careful distinctions between toggling the button vs. toggling the bulb.
3. Agreed - although it should be noted that to switch any bulb on and observe it will require between 1 and 2 visits. I believe - using the most straight forward approach, given that the bulbs were all initially off - it would take closer to but not quite O(2n log n).
4. The prisoner does not have access to any measuring equipment. And yes - I believe that knowing the number of cells is a big piece of the puzzle.
::
|
| « Last Edit: Jul 16th, 2004, 12:09pm by mattian » |
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: A Prisoner & 100 light bulbs
« Reply #3 on: Jul 16th, 2004, 4:59pm » |
Quote Modify
|
Knowing the number of cells is easy:
::
Find a cell (X) in which a button controls some other cell.
S = bulb{X];
left = -1; rigth = -1; done = false;
For i = 1 step 1 until done do begin
if (left == -1) {
Go i cells to the left, press a button there.
Return to X
if S != bulb[X] then {
left = i;
if right != -1 then total = left + right; done = true
S = bulb[X]
}
}
if (right == -1) {
Go i cells to the right, press a button there
Return to X
if S != bulb[X] then {
right = i;
if left != -1 then total = left + right; done = true
S = bulb[X]
}
}
end for
::
Using C notation to avoid visible math symbols
|
| « Last Edit: Jul 16th, 2004, 5:06pm by Leo Broukhis » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #5 on: Jul 16th, 2004, 6:54pm » |
Quote Modify
|
Hey Leonid
First of all, while I agree that your method for determining how many cells there are will work, it isn't optimal. But, since I asked two questions in the riddle, first to establish a working strategy and then optimize, I will be satisfied with the first solution first and the second second.
Secondly, to answer your question. If the prisoner correctly establishes the number of cells, it is easy for him to assign labels to the cells as you did in your example. The only reason why label assignments would be meaningless to the guards would be in the case where the number of cells were unknown.
So by simply beginning his explanation to the guards by saying, there are n cells let the this one over here be labeled cell #1 and all subsequent cells up to cell n labeled sequentially, here is my solution.
|
|
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: A Prisoner & 100 light bulbs
« Reply #6 on: Jul 16th, 2004, 7:20pm » |
Quote Modify
|
mattian,
If the prisoner never passes a cell without looking into it then he can infer all edges in the connectivity graph except ones that have, roughly, positive scalar product with the vector from X to the X-controlling cell). Then the prisoner will have to repeat the process starting from the X-controlling cell,
skipping known cells.
My question about cell labeling was because I thought that after the prisoner claims that he has the solution he could be brought (teleported) into an interrogation room and therefore he could lose the reference point.
|
| « Last Edit: Jul 16th, 2004, 7:26pm by Leo Broukhis » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #7 on: Jul 16th, 2004, 7:30pm » |
Quote Modify
|
Leonid,
While I'm sure you're correct, I admit I don't fully understand your statement. Are you saying:
::
... that a prisoner starting at arbitrary cell x (which controls the bulb in cell y) can visit each cell sequentially to find cell y after pushing the button in cell x, and then move onto cell (x+1) and repeat the process?
::
Addendum:
Sorry Leonid, I missed your point about losing the reference point. You are correct, in my original problem statement I did not specify how he might explain the solution to the prison guards without being able to directly reference an arbitrary door by pointing at it, for example. Perhaps a clean way of handling this is to make the prisoner send the signal to the guards that he knows the solution by switching all the lights off, and then switching them all on sequentially (such that the lights are sequential not the button pushin) until they're all on. But unfortunately this would allow the prisoner to guess the solution - which is not allowed. I will clarify this issue somehow in the problem statement.
|
| « Last Edit: Jul 16th, 2004, 9:16pm by mattian » |
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: A Prisoner & 100 light bulbs
« Reply #8 on: Jul 16th, 2004, 7:43pm » |
Quote Modify
|
No need to hide anymore, I think.
No, it's the other way around. The main point is to press a different button at every pass. Consider a (potentially infinite) line of cells. Assume cell 0 does not control itself. Then the prisoner starts diverging sweeping movements looking at every cell every time and only pressing the button in rooms he has not visited before. This way he can infer all edges (a, b) where abs(a) > abs(b) and half of abs(a) == abs(b) depending on which way he went first.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #9 on: Jul 16th, 2004, 9:07pm » |
Quote Modify
|
Indeed - the solution is quite trivial if you know the number of cells, as was that for the original "100 prisoners and the single light bulb in the switch room" puzzle. The optimal solution, however, is not as simple.
I will write your solution into my simulation and post the results - or you can  .
|
| « Last Edit: Jul 16th, 2004, 9:10pm by mattian » |
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: A Prisoner & 100 light bulbs
« Reply #10 on: Jul 17th, 2004, 8:30am » |
Quote Modify
|
on Jul 16th, 2004, 12:00pm, mattian wrote:
Responses to your initial comments.
[...]
2. Could you rephrase this statement making careful distinctions between toggling the button vs. toggling the bulb.
|
|
The only information potentially gained by toggling the bulb in a previously unvisited cell is that the switch which controls it doesn't control the light in any previously visited cell.
Quote:
3. Agreed - although it should be noted that to switch any bulb on and observe it will require between 1 and 2 visits. I believe - using the most straight forward approach, given that the bulbs were all initially off - it would take closer to but not quite O(2n log n).
|
|
I got (without dynamic optimisations like observing a toggled bulb during a switching pass) 1.5n [lciel]log2 n[rciel] - each stage consists of 2 passes, the first visiting n/2 cells and toggling their switches, and the second visiting all cells to determine the new state. It then requires [lciel]log2 n[rciel] stages to identify each switch with certainty. Of course, there are some trivial optimisations - for instance you will always know the state of the bulb in the cell with the last switch and the bulb in the last cell visited in the second pass of each stage before you go in. And, of course, it's possible to adjust your strategy on the fly to account for cells that control their own light, and cells that are controlled by a switch toggled earlier in the current first pass of a stage.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #11 on: Jul 18th, 2004, 10:40am » |
Quote Modify
|
Quote:| The only information potentially gained by toggling the bulb in a previously unvisited cell is that the switch which controls it doesn't control the light in any previously visited cell. |
|
I assume you mean that this determination can be made if previously visited cells are revisited. The reason I had trouble accepting your statement is best illustrated in an example:
Five cells - {A, B, C, D, E}
If you've visited A, B and C and you toggle the switch in C (which happens to control E), no such determination (as your statement suggests) can be made without first revisiting A, B and C. Is that right?
|
| « Last Edit: Jul 18th, 2004, 10:45am by mattian » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #12 on: Jul 18th, 2004, 10:57am » |
Quote Modify
|
Here are some of my thoughts about this problem:
One of the things I liked about it was that to truly optimise the solution, one is forced to employ different techniques for the different stages of the problem. There is no one-concept-fixes-all solution.
For instance, as RMS mentioned in the beginning, establishing the size of the prison is one of the important steps. this process can be optimised independently - or in fact, as part of one of the other processes.
While Leonid's solution to this portion of the problem will work it should probably be done at the same time that some reverse engineering on the wiring is done. Although I think an accurate knowledge of the size of the prison is less important in the beginning than it is later on.
There is a solution which uses no visits for this phase of the puzzle, but the result is resolved over time rather than being absolute in the beginning.
I have a simulation for this problem running at the moment and I will post results to this thread soon. I will also include results from the most basic strategies mentioned and those suggested as potential optimisations.
|
| « Last Edit: Jul 18th, 2004, 11:01am by mattian » |
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
Gender:
Posts: 2873
|
|
Re: A Prisoner & 100 light bulbs
« Reply #13 on: Jul 19th, 2004, 4:14am » |
Quote Modify
|
on Jul 18th, 2004, 10:40am, mattian wrote:
I assume you mean that this determination can be made if previously visited cells are revisited. The reason I had trouble accepting your statement is best illustrated in an example:
Five cells - {A, B, C, D, E}
If you've visited A, B and C and you toggle the switch in C (which happens to control E), no such determination (as your statement suggests) can be made without first revisiting A, B and C. Is that right? |
|
I mean that the only deduction you can possibly make, whatever future actions you take, is that the switch controls a light in some unspecified room you hadn't previously visited - in your example, by subsequently visiting all the cells, you can conclude that the switch in C controls the bulb in either D or E, but not which...
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #14 on: Jul 19th, 2004, 5:34am » |
Quote Modify
|
Okay - I see what you mean. You're saying that at any time, you are free to determine (through whatever means) that a switch either controls a light in a room that you've visited, or it doesn't. If it does, then you know which room it controls - if it doesn't, then you don't know which of the unvisited rooms it controls. Agreed.
|
|
IP Logged |
|
|
|
Nigel_Parsons
Junior Member
Gender:
Posts: 63
|
|
Re: A Prisoner & 100 light bulbs
« Reply #15 on: Jul 19th, 2004, 11:11am » |
Quote Modify
|
Looking for a ‘simple’ solution, within the bounds of the question.
We require:
Question 1 - What strategy can the prisoner employ to guarantee his freedom?
Question 2 - How can the prisoner minimize the number of cell visits he needs to make before he can declare the solution?
We know:
8. Despite any efforts he might make, the prisoner can not extract any positional state information from the button - it always looks the same.
9. All operations on the button must be performed from within the respective cell with the door closed.
10. No information from the outside world will be available to the prisoner when he is inside a cell - the only information available to him from within the cell, is the state of the light bulb in that cell, and what he decides to do with the button (if anything).
It would seem the first action is to do a full round of the corridor, opening all cell doors to see if the cells are illuminated. Clearly this would be visible from the corridor, as the only time a door needs to be closed is to perform an operation on a button.
Whilst doing the rounds, note the sequence of on/off bulbs. Hopefully this will identify a unique sequence of rooms at some point in the tour. (this is the problem which may make the solution longer)
If a unique sequence has been identified, a mental map of all rooms can be made. Starting at an identifiable point (clockwise end of unique sequence?) do one more round trip. When you return to the known point you will know the total number of rooms. (second problem, all the rooms may form 2 or more identical sequences of rooms so you still do not know for certain that you know the number of rooms!)
At this stage you have not ‘visited’ a single room, thus helping with Q2.
Enter one room & toggle the switch.
Leave the room (leaving the door open) and do another tour of the corridor comparing the illuminations with your mental map. (at this stage you can confirm the total number of rooms as in repeated sequences only one difference in illumination will show)
You now know the number of rooms and the correlation between one switch and one bulb.
Now enter each room in turn, toggling its switch and then doing a full tour of the corridor.
For N rooms you will need to enter N-1 to get the full picture (the last switch/bulb can be identified by elimination), but you may be tired from the repeated tours of the corridor.
Even if you are transported out to make your report you can identify the sequence by switching the last switch. This will restore the ‘unique’ sequence you found earlier, only each light will have been toggled once.
The only problem which will increase the number of visits required is if no ‘unique’ pattern appears on your first tour. You will then need to toggle sufficient switches to present a unique pattern. I leave that part of the problem to the next man (for now)
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #16 on: Jul 19th, 2004, 11:44am » |
Quote Modify
|
Hey Nigel,
If you've proved anything it is that despite all efforts on the part of a riddle author (or in my case, part plagiariser), loopholes will be found which will undermine the fundamental principles originally scoped for the riddle's solution. However, since your solution did not mention the phrases, "kill the guards, steal the key," I will forgive you your outside-the-box-yet-within-question-limitations solution and provide you with a sincere response. Frankly I welcome the interest and have no desire to alienate the few people who show interest.
First of all, you did seem to miss the all encompassing disclaimer:
Quote:| 12. If you think you have an answer which solves the problem using some trivial "kill the guards, steal the key" solution which doesn't contradict any of the limitations of this puzzle, then this statement says you're wrong. |
|
This basically means you're not allowed to be creative and find gaps in the wording through which you can squeeze a solution. But again, it could be argued that your solution is not a "kill the guards, steal the key" solution and so I will be forced to add another disclaimer to the puzzle which states:
"13. If your name is Nigel_Parsons, your solution is wrong."
But, moving on...
While writing the riddle, I had the intention of including the disclaimer that doors close automatically, and faster than the prisoner can move from one cell to another. There are no gaps around the door through which light can pass. From the corridor, the prisoner can see the state of only one bulb at a time - when he is entering or leaving a room. Observing the state of a bulb counts as a visit.
I will add this to the problem statement.
But, moving on still...
::
Your mental map of the sequence is a good solution which ties in with my own. This does eliminate the need to visit cells simply to count them. However, the problem you mentioned regarding aliasing (or partial sequences interfering with the prisoner's ability to accurately discern the complete sequence) can be solved quite easily before any rooms are visited at all.
::
Given my obviously poor original phrasing of the puzzle, your solution makes sense. However, I, being the God of this riddle, have now modified the constraints and applied - most importantly - disclaimer #13.
Thanks
|
| « Last Edit: Jul 19th, 2004, 11:48am by mattian » |
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: A Prisoner & 100 light bulbs
« Reply #17 on: Jul 19th, 2004, 3:48pm » |
Quote Modify
|
I believe that the Nigel's solution is limited to cases where the initial state of the bulbs is unique wrt rotations. But even then, without doing a sweeping movement you can never be sure if a room you've going into is a completely new one that happens to match your expectation of what would be a result of your pressing a button somewhere else, or a room that you've seen already and that has indeed changed its illumination state.
[e] A typo.
|
| « Last Edit: Jul 19th, 2004, 3:49pm by Leo Broukhis » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #18 on: Jul 19th, 2004, 4:59pm » |
Quote Modify
|
I agree with Leonid, however, the principle that Nigel used does form part of a solution which can establish the number of cells in an average of 10 visits. However, his solution alone is not sufficient to do this.
|
|
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: A Prisoner & 100 light bulbs
« Reply #19 on: Jul 19th, 2004, 6:00pm » |
Quote Modify
|
on Jul 19th, 2004, 4:59pm, mattian wrote:| I agree with Leonid, however, the principle that Nigel used does form part of a solution which can establish the number of cells in an average of 10 visits. However, his solution alone is not sufficient to do this. |
|
In an average of 10 visits to every cell, you mean? Is it for the potentially unbounded number of rooms, or for a number that is of the same order of binary magnitude as 1000?
As an improvement of my algorithm to find the number of rooms, I can suggest the sweeping movements of exponentially increasing depth (toggle 1 room to the left; 2 to the right; 4 to the left after skipping 1; 8 to the right after skipping 2, etc..., and a binary search afterwards. Requires visiting more rooms, but much less walking.
I'm contemplating a binary search of another kind: after establishing the number of rooms, do a round toggling every other room; observe results; then toggling every two rooms out of 4, etc. The the set of numbers of passes when the light in a room changed state gives you the number of the controlling room. I do not see who how to combine this pass with the pass to find out the number of rooms, though.
|
| « Last Edit: Jul 19th, 2004, 6:07pm by Leo Broukhis » |
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #20 on: Jul 19th, 2004, 6:40pm » |
Quote Modify
|
Quote:| In an average of 10 visits to every cell, you mean? |
|
Actually, no. I mean 10 visits total. - for a prison of about 100 cells. Although 1000 cells wouldn't much increase the number visits used to count the cells.
You make another good point about unbounded numbers of cells which is why I modified the riddle to keep numbers within managable maxima. My solution would suffer from practical limitations for exceedingly large numbers of total prison cells.
My solution has two parts - the first establishes the number of cells as an extremely accurate approximation. The second phase is the reverse engineering process which doubles as verification for the initial cell count.
In the example of 100 cells, 10 visits on average is enough to determine the number of cells in the prison - it could be done in fewer with higher risk of error, but 10 is a relatively small number in contrast to the complete solution.
Your method of switching every second, and then every third and forth, and so on is very close to my first solution - and in fact my current solution is built on that premise.
I would be very interested to see some simulation results for examples involving 100 cells. I'm holding out with my numbers because I myself am not yet satisfied with my own results - I promise to post the benchmark by the end of the week.
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #21 on: Jul 19th, 2004, 7:03pm » |
Quote Modify
|
A few more notes:
I have not yet had time to attempt the various strategies I've considered for this problem. My current solution seems fairly good although I have to rely on my own logical interpretation of why it should be a good solution. Only the numbers can tell us if it is or not.
Secondly, I should mention that I made a big mistake by creating a puzzle that would attract geniuses like RMS and Leonid - I have to omit Nigel for disclaimer abuse. The problem is that the responses I'm getting here are far too difficult for me to understand so I end up blabbering responses to you while trying to sound like I know what I'm talking about - so bear with me.
Also, although my method for counting the rooms is fairly cheap, it constitutes such a small percentage of the complete solution that it hardly seems worth it. However, if you don't manage to count the cells cheaply, I suppose it would have a higher percentage contribution, so I suppose it is justified after all.
Finally, I'm not keeping my solution to myself to be an annoying secret bearer - like a giddly little school-girl's, "I got a secret, nyah, nyah, nyah," mentality - I just don't want to corrupt your thought processes.
|
| « Last Edit: Jul 19th, 2004, 7:06pm by mattian » |
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: A Prisoner & 100 light bulbs
« Reply #22 on: Jul 19th, 2004, 7:21pm » |
Quote Modify
|
on Jul 19th, 2004, 6:40pm, mattian wrote:
Actually, no. I mean 10 visits total. - for a prison of about 100 cells. Although 1000 cells wouldn't much increase the number visits used to count the cells.
|
|
Does the prisoner need to know the approximate number of cells (within
+/- constant or within an order of magnitude?), or the guaranteed upper bound? Would your algorithm work if there are, say, 103 cells, but the prisoner is told that there are around 100?
Quote:
In the example of 100 cells, 10 visits on average is enough to determine the number of cells in the prison - it could be done in fewer with higher risk of error, but 10 is a relatively small number in contrast to the complete solution.
|
|
Either I have a mental block switching from the unbounded number of cells to a limited number, or there is something wrong with that algorithm. Suppose there are exactly 100 cells. How many visits do you need to prove that there are exactly 100 cells?
|
|
IP Logged |
|
|
|
mattian
Senior Riddler
Gender:
Posts: 404
|
|
Re: A Prisoner & 100 light bulbs
« Reply #23 on: Jul 19th, 2004, 8:05pm » |
Quote Modify
|
Quote:| Does the prisoner need to know the approximate number of cells (within +/- constant or within an order of magnitude?), or the guaranteed upper bound? Would your algorithm work if there are, say, 103 cells, but the prisoner is told that there are around 100? |
|
The prisoner would have to know the approximate number of cells before resolving to a definite number - but he wouldn't have to be told - he could establish it on his own.
Quote:| Either I have a mental block switching from the unbounded number of cells to a limited number, or there is something wrong with that algorithm. Suppose there are exactly 100 cells. How many visits do you need to prove that there are exactly 100 cells? |
|
The limited number of cells is definitely significant and different from the unbounded case - for practical reasons. I established a context for this riddle which allows solvers of it to use manageable numbers.
Had I posed the original puzzle as the original prisoner-lightbulb problem was posed, by saying there are exactly 100 cells then I doubt the significance of the number would be questioned. However, I left it open to the general case but included a limitation which kept the number within the grasp of a practical solution.
There are properties of the prison which become hazy as the number of cells becomes too large.
Quote:| How many visits do you need to prove that there are exactly 100 cells? |
|
Unfortunately this question can not be answered with a number. It depends on the distribution of light bulb status. The more 'ambiguous' the distribution, the more visits will be necessary - but this can be determined on the fly. After visiting an average of 10 cells, the prisoner will know the exact number of cells - guaranteed. But the number 10 is not guaranteed - it's a guaranteed average, for accurate results.
It's difficult not to be cryptic - sorry about that.
|
|
IP Logged |
|
|
|
Leo Broukhis
Senior Riddler
Gender:
Posts: 459
|
|
Re: A Prisoner & 100 light bulbs
« Reply #24 on: Jul 19th, 2004, 11:53pm » |
Quote Modify
|
on Jul 19th, 2004, 8:05pm, mattian wrote:
Unfortunately this question can not be answered with a number. It depends on the distribution of light bulb status. The more 'ambiguous' the distribution, the more visits will be necessary - but this can be determined on the fly.
|
|
But the answer to my question does have a numerical answer. It is the number of visits that is sufficient to determine the number of rooms under the worst conditions.
Quote:
After visiting an average of 10 cells, the prisoner will know the exact number of cells - guaranteed. But the number 10 is not guaranteed - it's a guaranteed average, for accurate results.
|
|
If 10 is the average, the what is the minimum and what are the conditions to achieve it? My feeling is that there is a flaw somewhere. We can play a game: I'll generate a graph with 90+random(20) nodes and randomly assign the starting values of bulbs. Then, without loss of generality, I'll pick a node ant tell you whether it is light or dark there (this vill be visit #1). Then you tell me what to do. Are you game?
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print