Author |
Topic: Denesting Nested Radicals (Read 3315 times) |
|
Barukh
Uberpuzzler
Gender: 
Posts: 2276
|
Simplify the following doubly nested radicals to a combinations of singly nested radicals (and thanks towr for his amazing formula generator!  )
P.S. The usual question: Does it belong to the hard section? Not all the expressions are hard, but I believe some of them are.
|
| « Last Edit: Dec 29th, 2003, 5:12am by Barukh » |
 IP Logged |
|
|
|
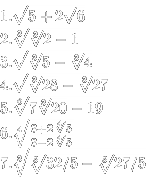
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
 |
Re: Denesting Nested Radicals
« Reply #1 on: Dec 29th, 2003, 7:28am » |
 Quote  Modify
|
::
1) sqrt(3)+sqrt(2)
6) 5^(3/4)/2 + 5^(1/4)/2 + sqrt(5)/2 + 3/2
::
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Denesting Nested Radicals
« Reply #3 on: Dec 29th, 2003, 8:40am » |
Quote Modify
|
towr, so far so good ! Although 6) also has a nicer looking expression.
I am curious: how do you get the answers?
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Denesting Nested Radicals
« Reply #4 on: Dec 29th, 2003, 9:26am » |
Quote Modify
|
I'm mostly just trying things out in my math program, the first one rolled out immediately, the other two took a bit more work.
In 6 I just tried to work out the denominator, by multiplying numerator and denominator with first (3+2(5)^(1/4)) and then (9 + 4 sqrt(5)). After that my mathprogram simplified it further..
#4 took most work from my part..
sqrt(28^(1/3) - 3) = x
(28^(1/3) - 3) = x^2
x^6 + 9·x^4 + 27·x^2 + 27 = 28
(x^3 + x^2 + 5·x - 1)·(x^3 - x^2 + 5·x + 1) = 0
solving the first factor then gives the answer (though I wouldn't know how to do that without my trusty math program either..)
http://mathforum.org/library/drmath/view/52657.html
http://mathforum.org/library/drmath/view/52660.html
helped a bit as well..
I wish I could find some better tools to solve these kind of problems though..
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Denesting Nested Radicals
« Reply #5 on: Dec 30th, 2003, 12:36pm » |
Quote Modify
|
Quote:Although 6) also has a nicer looking expression.
|
|
6) (51/4 + 1)/(51/4 - 1)
Surprisingly, 5) has a simpler answer than 2).
|
| « Last Edit: Dec 30th, 2003, 11:46pm by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: Denesting Nested Radicals
« Reply #6 on: Jan 13th, 2004, 4:43am » |
Quote Modify
|
Is it possible to give any hints or clues for the above problems (except maybe the first one!!) 
|
|
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Denesting Nested Radicals
« Reply #7 on: Jan 14th, 2004, 1:28am » |
Quote Modify
|
on Jan 13th, 2004, 4:43am, TenaliRaman wrote:| Is it possible to give any hints or clues for the above problems (except maybe the first one!!) |
|
Here are some hints (I try not to give in too much – please ask for more if you need):
[sqrt]- Start with 6). The answer will have the same form: it’s a fraction  , and the numerator is a1/4 + b1/4.
Then try 5). As THUD&BLUNDER said, it has a simple form – namely, it’s a linear combination of two terms.
All the other cases may be represented as a linear combination of 3 terms -[sqrt].
Unfortunately, an algorithm for denesting radicals in the general case is still unknown (or is it fortunately?), so don’t get disappointed. The radicals presented here (except the first one) are due Ramanujan who gave just the answers, not the explanations of the solutions.
|
| « Last Edit: Jan 14th, 2004, 1:30am by Barukh » |
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Denesting Nested Radicals
« Reply #8 on: Jan 14th, 2004, 1:32am » |
Quote Modify
|
on Dec 30th, 2003, 12:36pm, THUDandBLUNDER wrote:| Surprisingly, 5) has a simpler answer than 2). |
|
Correct. Do you know the answers to all the cases?
|
|
IP Logged |
|
|
|
John_Gaughan
Uberpuzzler
Behold, the power of cheese!
    
 
Gender:
Posts: 767
|
|
Re: Denesting Nested Radicals
« Reply #9 on: Jan 14th, 2004, 6:59am » |
Quote Modify
|
Powers and radicals like these fascinate me, but I am unlearned in this corner of math. Could someone please explain how they get their answers? I made it as far as calculus and discrete math in college, so please don't confuse me too much
|
|
IP Logged |
x = (0x2B | ~0x2B)
x == the_question
|
|
|
TenaliRaman
Uberpuzzler
I am no special. I am only passionately curious.
Gender:
Posts: 1001
|
|
Re: Denesting Nested Radicals
« Reply #10 on: Jan 14th, 2004, 10:43am » |
Quote Modify
|
Yeeehaw!!!!!!!!!!!!!!!
ok i haven't solved 6 yet!
But i have solved 3 and if my hunch is right i have a method for 4 as well.
I will hide the answer for 3 but i am not hiding the method i used to solve it.
Ok,
first of all lets look at a general expression,
sqrt(1-cubrt(b/a)) with a>b
let me write b/a as w so w<1 and our general expression is,
sqrt(1-cubrt(w))
expand this binomially and soon it will be noticed that we have a period 3 cycle which implies that, i can write
sqrt(1-cubrt(w)) = x + y*cubrt(w) + z*cubrt(w2) .... (*)
(provided x,y and z are finite converging limits .. i am assuming it for now)
I can see 2 methods for getting x,y and z,
method 1>
Enumerate the series which equals to x , series which equals to y and series which equals to z. If it is possible to find the value of the series then we would have found x,y and z.
method 2>
square both sides of (*) and equate the coefficients of 1,w and w2 and solve the simultaneous equation. (This gets pretty tedious and i used this to do third question and it took me pretty long time.)
The above method can be used to solve the 4th question as well.
Answer to 3rd :
::(1/3)*(cubrt(2)+cubrt(20)-cubrt(25))
Note: If you see 25 = 5^2, 20 =5*4
25 = 25/16 * 16 = (5/4)^2 * 16
20 = (5/4) * 16
2 = (2/16) * 16
It seems there is a pattern running here which means a generalised solution for sqrt(1-cubrt(w)) is possible given some convergence conditions.::
[edit]
Giving it some more thought,
this idea will work for any nthroot(1-cubrt(w)), since each one of this will be a period 3 cycle. It is just that evaluating x,y and z will become hectic. That's not very encouraging to me (however this implies we can solve 2 by this method)
Also, nthroot(1-mthroot(w)) will be a period m cycle , so we will have m variables. This implies this could be used to solve 7th as well ,only problem is that we will have 5 variables to contemplate with!! phew!!
[/edit]
All that is left now is 6 and 5.
|
| « Last Edit: Jan 14th, 2004, 11:20am by TenaliRaman » |
IP Logged |
Self discovery comes when a man measures himself against an obstacle - Antoine de Saint Exupery
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Denesting Nested Radicals
« Reply #11 on: Jan 15th, 2004, 1:11pm » |
Quote Modify
|
Quote:Giving it some more thought,
this idea will work for any nthroot(1-cubrt(w)), |
|
TenaliRaman, for 3) there is a solution to [smiley=surd.gif](3[smiley=surd.gif]a + 3[smiley=surd.gif]b) iff there exist integers p,q such that
a = (4p + q)q3
b = 4(p - 2q)p3
In which case,
[smiley=surd.gif](3[smiley=surd.gif]a + 3[smiley=surd.gif]b) = [smiley=pm.gif][{3[smiley=surd.gif]2(p - 2q)2} - {3[smiley=surd.gif](4p + q)2} - {3[smiley=surd.gif]4(p - 2q)(4p + q)}]/3
For [smiley=surd.gif](3[smiley=surd.gif]5 - 3[smiley=surd.gif]4), p = q = 1 and the result easily follows.
Finding p,q in general, given they exist, is not easy and requires some familiarity with Galois field theory. 
But the above assumes that neither a nor b are zero and that a/b is not a cube in [smiley=bbq.gif].
That is, a/b does not equal c3 for any c in [smiley=bfcq.gif].
If c [smiley=in.gif] [smiley=bbq.gif] and a/b = c3 then [smiley=surd.gif](3[smiley=surd.gif]a + 3[smiley=surd.gif]b) = 6[smiley=surd.gif]b[smiley=surd.gif](c + 1)
Unfortunately, we cannot use this form to solve 5) as 20 is not a perfect cube.
For some reason (to do with the expressions for a and b not being relatively prime for certain p,q),
we sometimes need to swap them around and have
a = 4(p - 2q)p3
b = (4p + q)q3
Applying this form to 4), where a = 28 and b = -27, we get p = -1 and q = 3.
This gives [smiley=surd.gif](3[smiley=surd.gif]28 - 3[smiley=surd.gif]27) = [smiley=pm.gif](3[smiley=surd.gif]98 - 3[smiley=surd.gif]28 - 1)/3
(The above formulae are due to Ramanujan.)
============================================
A simple method for 1)
5 + 2[smiley=surd.gif]6 = (10 + 4[smiley=surd.gif]6)/2 = (2 + [smiley=surd.gif]6)2/2
So [smiley=surd.gif](5 + 2[smiley=surd.gif]6) = [smiley=pm.gif](2 + [smiley=surd.gif]6)/[smiley=surd.gif]2 = [smiley=pm.gif]([smiley=surd.gif]2 + [smiley=surd.gif]3)
|
| « Last Edit: Jan 25th, 2005, 7:06am by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Denesting Nested Radicals
« Reply #12 on: Jan 15th, 2004, 5:34pm » |
Quote Modify
|
For 2) cbrt( cbrt(2)-1) = ( cbrt(3)-cbrt(6)+cbrt(12) )/3
Solution method: Tried to write cbrt(2)-1 as the cube of something. After failing to find a two term expression that worked, tried a three term expression, which I assumed would have the form
A + B*2^(1/3) + C*2^(2/3)
under the assumption that constants A, B, C could be chosen to zero out any 2^(2/3) term. That left equations for A, B, and C, which weren't difficult to solve since it turned out that A=C=-B=9^(-1/3). Then rearranged to get the 9^(1/3) out of the denominator.
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Denesting Nested Radicals
« Reply #13 on: Mar 21st, 2004, 1:29am » |
Quote Modify
|
Solve [smiley=surd.gif][x - 2[smiley=surd.gif](x-1)] + [smiley=surd.gif][x + 2[smiley=surd.gif](x-1)] = 1/(x-1)
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Denesting Nested Radicals
« Reply #14 on: Mar 21st, 2004, 6:35am » |
Quote Modify
|
on Mar 21st, 2004, 1:29am, THUDandBLUNDER wrote:| Solve [smiley=surd.gif][x - 2[smiley=surd.gif](x-1)] + [smiley=surd.gif][x + 2[smiley=surd.gif](x-1)] = 1/(x-1) |
|
Are we looking at the real solutions?
[smiley=blacksquare.gif]1.5[smiley=blacksquare.gif]
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print