Author |
Topic: Perfect Square (Read 1786 times) |
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender: 
Posts: 4489
|
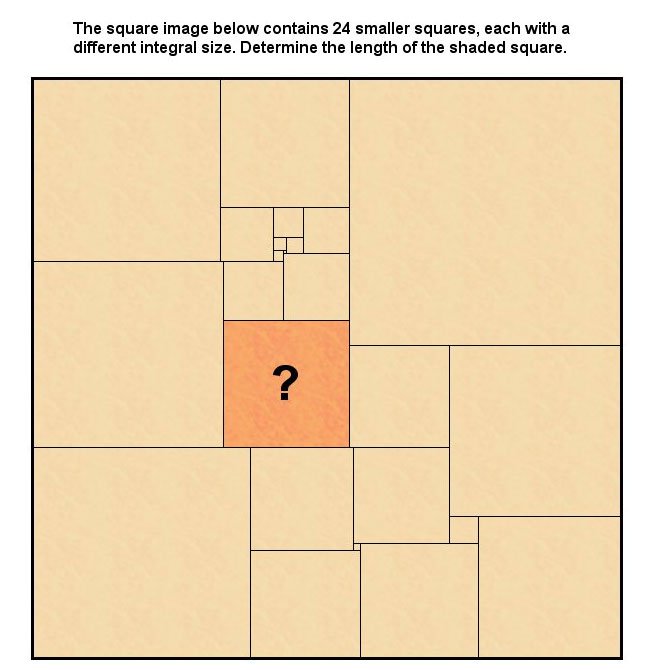
Find the shaded area.
|
| « Last Edit: Nov 5th, 2003, 6:34am by ThudnBlunder » |
 IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
 |
Re: Squares
« Reply #1 on: Nov 5th, 2003, 5:51am » |
 Quote  Modify
|
My first intuition is to assign each side a variable, and solve it using gaussian elimination fluff 
[e]actually, there isn't a unique solution, since any integral multiple of the collection of squares would have the same properties.
But I suppose we can choose the smallest possible value[/e]
|
| « Last Edit: Nov 5th, 2003, 6:04am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
visitor
Guest
|
The square can be solved in two parts. First, the upper left hand corner forms a self-contained rectangle that is easily solved to give the mystery square a size of 38, when the smallest square (call it z) is 1. The rectangle then has dimensions of 94 by 111. Plug that into the whole image. If I assign x to the smallest of the remaining boxes and y to the box right above it, I end up with 41x+y=111z. and 4y-11x=94z. And because it's a square, you can also equate 26x+y+94z=3x+2y+111z. So z=1, x=2, and y=29. And the mystery square retains its size of 38.
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
Well done, visitor.
Now that you have the hang of it, what's the area of the large square in the top left-hand corner?
|
| « Last Edit: Dec 11th, 2003, 4:06pm by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Perfect Square
« Reply #4 on: Dec 10th, 2003, 3:10pm » |
Quote Modify
|
Is the whole thing still a square?
|
|
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Perfect Square
« Reply #5 on: Dec 10th, 2003, 5:55pm » |
Quote Modify
|
Quote:| Is the whole thing still a square? |
|
Yes, just as in the first puzzle.
|
|
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
|
Re: Perfect Square
« Reply #6 on: Dec 11th, 2003, 11:43am » |
Quote Modify
|
OK, I think I know the answer: [smiley=blacksquare.gif]50[smiley=blacksquare.gif].
The solution will follow...
|
|
IP Logged |
|
|
|
Barukh
Uberpuzzler
Gender:
Posts: 2276
|
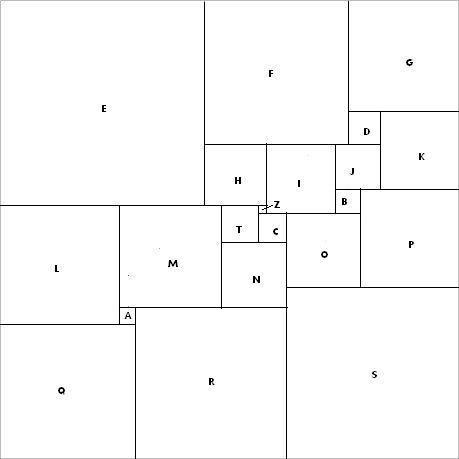
Here's the solution:
[smiley=blacksquare.gif]
First, I made an assumption – based on the relative sizes of squares – that Z < A < B < C < D.
I began by choosing Z, A, C as “independent” quantities. Then, we have T = C+Z, N=2C+Z, M = 3C+2Z etc. Closing on R, I got the following relation: 4A = 2C+Z, which showed that Z must be even. So, the smallest possible assignment is Z=2, A=3, C=5.
Next, I turned to the right-bottom part of the big square. Since S = 2*O+B = R+N+C-O, I get 3*O+B = 6C+3Z+3A, that is, B is a multiple of 3. This eliminates the aforementioned assignment for A and C, so I considered the next possibility A=4, C=7. Then, B=6, O=18, P=24, S=42, and the size of the big square is 112.
Finally, 2J+D = P+B = 30, and K+G = 2J+3D = 46, so D=8, J=11. The requirements of the problem (each square being of unique size) are fulfilled, and also are the assumptions. The rest is really straightforward.
[smiley=blacksquare.gif]
|
| « Last Edit: Dec 11th, 2003, 2:27pm by Barukh » |
IP Logged |
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
|
Re: Perfect Square
« Reply #8 on: Dec 11th, 2003, 7:45pm » |
Quote Modify
|
Well done, Barukh. 
With all due respect, this puzzle is obviously not as difficult as I had assumed and moderators may feel free to move it where they think fit.
But finding such squares from scratch is difficult.
See, for example, http://mathworld.wolfram.com/PerfectSquareDissection.html
|
| « Last Edit: Dec 11th, 2003, 8:03pm by ThudnBlunder » |
IP Logged |
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print
Remove