Author |
Topic: Combinations of Pi and Sqrt(2) (Read 22062 times) |
|
william wu
wu::riddles Administrator
Gender: 
Posts: 1291
|
 |
Combinations of Pi and Sqrt(2)
« on: Oct 15th, 2003, 9:06pm » |
 Quote  Modify
|
Say I am given a number X = A*[sqrt]2 + B*[pi], where A and B are integers.
Given X, how can you find A and B, without using brute force?
|
| « Last Edit: Oct 15th, 2003, 9:06pm by william wu » |
 IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #1 on: Oct 15th, 2003, 9:19pm » |
Quote Modify
|
Some of my initial ideas:
My immediate intuition was dot products, because whenever I see a function which is a linear combination of basis functions, I know I can take the dot product of the function with each basis function to get the coefficients of the linear combination. However, these are integral coefficients, and it doesn't make sense to say [pi] and [sqrt]2 are orthogonal functions.
[pi] cannot be expressed as a rational multiple of [sqrt]2. So there is only one possible solution, if any.
Is it true that for any [epsilon] > 0, [exists] integers A and B such that [epsilon] = A[pi] + B[sqrt]2? How to prove/disprove this? If it is true, then perhaps we can argue that the problem is uncomputable, because finding a solution would require infinite precision computations, and thus infinite time/space.
If however we restrict A and B to be positive integers, then all I can think of is the knapsack algorithm, which runs in psuedopolynomial time. Perhaps there are some mathematical properties of sqrt(2) vs. [pi] that I can bank on to get a faster solution?
|
|
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Rezyk
Junior Member
Gender:
Posts: 85
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #2 on: Oct 15th, 2003, 10:12pm » |
Quote Modify
|
on Oct 15th, 2003, 9:19pm, william wu wrote:Is it true that for any [epsilon] > 0, [exists] integers A and B such that [epsilon] = A[pi] + B[sqrt]2? How to prove/disprove this?
It fails for any rational epsilon; proof by contradiction:
Let [epsilon] = p/q (p, q integers) = A[pi] + B[sqrt]2.
=> Aq[pi]+Bq[sqrt]2 - p = 0.
=> [pi] is a root of (Aqx+Bq[sqrt]2 - p)(Aqx-Bq[sqrt]2 - p) (a polynomial with integer coefficients)
=> [pi] is not transcendental
=> contradiction
|
| « Last Edit: Oct 15th, 2003, 10:19pm by Rezyk » |
IP Logged |
|
|
|
Rezyk
Junior Member
Gender:
Posts: 85
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #3 on: Oct 15th, 2003, 10:38pm » |
Quote Modify
|
My initial thought is to try and use the values of cos(2A[sqrt]2)=cos(2X) and cos(2[sqrt]2) to determine |A| somehow.
|
| « Last Edit: Oct 15th, 2003, 11:32pm by Rezyk » |
IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #4 on: Oct 16th, 2003, 2:06am » |
Quote Modify
|
on Oct 15th, 2003, 9:19pm, william wu wrote:| Is it true that for any [epsilon] > 0, [exists] integers A and B such that [epsilon] = A[pi] + B[sqrt]2? How to prove/disprove this? |
|
We can disprove this, and deduce something about [epsilon] in the process...
::
Suppose that [epsilon] is algebraic.
[epsilon]–B[sqrt]2=A[pi].
LHS is be algebraic, but RHS is transcendental.
Hence [epsilon] cannot be algebraic.
Futhermore, we can now assert that [epsilon] must be transcendental.
::
I've not solved it yet, but this is a really interesting problem...
::
The result follows from solving, tan(X)=tan(A[sqrt]2) (or cosine).
Therefore, X=A[sqrt]2+B[pi].
We seem to be dealing with a type of periodic equivalence with transendentals over an infinite domain, but with a particular solution. I'm suspecting that we can do something with Euler's formula. By working with a complex domain we might be able to make more progress with this problem?
::
|
|
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #5 on: Oct 16th, 2003, 5:18pm » |
Quote Modify
|
My first thought was that any x that meets the conditions and can be well defined would have to be written in a form such that the values of A and B are immediately obvious. x is transcendental (unless B=0) so it is not easily described without giving away the integer coefficient of [pi].
However, try finding A and B when x is given by this rapidly converging series (remember brute force is discouraged):
|
|
IP Logged |
|
|
|
James Fingas
Uberpuzzler
Gender:
Posts: 949
|
Here are my thoughts about this problem.
First of all, it is quickly apparent that any real number can be approximated to arbitrary precision with a number of the form X = A[sqrt]2 + B[pi].
This presents the obvious problem that, without infinite-precision arithmetic, we cannot be sure that we have arrived at the actual solution, or have arrived at a very good approximation of a solution.
Infinite-precision arithmetic presents a difficult task. The only real alternative is to restrict our analysis to numbers such as the one that SWF gives in the preceding post. This is interesting, and I'm sure it's difficult, but does not bode well for this being a general sort of question.
So what can we do with finite precision arithmetic? Quite a lot, actually. Take an arithmetic with a precision of [epsilon] (the granularity of the numbers used). Assume that all calculations, including computing X = A[sqrt]2 + B[pi], can be done to an accuracy of [epsilon]. I know this is a bad simplification, and I'm sure we could come up with something better, but it would be markedly more complex.
Now we define p, the confidence we want to have in our answers. I'll use p=0.001 here. By choosing p in this way, we make sure that when we find candidate A and B that could make up X, we know with 99.9% confidence that X is actually a number formed by X = A[sqrt]2 + B[pi], rather than just a random number.
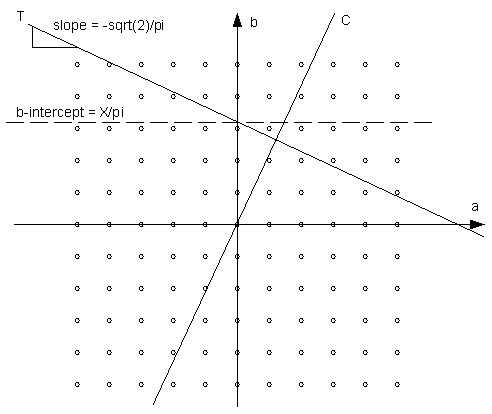
The model I define for the problem is that we are searching the grid of numbers (a,b) for pairs that are close to the line X = a[sqrt]2 + b[pi], or b = -a[sqrt]2/[pi] + X/[pi] (call this line 'T' for target). The constraint that we will put on these values of (a,b) is that they are also as close to (0,0) as reasonably possible. That means we will try to minimize the absolute value of a - b[sqrt]2/[pi] (which is the perpendicular to the line T that passes through the origin). Call the line a - b[sqrt]2/[pi] = 0 'C' for constraint. See the diagram below.
How do we do this for an arbitrary X (given to a precision of [epsilon])? I'll let you think about that one, but once we have picked a pair (a,b) that is as close to the line T as possible without being more than M away from the line C (M is found while solving this problem, and is roughly p/[epsilon]), we can check to see if the number we were given was based on a particular pair (c,d), or whether it was just a random number with no "reasonable" solution, with a probability of error of p=0.001.
|
|
IP Logged |
Doc, I'm addicted to advice! What should I do?
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #7 on: Oct 17th, 2003, 5:09pm » |
Quote Modify
|
Here is another x that can also be written as A[sqrt]2+B[pi]:
|
|
IP Logged |
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2873
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #8 on: Oct 19th, 2003, 7:25pm » |
Quote Modify
|
A quick quibble about some of the arguments being thrown around ::[epsilon] can be algebraic for a small (countably infinite) number of cases - those where the coefficient of [pi] is 0::
Not that I have anything useful to contribute
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #9 on: Oct 19th, 2003, 8:36pm » |
Quote Modify
|
A different, simpler, proof that numbers of the form (A[sqrt]2 + B[pi]) do not consist of all positive reals is simply to note that the set of such numbers is countable, while the positive reals are not.
My thought is to find an integer B satisfying
x[sup2] - 2B[pi]x + B[sup2][pi][sup2] [equiv] 0 mod 1. I may be wrong, but I suspect that if such a B exists, it has to be unique.
|
| « Last Edit: Oct 20th, 2003, 9:44am by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #10 on: Oct 20th, 2003, 12:42am » |
Quote Modify
|
on Oct 19th, 2003, 8:36pm, Icarus wrote:My thought is to find an integer B satisfying
x[sup2] - 2Bx + B[sup2][pi][sup2] [equiv] 0 mod 1. I may be wrong, but I suspect that if such a B exists, it has to be unique. |
|
Isn't there a [pi] missing there? It seems to me it should be x[sup2] - 2B[pi]x + B[sup2][pi][sup2] [equiv] 0 mod 1
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #11 on: Oct 20th, 2003, 9:46am » |
Quote Modify
|
Look again - there is a second [pi] in there. And please ignore the edit announcement at the bottom. It has nothing to do with this. Honest - it doesn't! 
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #13 on: Oct 21st, 2003, 8:41am » |
Quote Modify
|
Teehee, we could have great fun with this...
Suppose that I quote you after making a mistake:
on Oct 20th, 2003, 11:10am, towr wrote:you forgot to edit my quote  |
|
I then edit this post for no good reason.
You go back to correct your post, and hopefully post a follow up to acknowledge that you have changed it.
The trap has been sprung. I couldn't have misquoted a virgin post (one without the edit tell-tale sign below it), but now...
I can re-edit my post and change it to something like below (adding the [e] [/e] below to make it look like I've been back for a good reason):
on Oct 20th, 2003, 11:10am, towr wrote:| you forgot to edit my quote – by the way, I've finally decided to bow to Sir Col's mighty intellect and accept that the natural numbers are 1,2,3,... (not including zero). Sorry for doubting your magnificance! |
|
[e]Ooh, I forgot to thank you before for your kind words[/e]
|
| « Last Edit: Oct 21st, 2003, 8:47am by Sir Col » |
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #14 on: Oct 21st, 2003, 9:03am » |
Quote Modify
|
on Oct 21st, 2003, 8:41am, Sir Col wrote:| Teehee, we could have great fun with this... |
|
Espescially as moderators
Quote:| I can re-edit my post and change it to something like below (adding the [e] [/e] below to make it look like I've been back for a good reason): |
|
Well, of course any quotes in an edited post are somewhat suspect. Even when they aren't misquotes.. 
Good thing we're all fairly honest around here..
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #15 on: Oct 27th, 2003, 6:51pm » |
Quote Modify
|
I thought I should give the answers to the the two equations I gave above in case I lose my notes and the solution goes the way of Fermat's proof.
The first equation I gave equals: (-192)*[surd]2+(96)*[pi] and was found by using the series for sin([pi]/4) =[surd]2/2 and choosing coefficients to make the coefficient of [pi]1 be zero.
The equation in my second post equals: (-4)*[surd]2+(2)*[pi] and was found by using the series for sin-1([surd]2/2)=[pi]/4 and choosing coefficients that make the coefficient of [surd]2 be zero.
|
| « Last Edit: Oct 27th, 2003, 7:36pm by SWF » |
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #16 on: Oct 27th, 2003, 7:06pm » |
Quote Modify
|
My apologies for messing with your post, SWF, but I found the combination of hidden numbers that need to be highlighted to be seen and unhidden symbols that do not show at all when highlighted made the post extremely difficult to read.
Anyone who is reading this far down in the thread is not looking for hints, but rather has been highlighting and reading the previous posts anyway. In my opinion, late in the thread hiding text becomes more of a nuisance than it's worth.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #17 on: Oct 27th, 2003, 7:44pm » |
Quote Modify
|
No problem. I dislike trying to read hidden answers too, but when an answer is given without hiding there are often complaints. It would be my pleasure to cut back on inserting those tags in so much.
|
|
IP Logged |
|
|
|
Sir Col
Uberpuzzler
impudens simia et macrologus profundus fabulae
Gender:
Posts: 1825
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #18 on: Oct 28th, 2003, 6:03am » |
Quote Modify
|
on Oct 27th, 2003, 7:06pm, Icarus wrote:| In my opinion, late in the thread hiding text becomes more of a nuisance than it's worth. |
|
I'm glad someone else feels this way. It'd be good to have some clarity or other peoples thoughts on this issue. When to hide, when not to hide? Maybe you could start a poll, to canvas opinion, in more common location?
I appreciate that posting the 'answer' below the first post (containing the question), is not good. But once we get into discussing the solutions and presenting support and refutations, do we need to hide these posts? It is frustrating to have to continuously highlight the text and there is a definite issue with the symbols: they're visible when hidden, and often invisible when highlighted.
|
| « Last Edit: Oct 28th, 2003, 6:04am by Sir Col » |
IP Logged |
mathschallenge.net / projecteuler.net
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #19 on: Oct 28th, 2003, 6:21am » |
Quote Modify
|
The symbols things is indeed annoying. I tend not to use them anymore when I intend to hide the text they're in, and just use sqrt() and whatever else we used before we had the symbols.
Perhaps it would help if we had a different kind of hiding system, one were you don't highlight the text, but just push a button or something. This is simple to do by just changing the style from visible to invisible with javascript. It has the added benefit that it works on images as well (just put it in a div-element, and hid the whole thing untill someone unhides it by pushing the 'unhide'-button)
The current system could be overlaid as consideration to those who don't like javascript and have it disabled (or have archaic browsers that can't read it)
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Brian
Guest
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #20 on: Nov 11th, 2003, 9:12pm » |
Quote Modify
 Remove
|
Why not use integer relation algorithms (via standard lattice reduction methods)?
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #21 on: Nov 12th, 2003, 6:08pm » |
Quote Modify
|
Because jargon alone fails to impress the ladies. Care to elaborate?
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Brian
Guest
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #22 on: Nov 13th, 2003, 8:17am » |
Quote Modify
Remove
|
You are given a basis Pi and Sqrt[2]. You want to find A and B such that A Pi + B Sqrt[2] is closest to the given number X. This is an entirely standard problem in the theory of lattices. It is also NP-complete, in general. Luckily, we have very good approximation algorithms (LLL and BKZ, principally). There are some tricks to makes sure that the algorithm is numerically stable and convergent in a reasonable amount of time. Typically, 30 digits of precision will be able to pin down A and B if they are in the range of ~10^6 or less. Victor Shoup's NTL library has perhaps the nicest free implementation of LLL, combined with excellent arbitrary precision integer arithmetic support.
|
|
IP Logged |
|
|
|
Michael Dagg
Guest
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #23 on: Apr 13th, 2005, 7:35pm » |
Quote Modify
Remove
|
on Oct 15th, 2003, 9:06pm, william wu wrote:Say I am given a number X = A*[sqrt]2 + B*[pi], where A and B are integers.
Given X, how can you find A and B, without using brute force? |
|
This is one of the more interesting discussions. But, unfortunately it cannot be done.
While it is clearly possible to find A and B such that A*sqrt(2) + B*pi is within some epsilon of X, this is a different problem all together than what Mr. Wu stated and is certainly not strongly NP-complete, since we can find A and B within some deterministic time by truncating X and achieving the same epsilon radius for the same A and B. Try it.
There is a Fresnel integral for sqrt(pi) that contains sqrt(2) as a factor and looks like
sqrt(pi) = 2*sqrt(2)*int[cos(z^2) dz, lower=0, upper=infinity]
that can be used to manipulate the original expression involving pi into an integral expression without pi. However, after a great deal of messy work you will eventually end up with an expression with some terms that are nonsense.
The fundamental reason it cannot be done is stated in Icarus's post: the set {A*sqrt(2)+B*pi: A,B in Z} is countable whereas the set {X: X in R} is uncountable.
Regards,
MD
|
|
IP Logged |
|
|
|
Deedlit
Senior Riddler
Posts: 476
|
|
Re: Combinations of Pi and Sqrt(2)
« Reply #24 on: Apr 13th, 2005, 10:12pm » |
Quote Modify
|
I think William was talking just about X that is actually expressible in that form. But it does seem like you can't do much without any restriction on how X is presented. It reminds me a little of the word problem in group theory - given a finitely presented group, is there always an algorithm for determining when a word equals the identity? The surprising answer is that you can't.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print