Author |
Topic: Topological Rings (Read 14712 times) |
|
william wu
wu::riddles Administrator
Gender: 
Posts: 1291
|
 |
Topological Rings
« on: Feb 3rd, 2003, 1:34pm » |
 Quote  Modify
|
TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS TOPOLOGICAL RINGS
A real nice puzzle. My favorite kind: people of all ages can understand that it seems totally impossible 
 
Imagine the object above in the figure to the left made from perfectly elastic material. Can you transform it so as to unlink the two rings as in the figure on the right? One possible way is to cut one ring, move the other ring through the gap, and rejoin the the first ring exactly as it was. That would be a legitimate topological transformation. However, it is also possible to transform the first shape into the second without any cutting, simply by manipulating the objects in the appropriate manner (stretching, bending, but not breaking). Can you see how to do it?
Note: Source: Brandon McPhail. Play his spiffy set applet at http://www.reed.edu/~mcphailb/applets/set
|
| « Last Edit: Feb 3rd, 2003, 3:30pm by william wu » |
 IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Chronos
Full Member
Gender:
Posts: 288
|
|
Re: Topological Rings
« Reply #1 on: Feb 3rd, 2003, 4:57pm » |
Quote Modify
|
OK, I think I've figured out, but I'ven't a clue how one might try to express the answer, without some sort of 3D drawing tools.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #2 on: Feb 3rd, 2003, 7:34pm » |
Quote Modify
|
One solution came to mind almost immediately, but I'm not sure it is the one you are looking for. To find out, I will ask this hidden question:
Is the inverse transformation also continuous? The one I thought of isn't.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Topological Rings
« Reply #3 on: Feb 3rd, 2003, 8:22pm » |
Quote Modify
|
This is interesting. It looked impossible at first, but after finding a good way to visualize, it seems almost obvious. I can give a fairly brief and clear written description that I believe would make it pretty clear to most people. This problem is too good give away so soon, so I will generously let everyone enjoy the problem.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #4 on: Feb 3rd, 2003, 8:34pm » |
Quote Modify
|
I have it! Just push a section of one of the rings in the direction of a 4th spacial dimension! You can then bring the other ring out in that area, and pull the first ring back into 3 dimensions again. So easy, anyone can do it! 
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Kozo Morimoto
Junior Member
Posts: 114
|
|
Re: Topological Rings
« Reply #5 on: Feb 5th, 2003, 4:37pm » |
Quote Modify
|
Are you allowed to join? (like playdoe)
|
|
IP Logged |
|
|
|
aero_guy
Senior Riddler
Gender:
Posts: 513
|
|
Re: Topological Rings
« Reply #6 on: Feb 5th, 2003, 10:28pm » |
Quote Modify
|
I have a solution, but it isn't a 'eureka' solution. So I will ask:
is perspective key?
|
|
IP Logged |
|
|
|
Chronos
Full Member
Gender:
Posts: 288
|
|
Re: Topological Rings
« Reply #7 on: Feb 6th, 2003, 11:39am » |
Quote Modify
|
aero_guy, to (hopefully) answer your question: The solution which I found does not depend on any feature of the objects which is not immediately apparent. They're just like how they look. My solution also does not rely on any more than the usual three spatial dimensions, and I actually found the inverse transformation first. I'm not sure how one transformation could be continuous without the other being so.
A minor hint, by the way:The solution is easier to see if the center section (the part not on any loop) is shorter. Since we're allowed to stretch and squish as much as we'd like, start by squishing the middle.
|
|
IP Logged |
|
|
|
Phil
Newbie
Posts: 38
|
|
Re: Topological Rings
« Reply #8 on: Feb 6th, 2003, 12:27pm » |
Quote Modify
|
I got it from your hint, I think.
Shrink the connecting bar down to nothing, and you simply have two rings joined at one point, not intertwined, just connected. Just turn the inner ring out before restretching the connecting bar.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #9 on: Feb 6th, 2003, 7:03pm » |
Quote Modify
|
on Feb 6th, 2003, 11:39am, Chronos wrote:| I'm not sure how one transformation could be continuous without the other being so. |
|
overlap the two intertwined loops and merge them into a single loop (like play-doe). The two loops on the left form a single loop on the right. The mid-section on the left forms the other loop on the right. The mid section on the right is formed by stretching out the intersection. This is a continuous transformation, but it does not have a continuous inverse, since the inverse would involve tearing apart what was joined together, which would be heresy! 
Matthew 19:6 - "What God has joined together, let no man separate."
Needless to say, your solution is much better, not to mention safer for our immortal souls! 
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
SWF
Uberpuzzler
Posts: 879
|
|
Re: Topological Rings
« Reply #10 on: Feb 6th, 2003, 8:16pm » |
Quote Modify
|
Here is how I visualize this (hidden text):
Imagine two metal hoops that are not linked. Bring them together so they almost touch at a single point. Put a drop of rubber cement at that point to join them together. This is the topological equivalent of a figure-8. If you pull the rings apart so the rubber cement stretches you get two unlinked loops joined together by a long connection as shown in the 2nd picture.
Repeat, but this time start with two linked metal hoops with a drop of rubber cement bonding them at a point. Again, it is equivalent to a figure-8, so it is same as the first case. Separate the rings as far as you can to stretch the cement, then grab the rubber cement and stretch it into a long strand. This leaves two linked rings joined by a long connection, as show in the first picture.
It may not be obvious to everyone that both cases are equivalent to a figure-8. If that is a problem, perhaps it would help to imagine the drop of cement to be a large blob of rubber cement than covers enough of the rings near the contact point so that one cannot see whether the rings are linked or unlinked.
|
|
IP Logged |
|
|
|
James Fingas
Uberpuzzler
Gender:
Posts: 949
|
|
Re: Topological Rings
« Reply #11 on: Feb 7th, 2003, 11:35am » |
Quote Modify
|
Quote:overlap the two intertwined loops and merge them into a single loop ... the inverse would involve tearing apart what was joined together, which would be heresy!
Matthew 19:6 - "What God has joined together, let no man separate." |
|
Heresy? Pronouncing that you are God--now that's heresy!
|
|
IP Logged |
Doc, I'm addicted to advice! What should I do?
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #12 on: Feb 7th, 2003, 9:18pm » |
Quote Modify
|
Aye - but that heresy is an old tradition in my family! (Google for "sinclair Templar Jesus" if you want to know - but you'd be wise not to! )
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Guest
Guest
|
Does this mean there is no actual solution to this problem? That is, if you have a stretchable rubber pipe which has been formed into the configuration in the first figure, is there no way you can manipulate it to unlink the rings?
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #14 on: Nov 22nd, 2003, 12:39pm » |
Quote Modify
|
No - it has a solution. Chronos and Phil have described one way of looking at it (the descriptions are hidden - highlight their posts to read them).
Note though that describing the material a being like rubber is not quite the right idea. The rings are to be considered as made of "topological clay", which can be deformed freely (streched, compressed, twisted, pulled along itself, etc) without any resistance, but can never be cut or torn.
An alternative - but equivalent - description to the one offered by Chronos and Phil is: Think of the loops as being made from a "rope" of the material, with the ends of the rope looping back to attach to points in the middle. Because of the deformation properties, we can move these attachment points in a continuous fashion. So, move one of the attachments up until it moves past the other attachment, so that the one loop reattaches in the middle of the other loop. Now move the attachment in a 360o trip around the diameter of the rope there - this unlinks (if you go in the right direction) the two loops. Finally you migrate your attachment point back down to where it started from.
This is a bit hard to explain in words, but it is actually fairly simple. If this is too confusing a description, I'll try to exercise my poor artistic talents to produce recognizable pictures.
|
| « Last Edit: Nov 24th, 2003, 3:21pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
rmsgrey
Uberpuzzler
    
Gender:
Posts: 2874
|
|
Re: Topological Rings
« Reply #15 on: Nov 22nd, 2003, 5:24pm » |
Quote Modify
|
My visualisation is:
::
Imagine inflating the center section like a balloon to get a sphere with a couple of linked "handles" - the attachment points of which can float around on the surface of the sphere, but can't touch each other. It's then much easier (IMO) to visualise moving one end of one handle round an end of the other handle to unwind them. If you then let the sphere deflate back down to the original center section you get the second object
::
And a quick quibble: making the object of perfectly elastic material would be counterproductive since, as soon as you let go of it, it would return to its original form. Making it of perfectly plastic material would allow you to exhibit the object in the terminal states as well as in any intermediate state you wish.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #16 on: Nov 22nd, 2003, 5:57pm » |
Quote Modify
|
Yes - that is a much more easily described solution than mine. (It is not a better solution than mine or Chronos or Phil's since all the solutions are equivalent, but it is certainly easier to see from your description than mine is.)
And "plastic" is indeed the correct word. The only problem with it is that people are not nearly as aquainted with the meaning of it as used here, as they are with using it to refer to a family of materials (which are given the name because most of them exhibit a high plasticity).
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
They say a picture is worth a thousand words. Everyone knows that I am a fan of the thousand words, but here is a picture of what I was trying to describe anyway. As you can see, I am also a great artistic talent.
|
|
IP Logged |
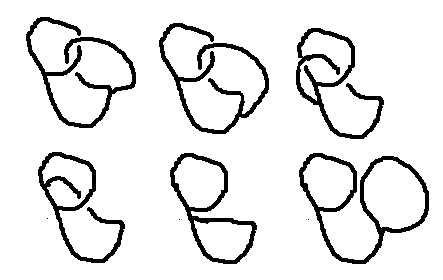
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Guest
Guest
|
No no, that is okay. I do understand the two solutions. I wanted to know if it is possible to do it without going into the stretching and compressing stuff. I think there are some configurations which seem equally impossible but can be solved ( not using the ideal compression and stretching used in this problem). I was wondering if such a solution exists for this problem.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #19 on: Nov 23rd, 2003, 6:17pm » |
Quote Modify
|
I'm not even sure what sort of a puzzle you have without the "stretching and compressing stuff". This is a topology problem from the study of knots and links, which is itself a part of homotopy theory. The stretching and compressing are just a "layman" description of homotopy.
Without stretching or compressing or cutting or joining, then no - you cannot unlink them in 3D space. (You can in 4D.)
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
SWF
Uberpuzzler
Posts: 879
|
Guest, you could try and reproduce these manipulations with an equivalent shape made of flexible material like a pair of shorts, but you are not going to get the leg holes to link together.
The shape in the puzzle is a single shape with two holes in it, so I would not say there are two rings that become linked and unlinked. If you paint two unlinked circles anywhere on the surface of the object, those circles will remain unlinked.
The figure below shows what I previously described. On the left is an 8 shape. It is all one object, but is colored for descriptive purposes. The green and blue remain rigid and are almost complete rings. They join at a blob of stretchy material which I made the same color as Silly Putty. If you pull apart as the picture on the lower right it looks like two unlinked rings joined by a bridge of Silly Putty. If you twist the rings relative to one another and push together as shown on the top right, they look like they are linked.
Also shown is what happens if you paint a red circle around the inside of the blue ring. When deformed to form the "linked" configuration the new shape of the red paint is shown (with the dotted lines being behind the putty). From that it is seen that the red line never links with the green circle, but goes around the outside of it. It is more natural to assume the red line goes straight across the putty to close the blue ring, which causes one to think rings have become linked.
If you tried this with a non-stretchy but flexible object, the deformation required of the red line (and the comparable line on the green ring) would become apparent. For example, with something made of fabric, the perimeters of the holes would never link, but you could fold them in the path of the red line.
|
|
IP Logged |
|
|
|
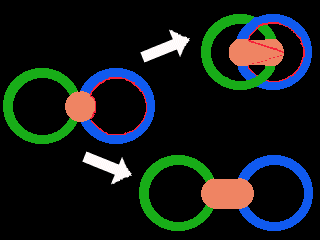
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #21 on: Nov 24th, 2003, 3:23pm » |
Quote Modify
|
Okay, I see what you meant now. I didn't get the right picture in my mind from reading your original post. I've removed the offending sentence! 
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Guest
Guest
|
Thanks a lot. Further, does this topological equivalence of the two shapes have any significance somewhere in physics or other sciences? Or is it just a beautiful mathematical result?
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: Topological Rings
« Reply #23 on: Nov 27th, 2003, 9:53pm » |
Quote Modify
|
This particular equivalence is rather doubtful. But more generally, homotopy has application in particle theory, and more specifically, the theory of links has applications in string theory (don't ask what they are - I never got that far into it).
I suspect that other applications exist as well.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
LZJ
Junior Member
Gender:
Posts: 82
|
|
Re: Topological Rings
« Reply #24 on: Nov 27th, 2003, 11:07pm » |
Quote Modify
|
For applications in string theory, I seem to recall the theory of links coming in when considering the possible ways in which superstrings join together...can't be sure though.
|
|
IP Logged |
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print
Remove