Author |
Topic: The bacterium (Read 12828 times) |
|
Wah
Newbie
Gender: 
Posts: 5
|
 |
The bacterium
« on: Jan 21st, 2003, 9:27pm » |
 Quote  Modify
|
A bacterium splits into two identical ones with probability p, otherwise it dies. What is the probability that, beginning with this one bacterium, the colony lasts forever? 
|
|
 IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: The bacterium
« Reply #1 on: Jan 21st, 2003, 11:53pm » |
Quote Modify
|
interesting puzzle..
I have no idea on how to solve it..
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: The bacterium
« Reply #2 on: Jan 22nd, 2003, 1:15am » |
Quote Modify
|
My almost complete solution below -- i invite someone else to finish it -- using the newly implemented hide tags:
To make things easier to think about for me, I will compute the probability that the colony becomes extinct. Then the probability of immortality = 1 - probability of extinction. Denote the probability of extinction by s.
A 1st generation: the very first bacterium
/ \
B C 2nd generation: two kids
Denote the first bacterium by A. A can make either 0 or 2 kids for the next generation. These are disjoint events, so from the total probabiility theorem (which basically just adds up all possible cases that can create a desired result):
s = (prob. A dies) + (prob. A splits)*(prob. A's kids have immortal family trees | prob. A splits)
s = (1-p) + p*s2
Reasoning: In the case where A makes 0 kids, the colony is dead from the start. This happens with probability 1-p, since it is the complementary event to the first bacterium splitting. Then we have an addition sign, because we wish to consider a completely disjoint event where A has 2 kids. (Formally said, given two events E and F, Pr(E OR F) = Pr(E) + Pr(F) if Pr(E AND F) = 0.) Note that the colony will now become extinct only if BOTH family trees created by A's kids become extinct. Now for the somewhat clever part, I claim this extinction probability, given that A splitted, is s2. This can be deduced from two facts:
1) The probability distribution of offspring for a single bacterium is identical across all generations. That is, if we denote X as a random variable returning the number of kids a bacterium has, then
P(X = 2) = p
P(X = 0) = 1-p
P(X = anything else) = 0
regardless of where in history the bacterium is. Thus you would expect the prob. of extinction for B's tree = prob. of extinction for C's tree = prob. of extinction for A's tree = s.
2) The trees produced by B and C develop independently of each other. Thus the probability that B's tree becomes extinct AND C's tree becomes extinct = probability that B's tree becomes extinct * probability that C's tree becomes extinct. (When you have two independent events, the probability of their intersection is the product of the individual probabilities.)
If you're convinced, now all we have to do is solve our quadratic equation for s!
s = (1-p) + p*s2
0 = p*s2 - s + (1-p)
refresher: roots of quadr = { -b +/- sqrt(b2 - 4ac) } / (2a)
Plugging stuff in gives us two possible solutions for s (you can verify it yourself)
s = 1, or
s = (1-p) / p
How do you know which value for s is valid? I'll let someone else finish this up.
|
| « Last Edit: Jan 22nd, 2003, 1:19am by william wu » |
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
Wah
Newbie
Gender:
Posts: 5
|
|
Re: The bacterium
« Reply #3 on: Jan 22nd, 2003, 5:55am » |
Quote Modify
|
that was definitely a clever answer. 
|
|
IP Logged |
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: The bacterium
« Reply #4 on: Jan 22nd, 2003, 8:54am » |
Quote Modify
|
quite a clever solution.. I wish I thought of it :p
on Jan 22nd, 2003, 1:15am, william wu wrote:
How do you know which value for s is valid? I'll let someone else finish this up.
|
|
well, if you take p = 0.2, then s would be 4 in the latter case, and s has to be between 0 and 1, so only the other option is left..
On the other hand if p=1, then the colony obviously will survive.. so the former doesn't work out really..
[note]the hide tags don't work when quoted[/note]
|
| « Last Edit: Jan 22nd, 2003, 9:00am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
BNC
Uberpuzzler
Gender:
Posts: 1732
|
|
Re: The bacterium
« Reply #5 on: Jan 22nd, 2003, 9:41am » |
Quote Modify
|
To follow up on towr an WW:
If p<0.5, s=1 and the bacteria colony is doomed.
If p>0.5, s=1/p-1, and the colony has a fair shot.
p=0.5 yield the same result for both solutions, and is the border case.
|
| « Last Edit: Jan 22nd, 2003, 9:41am by BNC » |
IP Logged |
How about supercalifragilisticexpialidociouspuzzler [Towr, 2007]
|
|
|
william wu
wu::riddles Administrator
Gender:
Posts: 1291
|
|
Re: The bacterium
« Reply #6 on: Jan 22nd, 2003, 10:01am » |
Quote Modify
|
So in general, if the number of kids a bacterium has is given by the random variable X, and the probability that a bacterium has k kids is given by the distribution P(X = k), what property should this distribution have to ensure that the colony propagates forever? Also, when does the border case ensure immortality?
|
|
IP Logged |
[ wu ] : http://wuriddles.com / http://forums.wuriddles.com
|
|
|
BNC
Uberpuzzler
Gender:
Posts: 1732
|
|
Re: The bacterium
« Reply #7 on: Jan 22nd, 2003, 10:39am » |
Quote Modify
|
These type of problems are solved using Markov chains. This riddle, nice and hard as it is, is but a simple case. Real-life scenarios (birth-probability, death-probability, migration probability, over-crowding) are much more difficult.
|
|
IP Logged |
How about supercalifragilisticexpialidociouspuzzler [Towr, 2007]
|
|
|
Wah
Newbie
Gender:
Posts: 5
|
|
Re: The bacterium
« Reply #8 on: Jan 23rd, 2003, 4:13am » |
Quote Modify
|
i am convinced about the above solution
but one of my friend cam up with the folowing and i can't see the flaw in it
here it goes:
"Chance of 1 bacteria splitting = p
Chance of 1 bacteria dieing = 1 - p
If p occurs, number of bacteria "n" = n + 1
If 1 - p occurs, number of bacteria "n" = n - 1
At any given point in time, the colony will have n bacteria in it. The chance of ALL bacteria splitting is p to the power n. The chance of ALL bacteria dieing is (1-p) to the power n. All other results will result in a change in the value of n, because as long as at least ONE bacteria splits, the colony will exist for the next stage of splitting.
Therefore, in order for the bacteria colony to exist, at least ONE bacteria must split at each stage of multiplication, because if it doesn't, then that means that all bacteria have died.
The probability of AT LEAST ONE bacteria splitting is equal to 1 - the probability of all bacteria dieing, which is:
1 - ( ( 1 - p ) to the power n )
In order for a colony to exist forever, then this event needs to occur EVERY SINGLE TIME. n is variable based on what the value of n was last time.
so the probability of the colony existing after 3 multiplications is:
(1-((1-p)^n1)) * (1-((1-p)^n2)) * (1-((1-p)^n3))
In order for the colony to exist forever, then this needs to go on for infinity: (1-((1-p)^n1)) * (1-((1-p)^n2)) *. . . * (1-((1-p)^ninfinity))
Because n is always a positive whole number >1 , it means that each one of these expressions will ALWAYS be LESS than one.
So what your saying is you have an INFINITE number of numbers less than one which you are multiplying together.
Which is 1/infinity.
So the probability of a colony existing FOREVER is 1/infinity.
Which, in my book, is ZERO. "
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: The bacterium
« Reply #9 on: Jan 23rd, 2003, 6:57pm » |
Quote Modify
|
If you could show that the multiplicands in your product are bounded away from 1, then you can claim rightly that the limit is zero. But in fact if the exponents climb, the multiplicands converge to 1, which allows the product to converge to a limit greater than zero.
Here is an example of an infinite product of numbers less than one that converges to a non-zero result:
(Thanks, towr, for this great formula generator!)
If you can't see the formula, here it is using the new math symbolry:
[prod]n=0[supinfty] 2-2[supminus][supn] = 1/4
|
| « Last Edit: Nov 3rd, 2003, 6:12pm by Icarus » |
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
Chronos
Full Member
Gender:
Posts: 288
|
|
Re: The bacterium
« Reply #11 on: Feb 3rd, 2003, 5:34pm » |
Quote Modify
|
But in any event, you certainly can't guarantee immortality unless p=1. If p is less than 1 by any amount, then there's a nonzero chance of the "colony" dying off rightat the outset, before any reproduction has occured.
|
|
IP Logged |
|
|
|
NickH
Senior Riddler
Gender:
Posts: 341
|
 |
Re: The bacterium
« Reply #12 on: Feb 9th, 2003, 8:38pm » |
Quote Modify
|
Here's another approach.
Let Pn be the probability that n bacteria will eventually become extinct. By independence, Pn = P1n.
The probability of the colony becoming extinct after the first split is (P0 + P2)/2. But this is just P1.
Setting P1 = p, we have p = (1 + p2)/2, from which p = 1.
So the colony survives indefinitely with probability 0.
Of course, we should get the same answer if we allow each bacterium three (equally likely) choices: die, do nothing, or split in two. And indeed we then have p = (1 + p + p2)/3, which again yields p = 1.
Suppose now we allow the bacterium a different three choices: die, split in two, or split in three. Then p = (1 + p2 + p3)/3, from which p = 1 or p = sqrt(2) - 1. I believe the latter is the correct answer, but how can we justify excluding p = 1?
|
|
IP Logged |
Nick's Mathematical Puzzles
|
|
|
James Fingas
Uberpuzzler
Gender:
Posts: 949
|
|
Re: The bacterium
« Reply #13 on: Feb 10th, 2003, 11:42am » |
Quote Modify
|
NickH,
I don't agree.
Quote:| The probability of the colony becoming extinct after the first split is (P0 + P2)/2. But this is just P1. |
|
From what I understand, you are say: "with probability 0.5, the colony dies the first step, and with probability 0.5, it turns into a colony of size 2, with probability of dying of surviving P2"
The problem with this is that it doesn't always die with probability 0.5 in the first step. The original problem statement calls the probability of it dying on the first step (1-p), but that won't work with your assignment of p, so let's call this probability q. Then:
Therefore, P1 = (1-q)P2 + qP0 = p2(1-q) + q
In other words, we can find q in terms of p, but we can't directly find p by this method. But, when you consider that all we wanted to do was to find p in terms of q, then you have solved the problem in a very simple way! (although it is the same solution that William posted)
I don't agree that the probability of the colony surviving is always 0. Take a look at the "simple game" thread; I think you'll notice a lot of similarities to this problem.
http://www.ocf.berkeley.edu/~wwu/cgi-bin/yabb/YaBB.cgi?board=riddles_har d;action=display;num=1028570694
|
|
IP Logged |
Doc, I'm addicted to advice! What should I do?
|
|
|
NickH
Senior Riddler
Gender:
Posts: 341
|
|
Re: The bacterium
« Reply #14 on: Feb 10th, 2003, 3:33pm » |
Quote Modify
|
James,
You're right, of course. I misread the question and ended up answering a different (though interesting) one! Scratch the above post.
Nick
|
|
IP Logged |
Nick's Mathematical Puzzles
|
|
|
Eigenray
wu::riddles Moderator
Uberpuzzler
Gender:
Posts: 1948
|
|
Re: The bacterium
« Reply #15 on: Nov 3rd, 2003, 5:43am » |
Quote Modify
|
To prove convergence, let pn be the probability that the bacteria have died out by n generations. We're interested in the limit of pn as n goes to infinity. Note that pn is increasing, and bounded above, so it must converge. Also, the probability of k bacteria all dying out after n generations is simply pnk. Therefore:
p1 = 1-p
pn+1 = 1-p + p pn2.
Since pn converges, it must converge to a fixed point of the map f(x) = 1 - p + px2.
This map has two fixed points, 1 and (1-p)/p.
For 0<x<1, we have x < f(x) = 1-p(1-x^2) < 1, so that the limit of the pn can't exceed 1.
When p <= 1/2, (1-p)/p >= 1, so they converge to 1.
If p > 1/2, and p1 <= x < (p-1)/p, then x < f(x) < 1-p+p[(p-1)/p]2 = (1-p)/p < 1, so they must converge to (1-p)/p.
Therefore the colony survives with probability 0 when p <= 1/2, and with probability 2-1/p when p > 1/2.
|
|
IP Logged |
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: The bacterium
« Reply #16 on: Nov 3rd, 2003, 6:04pm » |
Quote Modify
|
A nice clean-up of William's solution. I don't know that convergence of pn really needed to be proven, since some simple considerations make it obvious, but as a mathematician, I have to approve!
(you better correct the typo in the last line, or else I'll have to do it).
Looking back through this thread has reminded me of a curiosity I noticed some time back involving my refutation of Wah's friend's argument. If you call up the formula examples page of towr's formula generator, you will see that while all other formulas in it rate less than 400 requests, the one I created above has over 5400. If this were some profound piece of mathematics I could understand it, but it's just a throw-out formula I cooked up to demonstrate a falacy that is also refuted by any decent low-level analysis textbook.
Towr - do you have any idea why this formula was so popular, or is this the result of some error in the page's statistics?
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: The bacterium
« Reply #17 on: Nov 4th, 2003, 12:20am » |
Quote Modify
|
on Nov 3rd, 2003, 6:04pm, Icarus wrote:| Towr - do you have any idea why this formula was so popular, or is this the result of some error in the page's statistics? |
|
I don't know, perhaps someone else on the web uses it on a page. It can't be from this thread since it's not nearly been read that many times.. Though it might occasionaly show up on a search-result page..
I don't think it's an error, but I could check and look in some of my backup-files if I can find anything..
[edit]Oh my goodness.. I think someone used it as an avatar 
At a highschool forum no less.. But I don't know who since he seems to have changed it.. (Which is why I think it was an avatar, since on most forums that completely disappears from all posts once it is changed in the profile)
After crossreferencing two threads (found in my backups), and this forum, I've come to the conclusion it was KicksGenius[/edit]
|
| « Last Edit: Nov 4th, 2003, 12:56am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: The bacterium
« Reply #18 on: Nov 4th, 2003, 9:54am » |
Quote Modify
|
That explains it! Alex is more than welcome to use it as far as I am concerned. I was just curious why it had so many hits.
And I suppose it could be considered far more profound from the point of view of a 15-year old, for whom the mathematics behind it is still something to be grasped, than it is for a 41-year old who dredged it up out of mathematics mastered before the 15-year old was born.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: The bacterium
« Reply #19 on: Nov 4th, 2003, 11:07am » |
Quote Modify
|
on Nov 4th, 2003, 9:54am, Icarus wrote:| That explains it! Alex is more than welcome to use it as far as I am concerned. I was just curious why it had so many hits. |
|
He allready stopped using it months ago, but it's an interesting avatar-choice. Most people wouldn't think to use a formula (well maybe E=mc^2)
|
|
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
ThudnBlunder
wu::riddles Moderator
Uberpuzzler
The dewdrop slides into the shining Sea
Gender:
Posts: 4489
|
Quote:| Here is an example of an infinite product of numbers less than one that converges to a non-zero result: |
|
What does this converge to?
|
|
IP Logged |
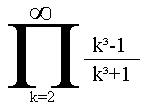
THE MEEK SHALL INHERIT THE EARTH.....................................................................er, if that's all right with the rest of you.
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: The bacterium
« Reply #21 on: Nov 4th, 2003, 12:11pm » |
Quote Modify
|
::lim n->inf - 2/(3·(n + 1)) + 2/(3·n) + 2/3 = 2/3::
|
| « Last Edit: Nov 4th, 2003, 12:12pm by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
Icarus
wu::riddles Moderator
Uberpuzzler
Boldly going where even angels fear to tread.
Gender:
Posts: 4863
|
|
Re: The bacterium
« Reply #22 on: Nov 4th, 2003, 4:54pm » |
Quote Modify
|
I must admit that my product-finding skills are rusty. The one I chose above was picked specifically to be obvious in its convergence and limit.
Proving convergence is easy (with that handy-dandy convergence theorem again: A product of {1 + un} converges iff the sum of {un} converges). In this case, uk = -2/(k3 + 1), which converges with the series {1/k3}. Since the latter series is well-known to converge, so does the product.
But so far I haven't found the method that allowed towr to produce the answer so easily.
|
|
IP Logged |
"Pi goes on and on and on ...
And e is just as cursed.
I wonder: Which is larger
When their digits are reversed? " - Anonymous
|
|
|
TimMann
Senior Riddler
Gender:
Posts: 330
|
|
Re: The bacterium
« Reply #23 on: Nov 4th, 2003, 11:10pm » |
Quote Modify
|
on Jan 22nd, 2003, 10:39am, BNC wrote:| These type of problems are solved using Markov chains. |
|
Hey, a Markov chain problem that I haven't jumped in on yet.
OK, assuming that p<1, this problem is clearly an absorbing Markov chain with only one absorbing state. That is, there is one state (0 bacteria) from which you cannot get to any other state, but it is possible (no matter how improbable) to get from any of the non-absorbing states to the absorbing state in a finite number of steps.
Therefore the process converges to the absorbing state. With probability 1, the colony eventually dies out.
(Of course the colony lasts forever if p=1, because then you can't get to the absorbing state; in fact in the number of bacteria can never decrease.)
See the reference I gave in this thread.
|
|
IP Logged |
http://tim-mann.org/
|
|
|
towr
wu::riddles Moderator
Uberpuzzler
Some people are average, some are just mean.
Gender:
Posts: 13730
|
|
Re: The bacterium
« Reply #24 on: Nov 5th, 2003, 12:51am » |
Quote Modify
|
on Nov 4th, 2003, 4:54pm, Icarus wrote:| But so far I haven't found the method that allowed towr to produce the answer so easily. |
|
I had a little help from my computer, though it needed a lot of help from my side
The main idea is splitting the product (from 2 to n) into two, and each reduces to a simple formula in terms of n, then take the limit for n to [infty]
|
| « Last Edit: Nov 5th, 2003, 1:46am by towr » |
IP Logged |
Wikipedia, Google, Mathworld, Integer sequence DB
|
|
|
|
RIDDLES SITE
WRITE MATH!
Home 
Help 
Search 
Members 
Login 
Register
Reply
Notify of replies
Send Topic
Print